Like Denominators – Definition With Examples

Denominator

A denominator is a number that is placed below the horizontal line of fraction. It is the bottom number of the fraction which shows the whole or total number of equal parts in which an object is divided. Example: In the fraction $\frac{3}{5}$, the denominator is 5. 

Kathy and Merry decided to buy a large pizza each. Kathy bought a pepperoni pizza whereas Merry bought a chicken pizza. They both decided to share the pizza. That means Kathy will give 4 slices of her pizza to Merry and Merry will give 4 slices of her pizza to Kathy. 

When they both opened the pizza, they saw that Kathy’s pizza was divided into 4 slices and Merry’s pizza was divided into 8 slices. They both got confused. Wouldn’t it be easy if the number of total slices would have been the same i.e. when the denominators would have been the same. 

What are Like Denominators?

Let us have a look at two fractions i.e., $\frac{5}{16}$ and $\frac{9}{16}$. We see that the denominators are the same i.e. 16, then the denominators are said to be like denominators. In other words, when the denominators of two or more fractions are the same, they are called like denominators. Such fractions are also called as like fractions. 

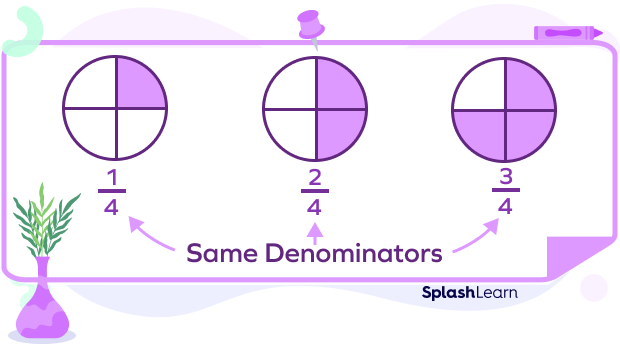
In the figure above, the denominator in all the free fractions is the same i.e. 4. So, the denominators are like denominators. 

How to Convert Denominators to Like Denominators?

We can make the denominators of two fractions like or same by finding the LCM of the denominators and then multiplying the fractions by a suitable number.

For example, consider the two fractions $\frac{1}{4}$ and $\frac{2}{10}$. 

Step 1: Since the denominators are different, we will find the LCM of 4 and 10.

LCM (4, 10) = 20

Step 2: Multiply by suitable numbers. 

$\frac{1\times5}{4\times5}$ = $\frac{5}{20}$ 

$\frac{2\times2}{10\times2}$ = $\frac{2}{20}$

The denominators are like denominators now. 

Compare Fractions with Like Denominators

Comparing fractions with like denominators is quite easy. We just compare the numerators of these fractions.

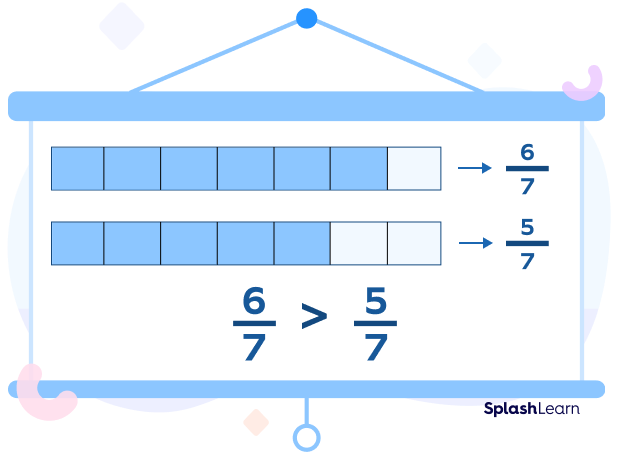
For example, we have to compare $\frac{6}{7}$ and $\frac{5}{7}$.

Since the denominators are the same, we will compare the numerators only.

6 > 5 $\Rightarrow$ 67>57 

Add Fractions with Like Denominators

It is easier to add fractions with like denominators. Let us add with an example:

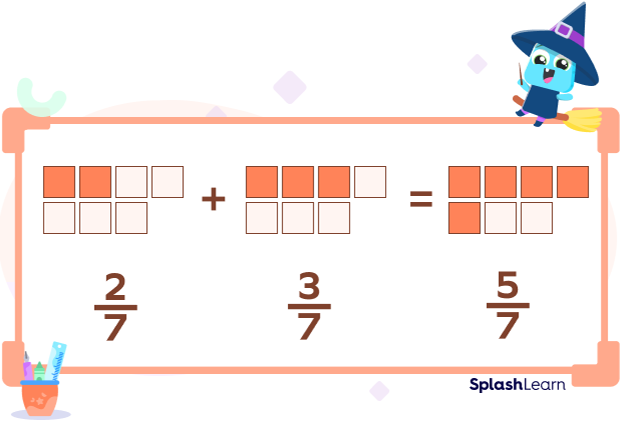
$\frac{2}{7}$ + $\frac{3}{7}$

Since the denominators are the same, we will only add the numerators. 

$\frac{2}{7}$ + $\frac{3}{7}$ = $\frac{2 + 3}{7}$ = $\frac{5}{7}$

Subtract Fractions with Like Denominators

When we subtract the fractions with like denominators, we subtract the numerators only:

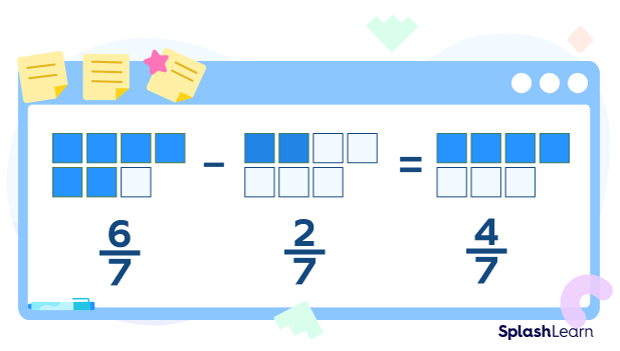
$\frac{6}{7}$ $-$ $\frac{2}{7}$

Since the denominators are the same, we will only subtract the numerators. 

$\frac{6}{7}$ $-$ $\frac{2}{7}$ = $\frac{6 – 2}{7}$ = $\frac{4}{7}$ 

Operations on Unlike Denominators

For doing operations with unlike denominators, we will first convert them into like denominators and then apply the operation on them as we used to do in the case of like denominators. 

For example, we have to compare $\frac{2}{3}$ and $\frac{3}{4}$. 

Since the denominators are unlike, we will first make the denominator like by finding the LCM.

LCM (3, 4) = 12

$\frac{2\times4}{3\times4}$ = $\frac{8}{12}$ and $\frac{3\times3}{4\times3}$ = $\frac{9}{12}$ 

Since 8 < 9 $\Rightarrow$ $\frac{8}{12}$ < $\frac{9}{12}$. 

If we have to add $\frac{2}{3}$ and $\frac{3}{4}$, we will get $\frac{8}{12}$ + $\frac{9}{12}$ = $\frac{17}{12}$ = $1\frac{5}{12}$.

If we have to subtract  $\frac{3}{4}$ and $\frac{2}{3}$, we will get $\frac{9}{12}$ $-$ $\frac{8}{12}$ = $\frac{1}{12}$.

Solved Examples

Example 1: Write $\frac{7}{16}$,$\frac{5}{16}$,$\frac{9}{16}$, and $\frac{1}{16}$ in ascending order.

Solution: Since the denominators are the same, we will compare the numerators. 

1 < 5 < 7 < 9 $\Rightarrow $$\frac{1}{16}$ < $\frac{5}{16}$ < $\frac{7}{16}$ < $\frac{9}{16}$

Example 2: Convert $\frac{3}{5}$ and $\frac{2}{7}$ into fractions with like denominators. 

Solution: LCM (5, 7) = 35

$\frac{3\times7}{5\times7}$ = $\frac{21}{35}$ and $\frac{2\times5}{7\times5}$ = $\frac{10}{35}$ 

$\frac{21}{35}$ and $\frac{10}{35}$ are fractions with like denominators. 

Example 3: Add $\frac{3}{4}$ + $\frac{7}{4}$ + $\frac{11}{4}$ and convert it into an improper fraction.

Solution: Since the denominators are same or like, we will add the numerators.

$\frac{3}{4}$ + $\frac{7}{4}$ + $\frac{11}{4}$ = $\frac{3 + 7 + 11}{4}$ = $\frac{21}{4}$ = $5\frac{1}{4}$.

Practice Problems

Frequently Asked Questions