Unlike Denominators

What Is a Denominator?

Fractions represent a part of the whole. When numbers are written as a fraction, it can be represented as $\frac{p}{q}$, where p is the numerator and q is the denominator. A numerator is the part of a fraction above the fraction bar and represents the number of parts out of the whole, whereas a denominator is the total number of the parts. 

For example, in the fraction $\frac{4}{5}$, the numerator is 4, and the denominator is 5.

There are two types of fractions based on the denominator. 

• Like Fractions

The fractions with the same denominator are known as the like fractions. For example: $\frac{2}{7}$ and $\frac{5}{7}.$

• Unlike Fractions

The fractions with different denominators are known as unlike fractions. For example: $\frac{5}{7}$ and $\frac{4}{9}$

Definition of Unlike Denominators

We just learnt about fractions, their representation and types based on the value of the denominator. So, what are unlike denominators? 

When two or more fractions have different denominators, then the denominators of the fractions are known as, unlike denominators. 

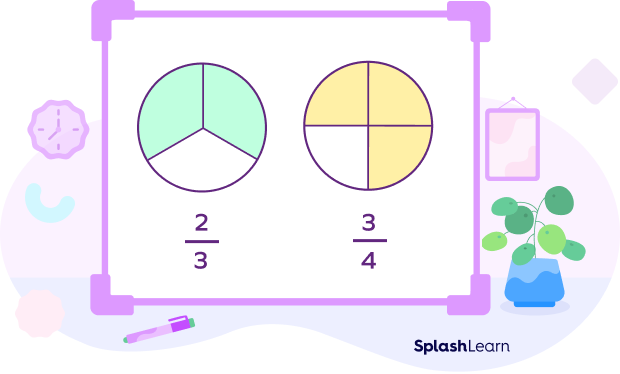
In the figure above, both fractions have different or unlike denominators.

It is challenging to compare and perform operations like addition and subtraction of fractions with unlike denominators. Hence, to compare and order, or to add and subtract unlike fractions, we first convert these fractions to like fractions, i.e., fractions with the same denominators.

How to Convert Unlike Denominators to Like Denominators?

When two or more fractions have different denominators, we can convert them into like fractions by finding the common denominator. Let’s explore more by considering the following example. 

Take the fractions $\frac{3}{4}$ and $\frac{5}{7}$. Both fractions have different denominators. To find their common denominators, we find the common multiples of the denominators 4 and 7.

Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, . . .

Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, . . .

The least common multiple of 4 and 7 is 28.

If we want the fractions to have a common denominator 28, we must find the equivalent fraction of $\frac{3}{4}$ and $\frac{5}{7}$, which has 28 as the denominator. 

So, now that we know what like and unlike denominators are, how do we apply them in fraction problems? We can easily compare, add or subtract two or more fractions when their denominators are common or like. Let’s now figure out how we can do this.

How to Compare Fractions with Unlike Denominators?

When the fractions have like or the same numerators but different denominators, like $\frac{3}{4}$ and $\frac{3}{7}$. We can now compare $\frac{3}{4}$ and $\frac{3}{7}$ by comparing the size of each piece. Since fourths are larger than sevenths, $\frac{3}{4}$ is greater than $\frac{3}{7}$ . 

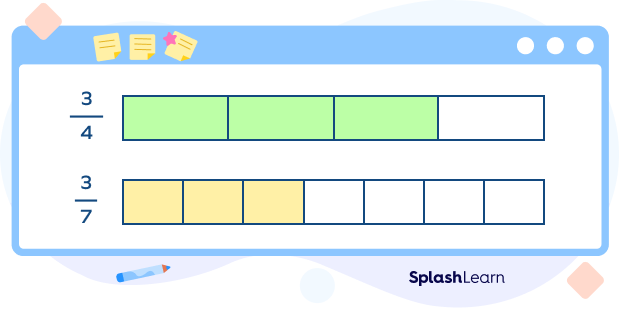
To compare two or more unlike fractions with the same or like numerators, we have to compare their denominators. The fraction with the smallest denominator is the greatest.

When the fractions are unlike with different numerators, we have to find the common denominator before we can compare. For example, let us compare $\frac{5}{6}$ and $\frac{2}{3}$.

Look at the two denominators (6 and 3). It is much easier to find a common denominator (6) than to find a common numerator. So, find a fraction equivalent to $\frac{2}{3}$ with 6 as a denominator $(\frac{2}{3} \times \frac{2}{2} = \frac{4}{6} )$. 

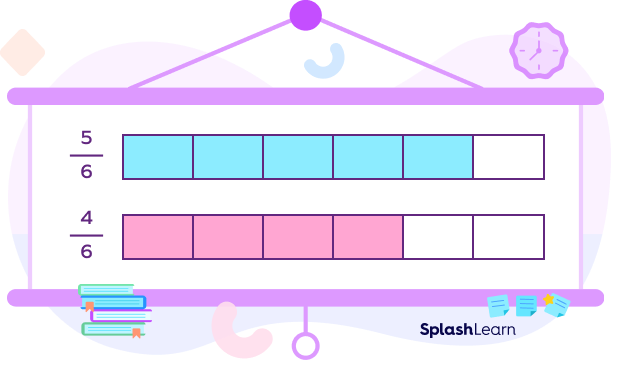
To compare two or more like fractions (with the same or like denominators), we have to compare their numerators. The fraction with the smallest numerator is the smallest.

When we compare fractions $\frac{4}{11}$ and $\frac{7}{11}$, we take a look at the numerators. Since 7 is more than 4,  $\frac{4}{11}\lt\frac{7}{17}$.

How to Add and Subtract Fractions with Unlike Denominators?

Adding and subtracting fractions with unlike denominators can be done by converting them to like fractions. Let’s understand more with an example: $\frac{1}{4} + \frac{2}{3}$. Here, we are adding fractions with unlike denominators 4 and 3. To add them, we can find the common denominator. Since the LCM of 4 and 3 is 12, the common denominator is 12. 

$\frac{1}{4} + \frac{2}{3} = \frac{1 \times 3}{4 \times 3} + \frac{2 \times 4}{3 \times 4} = \frac{3}{12} + \frac{8}{12} = \frac{11}{12}$ 

Similarly, to subtract two unlike fractions, we can convert them to like fractions and subtract the numerators. For instance, let’s subtract 19 from 27. Convert these to like fractions by finding the common denominator. Since the LCM of 7 and 9 is 63, the common denominator is 63. 

$\frac{2}{7} – \frac{1}{9} = \frac{2 \times 9}{7 \times 9} — \frac{1 \times 7}{9 \times 7} = \frac{18}{63}-\frac{7}{63} = \frac{11}{63}$ 

Solved Examples

1. Arrange $\frac{5}{11},\frac{5}{7},\frac{5}{17}$ and $\frac{5}{13}$ in the descending order. 

Solution:

The given fractions have different denominators but have the same numerators. In such a case, the fraction with the highest denominator is the smallest.

Since $7 \lt 11 \lt 13 \lt 17$,  $\frac{5}{7}\gt\frac{5}{11}\gt\frac{5}{13}\gt\frac{5}{17}$

2. Candy read $\frac{4}{7}$ of the book on Monday and $\frac{2}{3}$ of the book on Tuesday. On which day did she read more and by how much?

Solution: 

Fraction of book read on Monday $= \frac{4}{7}$

Fraction of book read on Tuesday $= \frac{2}{3}$

Since the fractions are unlike, we can convert them to like fractions to compare. To convert, let’s find the common denominator, which is the LCM of 7 and 3. 

LCM of 7 and 3 is 21, 

$\frac{4\times3}{7\times3}=\frac{12}{21}$ and $\frac{2\times7}{3\times7}=\frac{14}{21}$

Since the numerator 12 is less than 14, $\frac{12}{21} \lt \frac{14}{21}$.

So, $\frac{4}{7} \lt \frac{2}{3}$, and she read more on Tuesday. 

Difference $= \frac{14}{21}-\frac{12}{21}=\frac{14-12}{21}=\frac{2}{21}$

3. Add: $\frac{2}{3}+\frac{2}{5}+\frac{3}{4}$. 

Solution: 

LCM (3, 5 and 4) = 60

$\frac{2 \times 20}{3 \times 20}=\frac{40}{60};\frac{2 \times 12}{5 \times 12}=\frac{24}{60};\frac{3 \times 15}{4 \times 15}=\frac{45}{60}$

$\frac{2}{3}+\frac{2}{5}+\frac{3}{4} = \frac{40}{60}+\frac{24}{60}+\frac{45}{60}=\frac{109}{60}=1\frac{49}{60}$

4. Does the fraction of the shaded part in the following figures have like or unlike denominators?

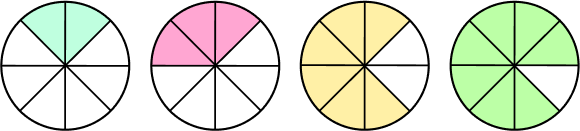
Solution: 

The fraction of the shaded parts in the given figure are $\frac{2}{8}, \frac{3}{8}, \frac{6}{8}, \frac{7}{8}$.

The denominators of the fractions are the same, i.e., 8, so the fractions have like denominators.

Practice Problems

Frequently Asked Questions