What Are Composite Numbers?
In math, composite numbers can be defined as numbers that have more than two factors. Numbers that are not prime are composite numbers because they are divisible by more than two numbers.
Examples:
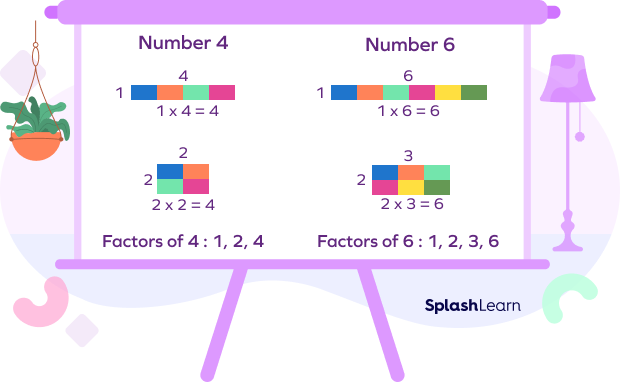
- Factors of 4 = 1, 2, 4 i.e.
Since 4 has more than two factors. So, 4 is a composite number.
- Factors of 6 = 1, 2, 3, 6
Since 6 also has more than two factors. So, 6 is also a composite number.
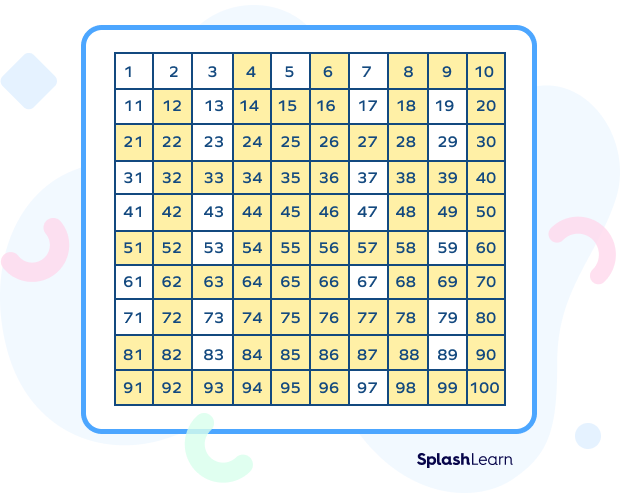
Following is the list of composite numbers from 1 to 100:
Fun Facts
- The numbers 0 and 1 are neither prime nor composite numbers.
- All even numbers except 2 are composite numbers.
- 4 is the smallest composite number.
- Each composite number can be written as a product of two or more primes.
- Composite numbers are divisible by other composite numbers.
- All composite numbers are always divisible by 1 and the number itself.
Recommended Games
Finding Composite Numbers
The divisibility test is a standard method used to find a composite number. In this test, the given number is divided by a smaller prime or composite number. If it is entirely divisible, the number is a composite number.
For example, 48 = $2 \times 2 \times 2 \times 2 \times 3$
Since 48 is divisible by 2 and 3, hence it is a composite number.
Recommended Worksheets
Types of Composite Numbers
There are two types of composite numbers:
- Odd composite numbers
- Even composite numbers
Odd Composite Numbers
Composite numbers with an odd digit in the unit’s place are odd composite numbers. In simple words, all the odd numbers that are not prime numbers are odd composite numbers.
For example: 9, 15, 21, etc.
Even Composite Numbers
Composite numbers with an even digit in the unit’s place are even composite numbers. In simple words, all the even numbers except 2 are even composite numbers. This is because no even number (except 2) can ever be a prime number.
For example: 8, 12, 14, etc.
Conclusion
A composite number is a positive integer divisible by smaller positive integers other than 1 and itself. Composite numbers can be identified by using the divisibility method.
Solved Examples on Composite Numbers
1. Check if 104 is a composite number or not.
The given number 104 is divisible by 2 and hence have more than 2 factors.
Therefore, it is a composite number.
2. Check if 111 is a composite number.
The given number is divisible by 3 and hence have more than 2 factors.
Therefore, it is a composite number.
3. Check if 179 and 144 are composite numbers.
Among the given numbers, 179 is not divisible by any number other than 1 and 179; therefore, it is not a composite number. 144 is divisible by 2, so it is a composite number.
Practice Problems on Composite Numbers
Composite number
Which is the smallest composite number among the following?
9 is the smallest composite number. It has more than two factors: 1, 3, and 9.
Which one of the following is not a composite number?
23 is not a composite number. It is only divisible 1 and itself.
Which of the following is a composite number?
20 is a composite number. It is divisible by more than two factors: 1, 2, 4, 5, 10, and 20.
What is the largest composite number among the following?
39 is the largest composite number among all the options with 1, 3, 13, and 39 as its factors. 47 is a prime number.
Frequently Asked Questions on Composite Numbers
Can a number be both prime and composite?
No, a number cannot be both prime and composite. A prime number has exactly two factors, 1 and itself, while a composite number has more than two factors. So, all natural numbers (except 1) are either prime or composite, but not both.
Is 0 a composite number?
Any number multiplied by zero gives the product 0. Hence 0 has an infinite number of factors. To be composite, a number must have more than two factors but not an infinite number of them. Hence, 0 does not qualify as a composite number.
What is the smallest composite number?
4 is the smallest composite number.
Are all even numbers composite numbers?
No. All even numbers except 2 are composite numbers. 2 has only two factors: 1 and 2.




































