What Are Odd Numbers?
A number which is not divisible by “2” is called an odd number. An odd number always ends in 1, 3, 5, 7, or 9.
Examples of odd numbers: $51,\;-\; 543, 8765,\;-\; 97, 9$, etc.
An odd number is always 1 more than (or 1 less than) an even number. For example, let us take an even number, 8. The odd number next to it is $8 + 1 = 9$. The odd number before it is $8 \;-\; 1 = 7$.
This explains that when you have an odd number of objects with you, you cannot divide them into equal groups!

Odd numbers are numbers which when divided by 2 leave the remainder 1.
In other words, we can say a number, which is not divisible by 2, is an odd number.
Examples: 1, 23, 535, 67, 12763489
Definition of Odd Numbers
Odd number can be defined as an integer that is not divisible by “2.”
These are the numbers that have 1, 3, 5, 7, or 9 at their ones place. Odd numbers are simply the integers that are not multiples of 2.
Recommended Games
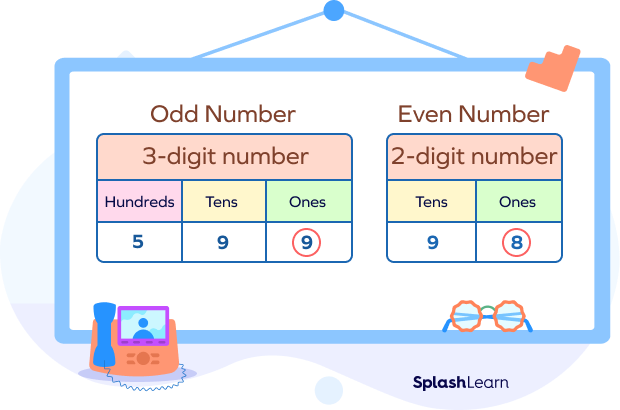
How to Identify Odd Numbers?
Let’s see how we identify odd numbers. Always look at the ones digit. If it is 1, 3, 5, 7, or 9, the number is odd. Otherwise, it is an even number.
Recommended Worksheets
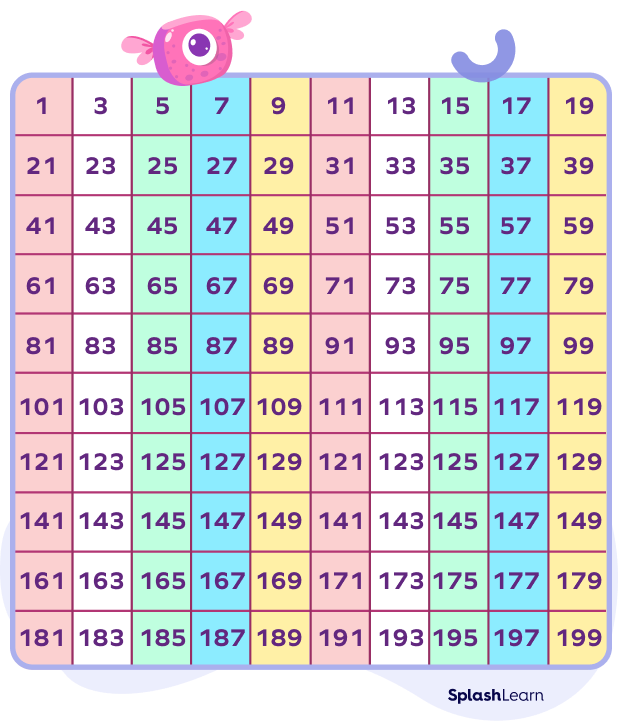
List of Odd Numbers $(1\;–\;200)$
The list of odd numbers from 1 to 200 is shown below. These are odd positive integers!
Types of Odd Numbers
There are two types of odd numbers given below:
Composite odd numbers:
The positive integers that have a factor other than 1 and itself are known as composite numbers. The numbers that are composite in nature but are not divisible by 2 are known as composite odd numbers. Example: 9, 15, 21
Consecutive odd numbers:
If x is an odd number, then the numbers x and $\text{x} + 2$ are consecutive odd numbers. These numbers follow each other in sequential order with a difference of two between them.
Properties of Odd Numbers
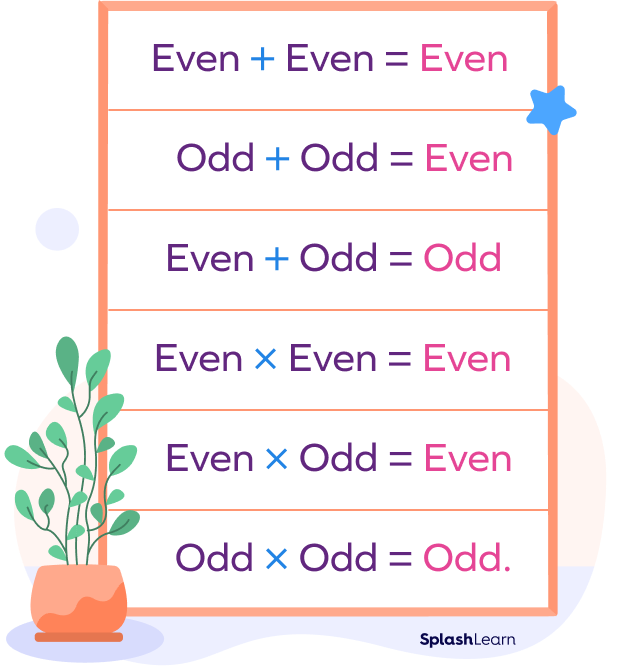
Properties of Addition
- Even number $+$ Odd number $=$ Odd number.
For example, $7 + 2 = 9$.
Even plus odd equals odd!
- Odd number $+$ Odd number $=$ Even number.
For example, $5 + 9 = 14$
Odd plus odd equals even!
- Even number $+$ Even number $=$ Even number
For example, $6 + 4 = 10$
Even plus even equals even!
Properties of Subtraction
- Even number $-$ Odd number $=$ Odd number
For example, $10 \;-\; 5 = 5$.
- Odd number $-$ Odd number $=$ Even number
For example, $11 \;-\; 3 = 8$.
Properties of Multiplication
- Multiplying an even number and an odd number (and vice- versa) always results in an even number.
For example, $7 \times 4 = 28$.
- Multiplying an even number with an even number always results in an even number.
For example, $2 \times 4 = 8$.
- Multiplying an odd number with an odd number always results in an odd number.
For example, $7 \times 3 = 21$.
- When we divide two odd numbers where the denominator is a factor of the numerator, the result is always an odd number.
Example: When we divide 9 by 3 where 3 is a factor of 9, we get 3, which is an odd number.
When we divide two odd numbers and the denominator is not a factor of the numerator then the result is a decimal number.
Let’s Summarize!
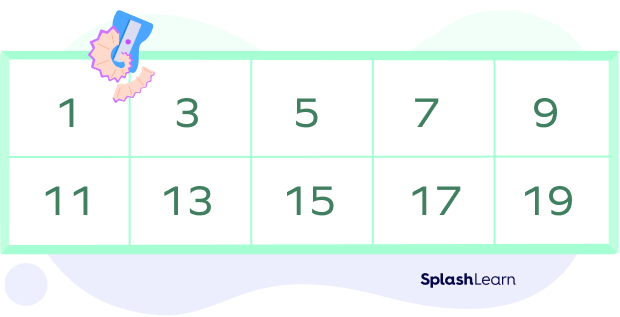
Odd Numbers Between 1 to 20
Odd numbers between 1 to 20 which are the first ten odd numbers are as follows.
What is the Smallest Odd Composite Number?
The smallest odd composite number is 9.
Check the list of odd numbers: 1, 3, 5, 7, 9, 11, …
Among these, 1 is neither prime nor composite. The numbers 3, 5, and 7 are not composite numbers. That makes 9 the smallest composite number.
Numbers that have factors other than 1 and itself are composite numbers. For example, 15.
15 is divisible by 1, 3, 6 and 15.
General Form of Odd Numbers
The general form of odd numbers is given by $2\text{k} + 1$, where $\text{k} \in \text{Z}$ (set of integers).
Fun Facts of Odd Numbers!
- When you add all the odd numbers from 1 to any number, the sum that you get will always be a perfect square.
- Example: The sum of odd numbers from 1 to 10 is 25, which is a perfect square.
- 0 is an even number.
- The first positive odd number is 1.
- Odd numbers are sometimes referred to as “uneven numbers” (meaning “not even”). However, the term ‘odd numbers’ is commonly preferred.
Let’s Sing!
One, three, five, seven and nine,
All standing in a straight line.
Divide them into equal teams,
One is left, and alone it seems!
Let’s Do This!
This is a fun activity. Put an odd number of beads in a box. Ask your child to count and determine if the total number of beads is even or odd. Next, give your child two empty boxes. Instruct them to divide the beads into the two boxes, such that each of them have an equal number of beads. Ask how many are left. Further, ask your child to pick out an even number of beads and then an odd number of beads. Show that the sum or difference of an even and odd number is odd.
Conclusion
In this article we learned about odd numbers. We discussed a few odd numbers and saw a chart of odd numbers. We also learned their properties and rules. There are various multiplicity rules and properties of odd numbers, which solve various mathematical problems.
Solved Examples of Odd Numbers
1. Identify odd numbers from the given list.
23, 46, 81, 73, 11, 8, 62
Solution:
Odd numbers are 23, 81, 73, 11 because they are not divisible by 2.
2. Find the sum of odd numbers between 50 and 60.
Solution:
The odd numbers that lies between 50 and 60 are
51, 53, 55, 57, 59
Sum of these numbers $= 51 + 53 + 55 + 57 + 59 = 275$
3. Check whether the sum of two odd numbers is odd or even.
Solution:
We know that an odd number is always 1 more than an even number. Let $2\text{x}$ and 2y be an even number.
So, $2\text{x} + 1$ and $2\text{y} + 1$ be the odd numbers
The sum of the numbers
$= (2x + 1) + (2 y+ 1)$
$= 2 x + 2 y + 2$
$= 2(x + y + 1)$
Let $\text{X} = x + y + 1$
Therefore, $(2 x + 1) + (2 y+ 1) = 2\text{X} =$ Multiple of $2 =$ Even number
4. What is the sum of the smallest and the largest 3-digit odd numbers?
Solution:
The smallest 3-digit odd number $= 101$
The largest 3-digit odd number $= 999$
Sum of the numbers $= 101 + 999 = 1100$
5. The lengths of the sides of a triangle are consecutive odd numbers. Then find out what the length of the longest side is if the perimeter of the triangle is 56 units?
Solution:
Let y be a positive odd number, so the odd number next to y is, $y + 2$ and $y + 4$.
So, $y, y + 2, y + 4$ are the lengths of the triangle.
Since we know that the perimeter of triangle $=$ sum of all the sides
$\Rightarrow 56 = y + y + 2 + y + 4$
$\Rightarrow 56 = 3y + 6$
$\Rightarrow y = \frac{50}{6}$
$\Rightarrow y = 16.66$
Practice Problems of Odd Numbers
Odd Numbers – Definition with Examples
Find the three consecutive odd integer numbers whose sum is 123?
Let $x,\; x + 2,\; x + 4$ are the three consecutive odd integers.
$\Rightarrow x + x + 2 + x + 4 = 123$
$\Rightarrow 3x + 6 = 123$
$\Rightarrow 3x = 117$
$\Rightarrow x = 39$
Now, the rest of the numbers are $x + 2$ and $x + 4$. So, $39 + 2 = 41$ and $39 + 4 = 43$.
Hence, the three numbers are 39, 41 and 43.
0 is an____ number.
0 is an even number.
What is the smallest positive odd number?
The smallest positive odd number is 1.
Find the number from below which is not an odd number ?
70 is not an odd number since it ends with “0.”
Find the group which has only odd numbers ?
The last group lists only odd numbers.
Frequently Asked Questions of Odd Numbers
What is divisibility?
The capacity of a number to be evenly divided by any number, without leaving a remainder is said to be “divisible” and this property is called divisibility.
Is 1 an odd number?
Yes, 1 is an odd number because it is not divisible by 2.
Find the odd number that comes after 999?
The odd number after 999 is 1001.
What is the general form of an odd number?
Yes, to express an odd number we use a formula that is expressed as $2n \pm 1$, where, n $\in$ W.
Can odd numbers be negative?
Yes, integers that are not multiples of 2 are odd numbers. Thus, odd numbers can be positive or negative.




































