Divisible
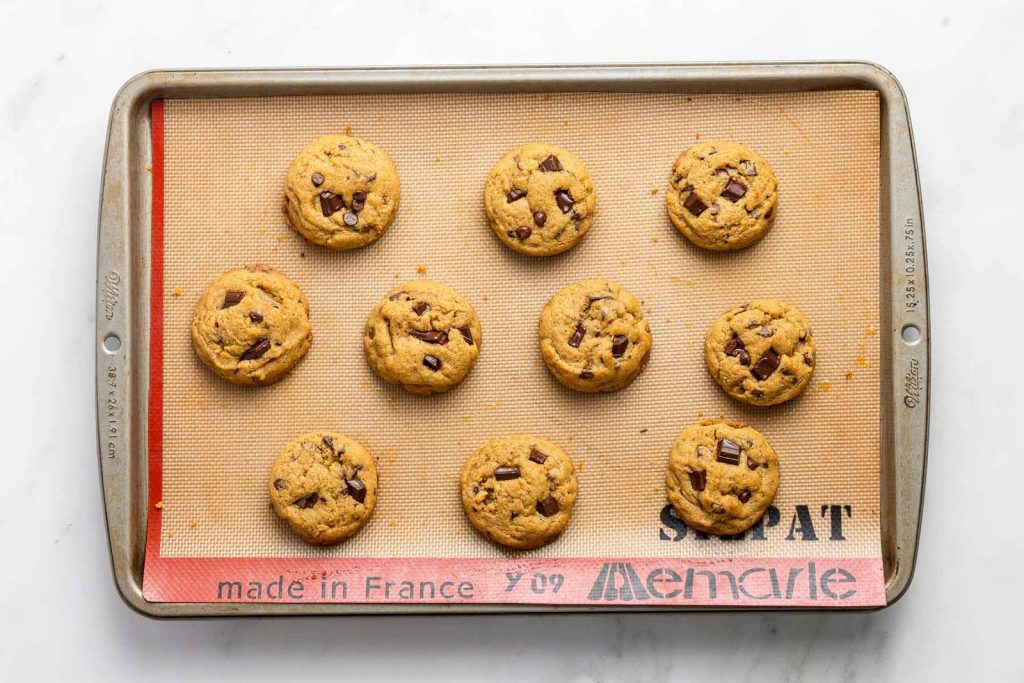
Imagine 3 friends trying to share 10 cookies. Each of them gets 3 cookies, and there’s one cookie leftover. They are unsure about what to do with it; would one person get an extra cookie? That did not seem fair to the 3 friends, who loved sharing everything equally.
If there were 9 cookies, they would have divided the cookies amongst themselves equally, and there would have been no confusion. Because 9 is divisible by 3. This means that 9 cookies could have been divided into three equal parts without there being any extra cookies left.
Recommended Games
What Does Divisible Mean?
In math, a number is said to be exactly divisible by another number if the remainder after division is 0.
Recommended Worksheets
Divisibility Rules
Divisibility rules are a set of general rules that are often used to determine whether or not a number is absolutely divisible by another number. Divisibility rules can help you employ a quick check to determine whether a number will be totally divisible by another number.
Let’s look at some divisibility rules:
Divisibility Rule of 1
Every number ever is divisible by 1. Think of any number, no matter how big or small, like 423 or 45678, they are all divisible by 1.
Divisibility Rule of 2
Every even number is divisible by 2. That is, any number that ends with 2, 4, 6, 8, or 0 will give 0 as the remainder when divided by 2. For example, 12, 46, and 780 are all divisible by 2.
Divisibility Rule of 3
If the sum of the digits of a number is divisible by 3, then the number as a whole would also be divisible by 3. For example, take the number 753.
$7 + 5 + 3 =$ 15. 15 is divisible by 3, and so, 753 is also divisible by 3.
Divisibility Rule of 4
If the number formed by just the last two digits of a number is divisible by 4, then the number as a whole is also divisible by 4. For example, take the number 3224. The last two digits are 24, which forms a number that is divisible by 4. So, 3224 is also divisible by 4.
Divisibility Rule of 5
If a number ends with 0 or 5, it is divisible by 5. For example, 35, 790, and 55 are all divisible by 5.
Divisibility Rule of 6
If a number is divisible by 2 and 3 both, it will be divisible by 6 as well. For example, 12 is divisible by both 2 and 3, and so it is divisible by 6 as well.
Divisibility Rule of 7
This one is a little tricky to understand. If the difference between the double of the last digit and the remaining digits of a number is divisible by 7, the number as a whole will be divisible by 7. Did you understand that? Let’s try it with an example: take the number 343. The last digit is 3. The double of 3 is 6. Now, if we were to get the difference of the remaining digits with 6, it would be $34 – 6 = 28$, which is divisible by 7. Hence, 343 is also divisible by 7.
Divisibility Rule of 8
This one also needs a little practice to understand. If the number formed by the last three digits of a number is divisible by 8, we say that the original number is divisible by 8. For example, in the number 4176, the last 3 digits are 176. If we divide 176 by 8, we get:
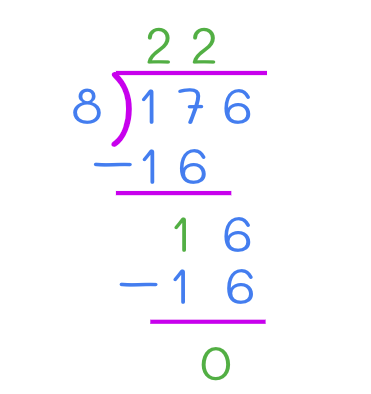
Since 176 is divisible by 8, 4176 is also divisible by 8.
Divisibility Rule of 9
Just like the divisibility rule of 3, if the sum of the digits of a number is divisible by 9, then the number as a whole will also be divisible by 9. For example, take the number 882.
$8 + 8 + 2 =$ 18. 18 is divisible by 9, and so, 882 is also divisible by 9.
Divisibility Rule of 10
If the last digit of a number is 0, it is always divisible by 10. For example, 200, 30, and 67890 are all divisible by 10.
Divisibility Rule of 11
This is perhaps the most interesting of all the divisibility rules. In a given number, if the difference between the sums of the odd digits and even digits of the number is 0 or is a number divisible by 11, then it is divisible by 11.
Fun Fact!
| When a number is divisible by another number, it is also divisible by each of the factors of that number. For instance, a number divisible by 6 will also be divisible by 2 and 3. A number divisible by 10 is also divisible by 5 and 2. |
Solved Examples on Divisible
Example 1: If a number is divisible by 4, can we say it is divisible by 2 as well?
Solution: Yes, because 4 is divisible by 2.
Example 2: The sum of the digits of a number is divisible by 9. The last two digits of the number are divisible by 4. Is the whole number divisible by 12?
Solution: Yes, if the number is divisible by 9, we can conclude that it is divisible by 3 as well (as 3 is a factor of 9).
Since it is divisible by 3 and 4, it is divisible by 12 (once again, the rule of factors applies).
Example 3: The sum of the digits of a round number is divisible by 3. Is the number divisible by 6?
Solution: Yes. If the sum of the digits is divisible by 3, the number is divisible by 3.
Since it is a round number, i.e., it ends in 0, it is an even number and is divisible by 2.
Since it is divisible by both 3 and 2, it is divisible by 6.
Practice Problems on Divisible
Divisible - Definition with Examples
Which of the following numbers is divisible by 7?
Since the last digit is 1, the double of 1 is 2, and $37 – 2 = 35$. Since 35 is divisible by 7, therefore 371 is divisible by 7.
We know that 165 is divisible by 3. Which of the following numbers is 165 also divisible by?
The sum of the odd digits in 165 is $1 + 5 = 6$
The sum of the even digits in 165 is 6
The difference is $6 – 6 = 0$
Therefore, 165 is divisible by 11.
An even number is divisible by 3. Which of the following numbers is it also divisible by?
Since it is an even number, it must be divisible by 2. Since it is divisible by both 3 and 2, it is also divisible by 6.
Frequently Asked Questions on Divisible
If a number is only divisible by 1 and itself, what is it called?
If a number is only divisible by 1 and itself, it is called a prime number.
What is a composite number?
A composite number is a number that is divisible by numbers other than 1 and itself.
When is a number said to be a factor of another number?
A number x is said to be a factor of number y if y is divisible by x. For example, 10 is divisible by 2, so 2 is a factor of 10.




































