What Are Even and Odd Numbers?
Even and odd numbers are fundamental in elementary math. They naturally boost kids’ understanding of other math concepts such as the divisibility rule of 2, division with or without remainders, or equal sharing!
What is an even number? An even number can be easily divided into equal groups. How? Let’s see!
Can you count the number of kids in the given picture and tell me if you can divide them equally among 2 teams?

There are 4 kids. They can be easily divided into two equal teams since 4 is an even number.

Let’s take another example. Assume you have 10 chocolates. These chocolates can be divided into two groups, each having five chocolates. So, 10 is an even number.
However, 11 chocolates cannot be grouped in this way, so 11 is not an even number. An odd number is a number that is not divisible by 2. The remainder in the case of an odd number is always “1”. 11 is an odd number.
Recommended Games
Even Number Definition
A number that is divisible by 2 and generates a remainder of 0 is called an even number. Even numbers are evenly divisible by 2. When divided by 2, even numbers leave a remainder of 0. Even numbers always end with 0, 2, 4, 6, or 8.

Even numbers examples: 22, 56, 98, 2, -16, 452, -867454, 12, 5752452, -98534, etc.
Recommended Worksheets
Odd Number Definition
Odd numbers are numbers that are not evenly divisible by 2. When divided by 2, even numbers leave a remainder of 1. They always end with 1, 3, 5, 7, or 9.
Odd numbers examples: 25, 51, 99, 21, -17, 477, -867453, 13, 572789, -983455, etc.
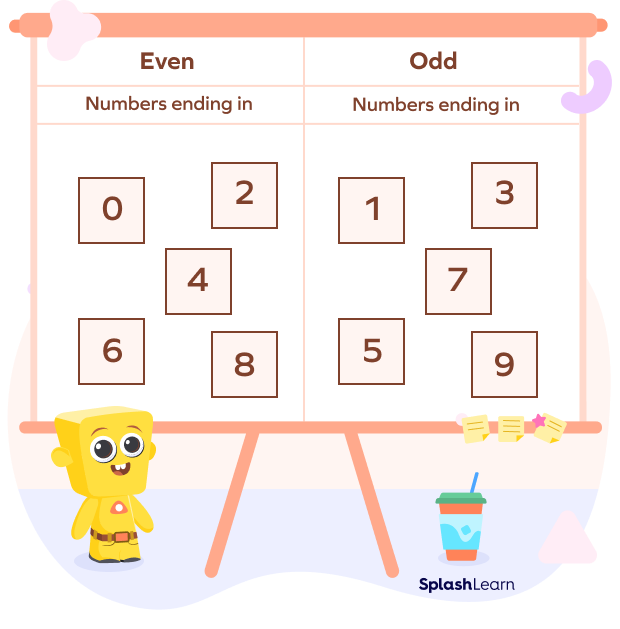
In the sections below, we’ll examine some additional intriguing methods for grasping even numbers, their features, and fun facts about them.
How Do We Identify Even and Odd Numbers?
1. By comprehending the number at the “ones” place
In this approach, we analyze the number in the “ones” place in an integer to check if the number is even or odd. All the numbers ending with 0, 2, 4, 6 and 8 are even numbers. For example, numbers such as 14, 26, 32, 40 and 88 are even numbers.
To identify even numbers, we observe the last digit or the ones digit of the number. If it ends in the digits 0, 2, 4, 6, or 8, then it is an even number. Otherwise, it is an odd number.
Example 1: 248
| Hundreds | Tens | Ones |
|---|---|---|
| 2 | 4 | 8 |
| Even Number | ||
Example 2: 103
| Hundreds | Tens | Ones |
|---|---|---|
| 1 | 0 | 3 |
| Odd Number | ||
2. By grouping
If we divide a number into two groups with an equal number of elements in each, then the number is an even number. Simply divide the number by 2. If the remainder is “0,” then it is an even number; if the remainder is 1, then it is an odd number.
Example 1: $\frac{72}{2} = 36$ and remainder = 0
Thus, 72 is an even number.
Example 2: $\frac{35}{2} = 17$ R 1 since $(17 \times 2) + 1 = 35$
Thus, 35 is an odd number.
Even and Odd Numbers on a Number Line
On a number line, if you start from 0 and keep taking jumps of 2, you will land on 2, 4, 6, 8, 10, and so on. These are even numbers.
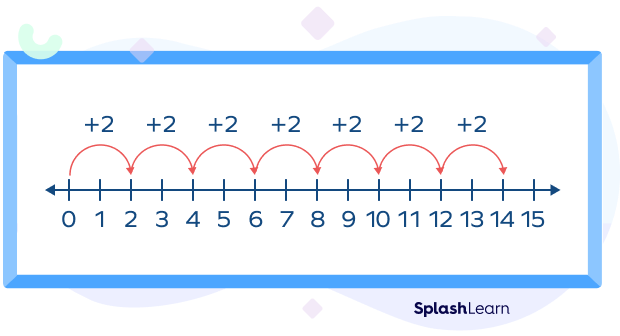
If you make the jumps of 2 to the left of 0, you will meet the negative integers that are even. Notice that between two even numbers, there’s an odd number!

General Form of Even and Odd Numbers
Let n be any integer, then even numbers can be expressed as 2n.
General form of even numbers = 2n n is an integer
General form of odd numbers = 2n + 1 or 2n – 1 n is an integer
For example, if n = 3, we get an even number 6 and an odd number 7.
For n = – 5, we get an even number – 10 and an odd number – 9.
Properties of Even and Odd Numbers
Take a look at the properties of even and odd numbers, such as addition, multiplication, and subtraction.
Property of Addition
- Even number + Odd number = Odd number
An even number plus an odd number equals an odd number.
For example, 8 + 5 = 13; 6 + 7 = 13
- Even number + Even number = Even number
Adding two even numbers results in an even number.
For example, 8 + 4 = 12; 12 + 8 = 20
- Odd number + Odd number = Even number
When adding two odd numbers, the result is an even number.
For example, 3 + 5 = 8; 15 + 11 = 26

Property of Subtraction
- Even number – Odd number = Odd number
When you subtract an odd number from an even number, the result is an odd number.
For example, 8 – 5 = 3; 32 – 6 = 26
- Even number – Even number = Even number
Subtracting two even numbers results in an even number.
For example, 16 – 10 = 6; 37 – 4 = 33
- Odd number – Odd number = Even number
Subtracting two odd numbers results in an even number.
For example, 13 – 5 = 8; 63 – 17 = 46

We can summarize the addition and subtraction properties as follows:
| Addition | Subtraction | Result |
|---|---|---|
| Even + Even | Even – Even | Even |
| Even + Odd | Even – Odd | Odd |
| Odd + Even | Odd – Even | Odd |
| Odd + Odd | Odd – Odd | Even |
Property of Multiplication
- Multiplying an even number and an odd number (and vice versa) always results in an even number.
For example, 5 × 6 = 30.
- Multiplying an even number with an even number always results in an even number.
For example, 6 × 10 = 60.
- Multiplying odd and odd always results in an odd number.
For example, 13 × 5 = 65.
| Operation(×) | Result |
|---|---|
| Even × Even | Even |
| Even × Odd | Even |
| Odd × Even | Even |
| Odd × Odd | Odd |
Here are some examples:

List of Even and Odd Numbers up to 100
| Even Numbers up to 100 | ||||
|---|---|---|---|---|
| 2 | 4 | 6 | 8 | 10 |
| 12 | 14 | 16 | 18 | 20 |
| 22 | 24 | 26 | 28 | 30 |
| 32 | 34 | 36 | 38 | 40 |
| 42 | 44 | 46 | 48 | 50 |
| 52 | 54 | 56 | 58 | 60 |
| 62 | 64 | 66 | 68 | 70 |
| 72 | 74 | 76 | 78 | 80 |
| 82 | 84 | 86 | 88 | 90 |
| 92 | 94 | 96 | 98 | |
| Odd Numbers up to 100 | ||||
|---|---|---|---|---|
| 1 | 3 | 5 | 7 | 9 |
| 11 | 13 | 15 | 17 | 19 |
| 21 | 23 | 25 | 27 | 29 |
| 31 | 33 | 35 | 37 | 39 |
| 41 | 43 | 45 | 47 | 49 |
| 51 | 53 | 55 | 57 | 59 |
| 61 | 63 | 65 | 67 | 69 |
| 71 | 73 | 75 | 77 | 79 |
| 81 | 83 | 85 | 87 | 89 |
| 91 | 93 | 95 | 97 | 99 |
Facts about Even and Odd Numbers
- 0 is an even number.
- 1 is an odd number.
- The sum of two or more even numbers is always even.
- The product of two or more even numbers is always even.
- If you can form two equal groups of the given number, or form a “doubles fact,” it is an even number
Solved Examples on Even and Odd Numbers
Example 1: Is 29,510 an even number?
Solution:
The ones place of the given number is 0, which is an even number. Thus, the number 29,510 is an even number.
Example 2: What is the sum of the first and last even numbers between 1 and 100?
Solution:
Between 1 and 100, the largest even number is 98, and the smallest even number is 2.
So, the required sum is 98 + 2 = 100.
Example 3: What is the formula for the sum of the first n even number series?
Solution:
The formula of the sum of the first n even numbers is
1 + 2 + 3 + …+ n = n × (n + 1)
Example 4. Identify the even numbers from the given list.
23,8, 46, 81, -96, 73, -11, 62, 33, 74
Solution:
Even numbers are divisible by 2 and end in the digits “0”,”2″, “4”, “6” or “8”.
The even numbers here are 8 , 46,-96, 62 , 74.
Example 5. Find the sum of even numbers between 50 and 60.
Solution:
The even numbers that lie between 50 and 60 are as follows:
52, 54, 56,58
52 + 54 + 56 + 58 = 220
Sum = 220
Example 6. Check whether the number of apples in the image are even or odd.

Solution:
There are 11 apples.
11 apples cannot be divided into two equal groups. If we divide 11 by 2, the remainder is 1. One apple will be left out.
Thus, 11 is an odd number.
Example 7. What is the sum of the smallest and the largest three-digit even numbers?
Solution:
The smallest three-digit even number = 100
The largest three-digit even number = 998
Sum of the numbers = 100+ 998= 1098
Example 8. The lengths of the sides of a triangle are consecutive even numbers. Find out what the length of the longest side is if the perimeter of the triangle is 24 units?
Solution:
Let n be any positive number. Three consecutive even numbers can be represented as
2n, 2n+2, 2n+4
So, 2n, 2n+2,& 2n +4 be the lengths of the triangle.
Perimeter of triangle = Sum of all the sides
⇒ 24 = 2n + 2n + 2 + 2n + 4
⇒ 24 = 6n + 6
⇒ 6n = 18
⇒ n = 18 ÷ 6
⇒ n = 3
Hence, the lengths of the sides are
2n = 2 × 3 = 6
2n + 2 = 2 × 3 + 2 = 8
2n + 4 = 2 × 3 + 4 = 10
So, the length of the longest side is 10 units.
Practice Problems on Even and Odd Numbers
Even Numbers - Definition With Examples
Is 350 an even number?
350 is an even number because it is exactly divisible by 2.
Which of these are the examples of even numbers?
2, 16, 234 are the numbers divisible by 2.
How many even numbers are there between 20 and 50 (excluding 20 and 50)?
There are 16 even numbers between 20 and 50.
They are 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48.
What are the three consecutive even numbers whose sum is 72?
Let the three consecutive even numbers be $2n, 2n + 2$,and $2n + 4$.
Sum of the numbers $= 72$
$⇒ 72 = 2n + 2n + 2 + 2n + 4$
$⇒ 72 = 6n + 6$
$⇒ 6n = 66$
$⇒ n =11$
Hence, the numbers are
$2n = 2 × 11 = 22$
$2n + 2 = 2 × 11 + 2 = 24$
$2n + 4= 2 × 11 + 4 = 26$
The three consecutive even numbers are 22, 24, and 26.
Identify an even number.
100 is an even number since it ends with 0.
What is the smallest positive even number?
The smallest positive even number is “2.”
The number 0 is _______.
0 is an even number.
0 is not a positive number.
Frequently Asked Questions about Even and Odd Numbers
What is the prime number that is even?
The only number that is both prime and even is 2.
Which of the numbers among 11, 22, 81, and 5 is even?
In the given list, 22 is an even number since it is divisible by 2.
After dividing an even number by two, what is the remainder?
An even number is divisible by two precisely; hence, the remainder will be 0.
What is the difference between two even numbers?
When an even number is subtracted from another, the result is always an even number.
What is the divisibility rule of 2?
A number is divisible by 2 if it has 0, 2, 4, 6, or 8 at the ones place.
Is 1 an odd number?
Yes, 1 is an odd number because it is not divisible by 2.
Why is 0 called the whole number?
Can negative numbers be even?
Yes, negative numbers can be even. Even numbers can be both negative or positive.
Can even numbers be negative?
Yes, even numbers can be positive or negative. We refer to the negative even numbers as negative even integers.




































