Coprime Numbers: Definition, Steps, List, Properties, Examples

What Are Coprime Numbers?

Prime numbers have only two common factors—1 and the number itself. Likewise, coprime numbers are the numbers that have 1 as the only common factor. Additionally, we can state that a set of numbers is coprime if their highest common factor (HCF) is 1.

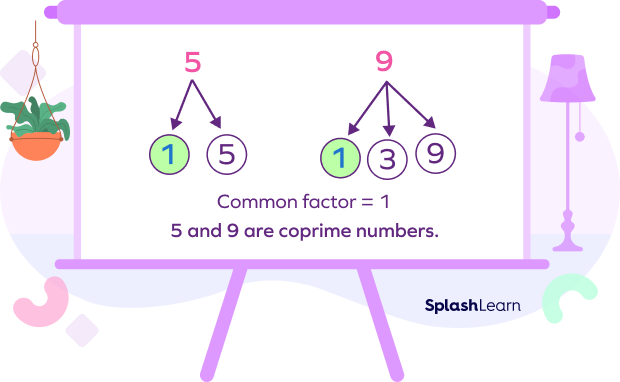
Example: Are 9 and 5 coprime?

Factors of 5: 1, 5 

Factors of 9: 1, 3, 9 

Common factor of 5 and 9: 1

Thus, 5 and 9 are coprime.

Coprime Numbers: Definition

When a pair of numbers have a common factor of 1, the two numbers are called coprime numbers. Coprime numbers are also known as “relatively prime numbers” or “mutually prime numbers.” 

Remember that two numbers do not have to be prime numbers to be coprime numbers. Coprime numbers can also be composite numbers (a number with more than two factors) if their common factor is 1.

Here are some examples of coprime numbers.

Example 1: 3 and 16

Factors of 3: 1, 3 

Factors of 16: 1, 2, 4, 8, 16 

Here, the only common factor between 3 and 16 is 1. 

HCF$(3, 16) = 1$. 

Thus, 3 and 16 are both coprime numbers.

Example 2: Are 6 and 9 coprime?

Factors of 6: 1, 3, 6 

Factors of 9: 1, 3, 9

Common factors: 1, 3

GCD $(6,9) = 3$

Thus, 6 and 9 are not coprime.

How to Find Coprime Numbers

According to the definition of coprime numbers, the provided set of numbers will be coprime if there is only one common factor between them, which is 1. 

To find whether two numbers are relatively prime or not, we find the Highest Common Factor (HCF) (or Greatest Common Divisor GCD) of the given numbers.

If the HCF is 1, then the two numbers are said to be relatively prime numbers.

To find the HCF of two numbers, we first list all the factors and then identify the highest common factor out of those.

Example: Check whether 4 and 5 are coprime.

Factors of 4: 1, 2, 4

Factors of 5: 1, 5

HCF $(4, 5) = 1$

Thus, 4 and 5 are coprime since their HCF is 1.

Steps to Find Coprime Numbers

Here are some easy steps that we can follow to determine whether the given set of numbers is coprime or not:

Step 1: List the factors of each number. 

Step 2: Identify all the common factors shared among the specified numbers.

Step 3: Next, find the factor with the greatest common denominator (or HCF). If it is 1, the specified numbers are coprime; otherwise, they are not.

Example 1: Are the numbers 9 and 14 coprime?

Factors of 9: 1, 3, 9

Factors of 14: 1, 2, 7, 14.

1 is the common factor shared between 9 and 14

Since the greatest common denominator (or HCF) is 1, 9, and 14 are coprime numbers. 

Example 2: Check if 15 and 14 are coprime.

Factors of 15: 1, 3, 5, 15 

Factors of 14: 1, 2, 7, 14

1 is the common factor shared between 15 and 14.

Since the greatest common denominator (or HCF) is 1, 15, and 14 are coprime numbers. 

Example 3: Are 11 and 19 coprime?

Factors of 11: 1, 11 

Factors of 19: 1, 19

1 is the common factor shared between 11 and 19.

Since the GCD is 1, the numbers 11 and 19 are coprime numbers. 

List of Coprime Numbers

Number	Coprime Number Pairs
1	(1, 3), (1, 4), (1, 5)  (1, 6), (1, 7), (1, 8), …, (1, 60), …
2	(2, 3), (2, 5), (2, 7), (2, 9), (2, 11), …, (2, 27), …
3	(3, 4), (3, 5), (3, 7), (3, 10), (3, 11), …, (3, 20), …
4	(4, 5), (4, 7), (4, 9), (4, 11), (4, 13), (4, 15), …
5	(5, 6), (5, 7), (5, 8), (5, 9), (5, 11), (5, 12), …
6	(6, 7), (6, 11), (6, 13), (6, 16), (6, 17), (6, 19), …

Properties of Coprime Numbers

•  If the GCF of any two numbers is 1, then the numbers are coprime numbers.

• Two consecutive numbers are always coprime numbers.

For example: (3, 4), (5, 6), (8, 9), (11, 12) (21, 22), (37, 38), (58, 59), (99, 100), …

• The number 1 is coprime with any other number.

For example: (1, 2), (1, 3), (1, 10), (1, 35), (1, 587), (1, 9999), …

• Since two even numbers always have two common factors, 1 and 2, they can never be coprime numbers.

For example: (2, 4), (6, 10), (12, 22), (16, 24), (80, 100). None of these combinations are coprime numbers.

• The sum and the product of two coprime numbers will always be coprime.

For example: $(6, 7);\; 6 + 7 = 13$ & $6 7 = 42$. Consequently, (13, 42) is a pair of coprime numbers.

• The product of two coprime numbers will always be their Least Common Multiple (LCM).

For example: (11, 13) Here, 11 and 13 are coprime numbers, and their LCM is $11\times13 = 143$.

• Because prime numbers only share one common factor, 1, any two prime numbers are always coprime. So, are all prime numbers coprime? Yes!  

For example: (11, 13), (17, 19)

Here, all of these pairs share only one factor, or 1. Therefore, each of these prime numbers is coprime.

Coprime Numbers from 1 to 100

From 1 to 100, you can find several coprime numbers that follow the properties mentioned above. These are as follows:

(13, 14)	(2, 9)	(28, 57)	(1, 99)	(13, 15)
(4, 97)	(39, 40)	(46, 67)	(75, 41)	(87, 89)
(99, 100)	(17, 19)	(13, 42)	(12, 35)	(9, 25)

In addition, any number paired with 1 forms a coprime pair, such as (1, 2), (1, 3), …, (1, 99), (1, 100). Thus, there are many coprime numbers from 1 to 100. 

Facts about Coprime Numbers

• It is not necessary that coprime numbers must be prime numbers. Two composite numbers can also be coprime. Example: (9, 25), (12, 35)
• Two even numbers are never coprime. 
• 1 is relatively prime with every number even itself.
• 0 and 1 are relatively prime numbers, as the common factor is 1.
• The Least Common Multiple (LCM) of two relatively prime numbers is always equal to their product.
• Any two prime numbers are always coprime.
• Any two consecutive numbers are coprime.

Conclusion

In this article, we have learned that coprime numbers are those whose HCF equals 1. Furthermore, it should be mentioned that coprime numbers need not be prime numbers. Let’s practice some examples to get a better understanding of coprime numbers. 

Solved Examples on Coprime Numbers

Example 1: Are 5 and 9 coprime numbers?

Solution:

To check whether 5 and 9 are coprime numbers, find the HCF (Highest Common Factor) of both numbers.

Factors of 5: 1, 5

Factors of 9: 1, 3, 9

Since the highest common multiple between 5 and 9 is number 1. Thus, these are coprime numbers. 

Example 2: Verify whether 350 and 148 are coprime numbers or not.

Solution:

Firstly, write down all the factors of 250 and 148. 

Factors of 148: 1, 2, 4, 37, 74, 148

Factors of 350: 1, 2, 5, 7, 10, 14, 25, 35, 50, 70, 175, 250

HCF $(148, 350) = 2$

350 and 148 are not coprime numbers.

Example 3: Are 40 and 78 coprime?

Solution: 

40 and 78 are both even numbers.

Since two even numbers always have two common factors, 1 and 2, they can never be coprime numbers.

Thus, 40 and 78 are not coprime numbers. 

Practice Problems on Coprime Numbers

Frequently Asked Questions on Coprime Numbers