Common Factor
Number sense plays a vital role in understanding numbers in math. At times, it is referred to as the number theory. It helps us study the meaning of numbers and their relationships. These skills are essential because they lay the foundation for more advanced skills. In this article, we will take a detailed look into one of the attributes of numbers, common factors. But before we delve into that, let’s understand more about “factors.”
Recommended Games
What Is a Factor?
Factors are numbers you can multiply together to get another number, called the product.
For example, consider the figure below.
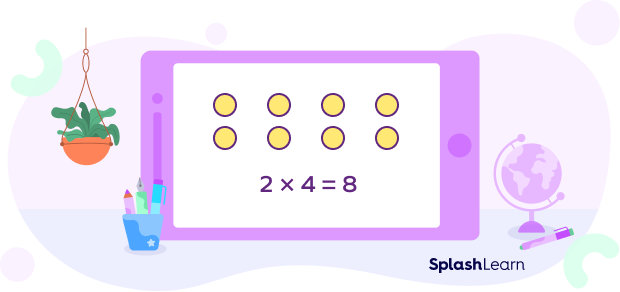
$2 \times 4 = 8,$ so 2 and 4 are both factors of 8.
If we divide a number by any one of its factors, there will be no remainder. In other words, a factor of a number evenly divides the number, leaving zero as the remainder.
A number can have two or many more factors. Let’s review this with an example: we can express the number 12 as shown in the figure below.
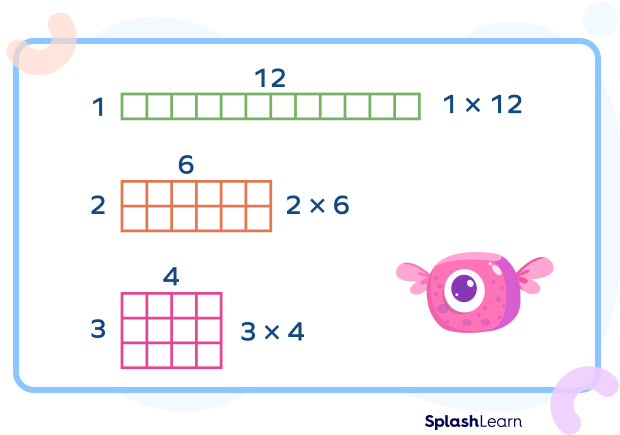
We can write 12 as the product of $1 \times 12, 2 \times 6,$ or $3 \times 4$.
Therefore 1, 2, 3, 4, 6, and 12 are all factors of 12. And if we divide 12 by 1, 2, 3, 4, 6, or 12, we get zero as the remainder. So, the number 12 is evenly divided or divisible by its factors.
Properties of Factors
- Every number is a factor of itself.
- 1 is a factor of every number.
- Each factor of a number is less than or equal to the number.
- The number of factors of a number is finite.
In mathematics, numbers sometimes have some features in common. When two or more numbers share a factor, we say they have a common factor. Let’s explore more!
Recommended Worksheets
What are Common Factors?
As the name implies, a common factor is a factor shared or joint between two or more numbers. In other words, it is a number that can evenly divide a set of two or more numbers.
Let’s discuss an example of common factors of 24 and 30.
Observe the factors of the numbers 24 and 30 on the number tiles below. A blue circle marks the factors of 24, and factors of 30 are in the pink circle.

The numbers with red and black circles give us the list of the common factors of 24 and 30.
Therefore, common factors of 24 and 30 are 1, 2, 3, and 6.
We can find the common factors of two or more numbers by listing the factors of each number and then identify the factors that are common among them.
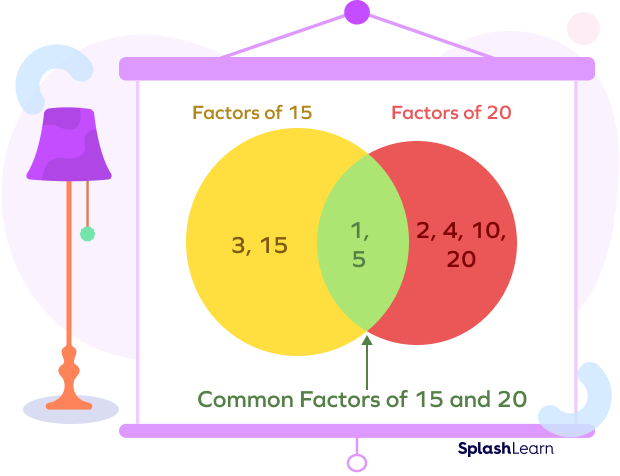
For example, let’s find the common factors of 15 and 20.
Factors of 15 are 1, 3, 5, and 15
Factors of 20 are 1, 2, 4, 5, 10 and 20
Observe the figure to identify the factors shared in 15 and 20.
Factors common in 15 and 20 are 1 and 5.
What is the Greatest Common Factor?
The greatest common factor (GCF) is the term used to describe the biggest number that can evenly divide a set of two or more numbers. It is also referred to as the greatest common divisor (GCD) or highest common factor (HCF).
To find the GCF of a set of numbers, we can list the factors of each number and identify the greatest factor common between them. Let’s take a quick example of finding the greatest common factor between 24 and 18.
Let’s start by listing out the factors.
Factors of 24: 1, 2, 3, 4, 6, 8, 12, and 24
Factors of 18: 1, 2, 3, 6, 9, and 18.
Common factors for both numbers would be 1, 2, 3, and 6. The greatest common factor here will thus be 6.
Applications of Common Factors
Common factors come in handy when simplifying fractions. A common factor between the numerator and denominators can reduce the fraction into the simplest form. Other applications of this topic include comparing prices and understanding time–work problems. Factorization and identifying GCF is a math skill we use every day. So, needless to say, it is an important skill!
Fun Facts
- The smallest common factor between any two even numbers is 2.
- If the only common factor of two numbers is 1, the numbers are called co-prime numbers.
- Consider two whole numbers A and B, such that A is less than B. Then the common factors of A and B are either less than or equal to A.
- Consider two whole numbers A and B, such that B is a multiple of A. Then the greatest common factor between A and B is A.
Solved Examples
1. Find the common factors of 19 and 15.
Solution: The factors of 19 and 15 are as follows:
Factors of 19 are 1, 19.
Factors of 15 are 1, 3, 5, 15.
The common factor for 19 and 15 is 1. Hence, they are co-prime numbers.
2. Find the factors common between 25 and 35.
Solution: The factors 25 and 35 are as follows:
Factors of $25 = 1, 5,$ and 25
Factors of $35 = 1, 5, 7$ and 35
Thus, the factors common between 25 and 35 are 1 and 5.
3. Find the greatest common factor of 9, 18, and 27.
Solution: The factors of 9, 18, and 27 are as follows:
Factors of $9 = 1, 3,$ and 9
Factors of $18 = 1, 2, 3, 6, 9,$ and 18
Factors of $27 = 1, 3, 9,$ and 27
The common factors of 9, 27, and 18 are 1, 3, and 9.
So, the greatest common factor of 9, 18, and 27 is 9.
Practice Problems
Common Factors
Which of the following is not a common factor of 12 and 24?
Since 24 is the multiple of 12, the common factors of 12 and 24 are all the factors of 12.
What is the greatest common factor of 9 and 27?
Since 27 is the multiple of 9, 9 is a factor of 27. Thus, the greatest common factor between 9 and 27 is 9.
The common factor of the two numbers is 6. if one number is 12, then which of the following could be the other number?
Out of the given option, only 18 has 6 as a factor. Hence, the other number is 18.
The only common factor between two numbers, A and B, is 1. Which of the following is always true about A and B?
Co-prime numbers have only one common factor between them. For example, 4 (an even square number) and 7 (prime number) are co-prime.
Frequently Asked Questions
What is the common factor of two prime numbers?
Prime numbers have only two factors, one and the number itself. So, the common factor between any two prime numbers is always 1.
What is a common multiple?
A common multiple is defined as a whole number, a shared multiple of each set of numbers. The multiples common to two or more numbers are called the common multiples of those numbers.
24 is a common multiple of 6 and 4. 24 is evenly divisible by both 6 and 4.
What is the smallest or least common factor of any two or more numbers?
1 is a factor of every number. So, all numbers have 1 as a common factor, which is also their least common factor.




































