CONTENT TYPE
SUBJECT
- Number Sense (44)
- Addition (42)
- Subtraction (28)
- Multiplication (63)
-
Multiplication Strategies
(5)
- Times Tables (10)
- Multiplication Properties (6)
-
Multiply By Multiples Of 10
(5)
- Multi-Digit Multiplication (36)
- Division (81)
-
Fractions
(126)
-
Fractions Using Models
(12)
-
Fractions On A Number Line
(7)
-
Compare Fractions
(13)
-
Equivalent Fractions
(25)
-
Mixed Numbers As Improper Fractions
(4)
- Fractions Operations (60)
- Decimals (81)
- Read And Write Decimals (31)
-
Compare Decimals
(16)
-
Order Decimals
(12)
-
Round Decimals
(9)
-
Convert Decimals To Fractions
(7)
- Decimal Operations (8)
- Geometry (39)
- Measurement (61)
- Money (10)
- Algebra (25)
- Word Problems (24)
Equivalent Fractions Using Models Games
View all 10 games-
VIEW DETAILS
 Equivalent Fractions Using Models
Equivalent Fractions Using ModelsAre the Fractions Equivalent Game
In this exciting math game, kids will explore equivalent fractions using visual models. They'll solve engaging problems to determine if fractions are equivalent, building a solid understanding of fractions. This interactive approach helps make learning fractions fun and intuitive, boosting confidence in math skills. Get started on mastering fractions today!
-
VIEW DETAILS
 Equivalent Fractions Using Models
Equivalent Fractions Using ModelsIdentifying Equivalent Fractions Game
Unravel the mystery of equivalent fractions with this engaging game! Using fraction strips as visual aids, kids will identify if fractions are equivalent while having fun. This interactive math adventure helps clear misconceptions and builds strong fraction skills. Perfect for young learners eager to explore fractions in a playful way. Get started now!
-
VIEW DETAILS
 Equivalent Fractions Using Models
Equivalent Fractions Using ModelsCompleting Equivalent Fractions Game
This exciting game helps third graders master equivalent fractions by using fraction strips. Kids will tackle various problems, boosting their math skills while having fun. With visual aids, students can easily grasp the concept of equivalent fractions. Perfect for young learners to enjoy and learn fractions in a playful way!
-
VIEW DETAILS
 Equivalent Fractions Using Models
Equivalent Fractions Using ModelsGenerating Equivalent Fractions Game
Unlock the mystery of equivalent fractions in this vibrant game! Kids will use visual models to practice creating fractions that are equivalent. This interactive experience makes understanding fractions fun and engaging, helping kids gain confidence in math. Watch as they explore, learn, and master the skill of generating equivalent fractions with ease.
All Equivalent Fractions Games
-
VIEW DETAILS
 Equivalent Fractions Using A Number Line
Equivalent Fractions Using A Number LineGenerating Equivalent Fractions Using Number Line Game
In this engaging math game, kids will dive into the world of fractions by generating equivalent fractions using number lines. They'll tackle problems that challenge them to fill in missing parts, boosting their understanding of fractions. It's a fun and interactive way to grasp equivalent fractions, making math both exciting and educational for young learners.
-
VIEW DETAILS
 Equivalent Fractions Using A Number Line
Equivalent Fractions Using A Number LineGenerating Multiple Equivalent Fractions Game
Unlock the world of fractions in this exciting game! Kids will use number lines to find and generate equivalent fractions, reinforcing their understanding of this key math concept. With engaging patterns and interactive play, your child will gain confidence in fractions while having fun. Perfect for young learners eager to practice and improve their math skills!
-
VIEW DETAILS
 Equivalent Fractions Using Models
Equivalent Fractions Using ModelsIdentifying the Equivalent Models Game
In this fun math game, kids tackle equivalent fractions by identifying matching visual models. Perfect for third graders, it helps clear up common misconceptions and builds strong problem-solving skills. This interactive experience guides learners towards fraction mastery while making math enjoyable. Get ready to explore fractions in a whole new way!
-
VIEW DETAILS
 Equivalent Fractions Using Models
Equivalent Fractions Using ModelsRecognizing Equivalent Fractions Game
Enter the enchanting realm of jellies and discover how to recognize equivalent fractions! This game invites kids to solve intriguing problems using visual models, reinforcing their understanding of fractions. Perfect for curious minds, it helps children apply prior knowledge to complete whole fractions in a fun, engaging way. Let the adventure begin!
-
VIEW DETAILS
 Equivalent Fractions Using Models
Equivalent Fractions Using ModelsFinding Equivalent Fractions Game
Join the adventure of finding equivalent fractions by collecting magic potions from jellies! This engaging game uses fraction models to make learning fractions fun and easy. Your child will gain confidence in math both in school and beyond. With regular play, understanding fractions becomes a breeze. Perfect for young math enthusiasts eager to explore!
-
VIEW DETAILS
 Equivalent Fractions Using Models
Equivalent Fractions Using ModelsMatching Equivalent Fractions Game
Join the adventure and learn fractions by matching jellies to create magical potions! This engaging game helps kids grasp the concept of equivalent fractions using visual models. As they play, children will enhance their understanding of fractions in a fun and interactive way. Perfect for young math enthusiasts eager to explore the world of numbers. Get started now!
-
VIEW DETAILS
 Equivalent Fractions Using Models
Equivalent Fractions Using ModelsColoring Parts to Show Tenths as Hundredths Game
In this engaging game, kids will color parts of shapes to understand how tenths can be shown as hundredths. Through interactive fraction models, they learn to relate tenths and hundredths, boosting their comfort with decimals. Perfect for making tricky concepts like equivalent fractions easier to grasp. Watch your child become a decimals whiz!
-
VIEW DETAILS
 Equivalent Fractions Using Models
Equivalent Fractions Using ModelsShade Parts to Showing Hundredths as Tenths Game
In this fun math game, kids will shade parts to show how hundredths relate to tenths. By playing, they'll tackle misconceptions about equivalent fractions and learn to model them visually. This interactive experience makes understanding fractions with denominators of 10 and 100 an enjoyable task. Perfect for fourth graders eager to boost their decimal skills!
-
VIEW DETAILS
 Equivalent Fractions
Equivalent FractionsChoosing the Equivalent Fraction Game
In this engaging math game, students will dive into the world of equivalent fractions. They'll tap interactive elements to choose the correct fraction, enhancing their understanding of fractions. Designed for young mathematicians, this game offers a fun way to practice and master the skill of generating equivalent fractions. Perfect for hands-on learning!
-
VIEW DETAILS
 Equivalent Fractions
Equivalent FractionsSelecting a Pair of Equivalent Fractions Game
In this fun math game, your child will select pairs of equivalent fractions, helping them tackle common misconceptions. Designed for fourth graders, it strengthens fraction skills by letting young mathematicians practice generating and identifying equivalent fractions. Kids will enjoy learning math concepts while playing this exciting game!
-
VIEW DETAILS
 Equivalent Fractions
Equivalent FractionsFilling in to Show Equivalence Between Tenths and Hundredths Game
This engaging math game helps kids relate tenths to hundredths, building a strong understanding of decimals. Through fun tasks, your child will learn to connect fractions with decimals effortlessly. Perfect for young learners eager to master decimal notation. Watch your fourth grader enjoy learning while boosting their math skills. Start for free!
-
VIEW DETAILS
 Equivalent Fractions
Equivalent FractionsFilling in to Complete the Equivalent Fractions Pattern Game
In this fun math game, kids will complete patterns using equivalent fractions. By filling in the missing parts, they'll gain confidence in identifying and generating equivalent fractions. This interactive activity helps make a tricky concept more approachable and enjoyable, allowing children to practice and solidify their fraction skills with ease.
-
VIEW DETAILS
 Equivalent Fractions
Equivalent FractionsAdding Decimal Fractions Using Equivalence Game
This exciting game helps your child master adding decimal fractions using equivalence. Through playful activities, kids will learn to add tenths and hundredths, making math fun and easy. Designed for fourth graders, the game transforms learning fractions into an engaging adventure. Perfect for building confidence in handling fractions with denominators 10 and 100. Get started today!
-
VIEW DETAILS
 Equivalent Fractions
Equivalent FractionsCompleting the Equivalent Fractions Game
In this engaging math game, kids will tackle problems on equivalent fractions by identifying the missing parts. Perfect for young mathematicians, this game makes learning fractions lively and fun. As they play, children will explore the concept of equivalent fractions, boosting their math skills in an interactive way.
-
VIEW DETAILS
 Equivalent Fractions
Equivalent FractionsFill the Blank to Make an Equivalent Fraction Game
In this exciting math game, your child will fill in the blanks to create equivalent fractions. Designed for fourth graders, this game offers a variety of problems to help kids practice and understand fractions in a fun way. Boost their confidence and skills as they explore and generate equivalent fractions. Perfect for young math enthusiasts!
-
VIEW DETAILS
 Equivalent Fractions
Equivalent FractionsMultiplying and Completing the Equivalent Fraction Game
Uncover the world of equivalent fractions with this interactive game. Kids will multiply fractions to discover their equivalents, overcoming common misconceptions. This game offers a fun and focused approach to mastering fraction skills, making learning both enjoyable and effective. Perfect for young mathematicians eager to enhance their math journey.
-
VIEW DETAILS
 Equivalent Fractions
Equivalent FractionsSelecting the Pair of Equivalent Fractions Game
Jump into the fun of fractions! In this game, kids will select pairs of equivalent fractions from given options, honing their fraction skills. Perfect for young math explorers, this game boosts confidence in identifying equivalent fractions without visual aids. An exciting way to practice and master the concept of fractions. Get ready to play and learn!
-
VIEW DETAILS
 Equivalent Fractions
Equivalent FractionsSelecting the Correct Equivalent Expression Game
In this fun math game, kids practice identifying equivalent fractions. They'll tackle problems using their understanding to find the correct expressions. Perfect for making learning lively, this game boosts skills in fractions while ensuring a fun experience. Ideal for fourth graders who want to learn while having a blast!
-
VIEW DETAILS
 Equivalent Fractions
Equivalent FractionsDividing and Completing the Equivalent Fraction Game
Get ready to explore the world of fractions with this engaging game! Kids will learn to divide and generate equivalent fractions, building a strong understanding of this crucial math concept. Perfect for young learners, this game turns complex ideas into fun exercises, boosting confidence and skills in fractions. Watch your child become a fraction whiz!
-
VIEW DETAILS
 Equivalent Fractions
Equivalent FractionsFilling in the Number That Makes Tenths and Hundredths Equivalent Game
This engaging math game lets kids solve problems and fill in numbers to make tenths and hundredths equivalent. By tapping interactive elements, young learners will master the concept of equivalent fractions with denominators 10 and 100. It's a fun way to practice decimals while enhancing problem-solving skills. Perfect for building confidence in math. Signup now!
-
VIEW DETAILS
 Equivalent Fractions
Equivalent FractionsFilling in to Make Tenths and Hundredths Equivalent Game
This interactive math game invites kids to explore the world of fractions and decimals by filling in models to make tenths and hundredths equivalent. Through active participation, children will practice and improve their understanding of equivalent fractions. Perfect for young learners eager to grasp the concepts of decimals and fractions in an engaging way.
Your one stop solution for all grade learning needs.
Give your child the passion and confidence to learn anything on their own fearlessly





















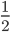 and
and 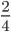 . Though the denominators and numerators look different, the value of both the fractions is the same. They are called equivalent fractions.
. Though the denominators and numerators look different, the value of both the fractions is the same. They are called equivalent fractions.
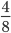 .
.

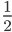 if you simplify fractions given in the area models.
if you simplify fractions given in the area models.




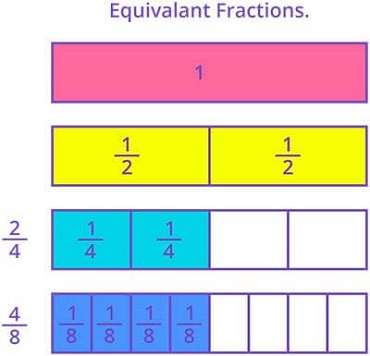
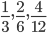 are equivalent fractions. The area shaded in all the three fractions are equal. Though they are expressed differently, the value of all the three is the same.
are equivalent fractions. The area shaded in all the three fractions are equal. Though they are expressed differently, the value of all the three is the same.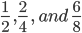 .
.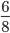 is not equivalent to the other two.
is not equivalent to the other two.
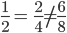 .
. are plotted on a number line, they occupy the exact same point.
are plotted on a number line, they occupy the exact same point.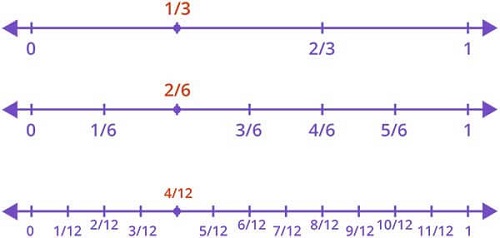
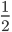 and
and 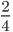 by simply doubling or tripling the numerators and denominators. At this level, the equivalent fractions worksheets available at
by simply doubling or tripling the numerators and denominators. At this level, the equivalent fractions worksheets available at 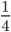 . This can be represented using area model as shown.
. This can be represented using area model as shown.

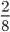 and it is equivalent to the unit fraction
and it is equivalent to the unit fraction 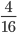 as shown:
as shown: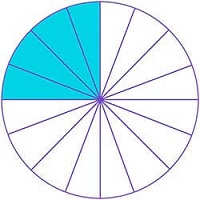
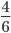 .
.

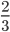 .
.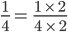 =
= 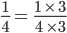 =
= 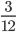 .
.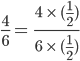 =
= 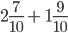
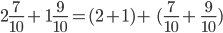
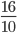
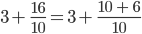
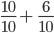
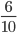
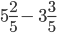 .
.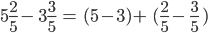
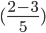
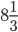 , can be converted to an equivalent fraction as follows:
, can be converted to an equivalent fraction as follows:
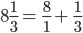
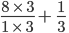
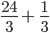
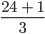
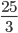
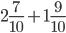 .
.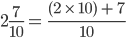 =
= 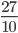
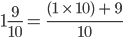 =
= 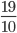
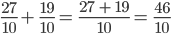
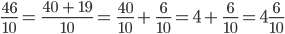
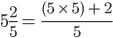 =
= 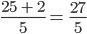
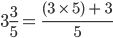 =
= 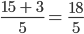
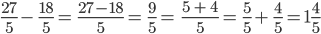

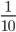 with a denominator 100?
with a denominator 100?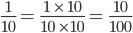

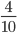 and
and 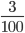 , first rewrite
, first rewrite 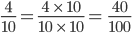
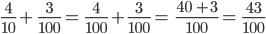
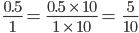
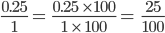
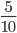 and
and 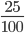 the two fractions do not have the same whole. To compare them, rewrite the first fraction.
the two fractions do not have the same whole. To compare them, rewrite the first fraction.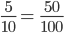
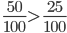 .
.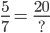 . Ans: 28
. Ans: 28