What Is Additive Comparison?
Word problems that compare two amounts by stating how much more (or less) one amount is than the other are included in the additive comparison.
In math, checking if a number is smaller, greater, or equal to another number is known as comparison.
For example, Zyna has $\$16$ and Diana has $\$20$.
Since $20 \gt 16$, we can say that Diana has more money.
Recommended Games
Additive Comparison: Definition
We find the relation between two amounts by asking how much more or less one amount is compared to the other. In other words, an additive comparison problem is a problem in which:
- Two verbal statements are used to compare two sets of items, and
- Further, an additive equation is determined.
- The equation includes numbers and the alphabet, or the variable.
An example of an additive comparison problem using the equation is given below:
Daisy takes 20 minutes to reach school from her home. Ryan takes 15 more minutes than Daisy and Sheryl takes 5 more minutes than Ryan. How much time does Sheryl take to reach school?
Time taken by Daisy to reach school $= 20$ minutes
Time taken by Ryan $= 5$ minutes more than Daisy $= 20 + 15 = 35$ minutes
Time taken by Sheryl $= 35 + 5 = 40$ minutes
Therefore, Sheryl takes 40 minutes to reach school.
Words used in additive comparison are:
- How many more
- How many less
- More than (8 more than 42 miles)
- Less than (6 less than 32 liters)
Recommended Worksheets
What Is a Bar Model?
In math, a bar model is defined as a pictorial representation of a number in the form of bars used to solve number problems. It helps us to attain an understanding of how a problem needs to be solved and calculated.
For instance, one rectangle of the bar model represents a value of 6. We have to find 3 times the value of one bar. So, the value of bar model $= 6 \times 3 = 18$.
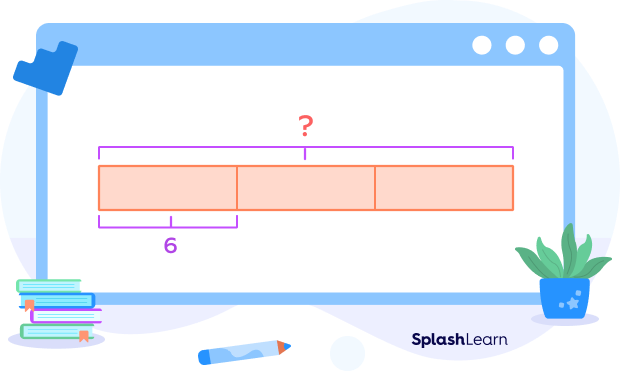
It helps us understand which arithmetic operations are used to solve a word problem. Here’s how we can represent different operations using bar models.

In the image (A), the first bar is of 60 and the second is of 30. The bar given below will give us $60 + 30 = 90$.
We are aware of the fact family.
$60 + 30 = 90$, so the subtraction equation will be: $90 \;–\; 30 = 60$
Comparison Word Problems
There are three types of additive comparison word problems:

- Difference is unknown
Connie has 12 red marbles and 23 blue marbles. How many more blue marbles than red marbles does Connie have?
This is a subtraction problem.
$23 \;-\; 12 = 11$
- Unknown quantity is big
Connie has 12 red marbles and some blue marbles. She has 15 more blue marbles than red ones. How many blue marbles does Connie have?
This is an addition problem.
$12 + 15 = 27$
- Unknown quantity is small
Connie has 20 blue marbles. She has 17 more blue marbles than red ones. How many red marbles does Connie have?
This is a subtraction problem.
$20 \;–\; 17 = 3$
Let’s solve a few additive comparison problems using bar models.
Example 1: Kate has 7 stamps. Sara has 5 more. How many stamps does Sara have?
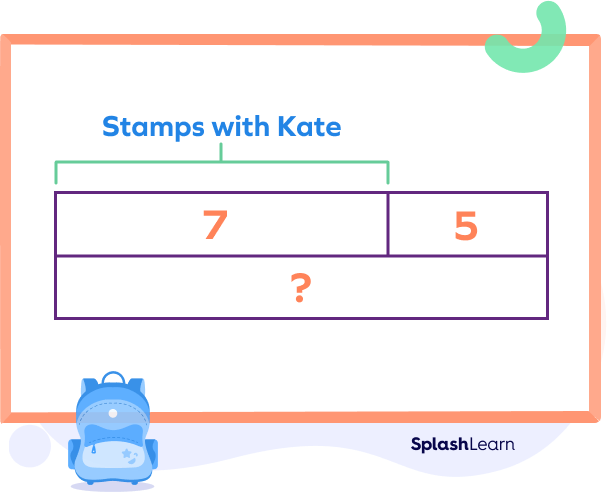
Stamps with Kate $= 7$
Stamps with Sara $= 7 + 5 = 12$.
Therefore, Sara has 12 stamps
Example 2: Jack scored 22 points in a game. Jim scored 6 less points than Jack. How many points did Jim score?
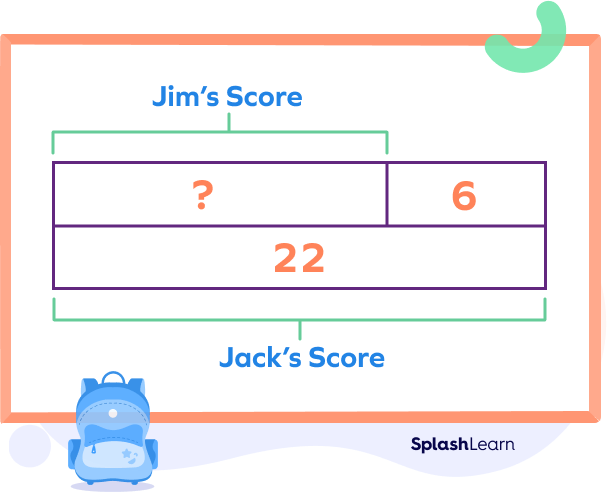
Points scored by Jack $= 22$
Points scored by Jim $= 6$ less than Jack $= 22 \;–\; 6 = 16$
Therefore, Jim scored 16 points.
Additive Comparison of Decimal Numbers
Decimal numbers are the numbers whose whole part and fractional part are separated using a decimal point. For example: 2.34.
Finding the additive comparison of decimal numbers is the same as finding the additive comparison of whole numbers.
Marie has $\$2.45$ and Myra has $\$1.14$ more than Marie. How much money does Myra have?
Amount of money with Myra $= \$2.45 + \$1.14 = \$3.59$
Solved Examples On Additive Comparison
1. In a basketball game, Peter scored 22 baskets on Monday. He scored 13 more baskets on Tuesday. Find the number of baskets he scored on Tuesday using the bar model.
Solution:
Baskets scored on Monday $= 22$
Baskets scored on Tuesday $= 13$ more baskets than Monday
The bar model is given by:
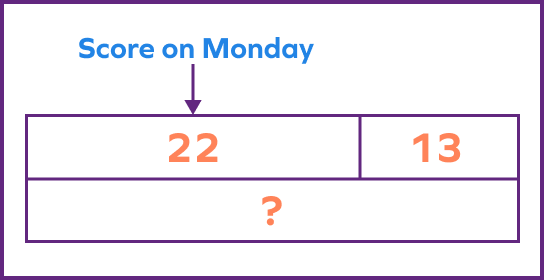
Number of baskets scored on Tuesday $= 22 + 13 = 35$
2. Sophie has 45 marbles and Mia has 32 marbles. Who has more marbles?
Solution:
Since $45 \gt 32$, Sophie has more marbles.
Difference $= 45 \;–\; 32 = 13$
Sophie has 13 more marbles than Mia.
3. There were 12 less girls than the number of boys in a summer camp. If the number of boys were 58, how many girls were there? (Use the bar model.)
Solution:
The bar model is given by:
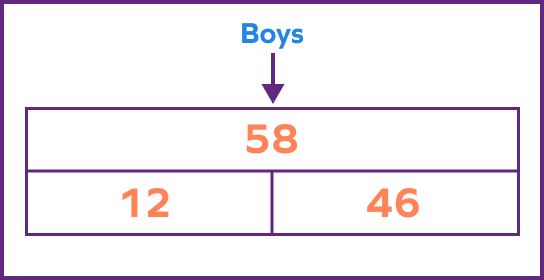
Number of girls $= 58 \;–\; 12 = 46$
4. On Monday, the temperature was $65.6^{\circ}\text{F}$ and on Tuesday, the temperature was $6.2^{\circ}\text{F}$ more than Monday. What was the temperature on Tuesday?
Solution: Temperature on Monday $= 65.6^{\circ}\text{F}$
Temperature on Tuesday $= 65.6^{\circ}\text{F} + 6.2^{\circ}\text{F} = 71.8^{\circ}\text{F}$
Practice Problems On Additive Comparison
Additive Comparison - Definition with Examples
What will replace “?” in the given model?
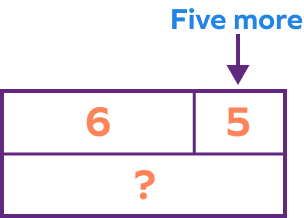
$? = 6 + 5 = 11$
Oliver has 25 books. Peter has 7 more books. How many books does Peter have?
Number of books with Peter $= 25 + 7 = 32$
Cayla did 72 sit ups in the morning. Nekira did 48 sit ups at night. How many more sit ups did Cayla do than Nekira?
More sit-ups that Cyla did than Nekira $= 72 \;–\; 48 = 24$
Kitty has $\$450$ out of which she used $\$215$ to buy a scooter. How much money is she left with?
Amount Kitty had $= \$450$
Amount she gave $4= \$215$
Amount left $= \$450 \;–\; \$215 = \$235$
Adam has 15 lollipops less than Hope. If Adam has 29 lollipops, how many lollipops does Hope have?
Number of lollipops with Adam $=$ Number of lollipops with Hope $–\; 15$
$29 =$ Number of lollipops with Hope $–\; 15$
Number of lollipops with Hope $= 29 + 15 = 44$
Frequently Asked Questions On Additive Comparison
What is the difference between addition and additive comparison?
Addition means to add two or more numbers and to find the sum. Whereas additive comparison is to find the relation between two amounts by identifying how much more or less one amount is one compared to the other.
What is the difference between additive comparison and multiplicative comparison?
Additive comparison is to find the relation between two amounts by asking or telling how much more or less one amount is one compared to the other. Multiplicative comparison is to compare two quantities such that when one is multiplied by a specified number, the other is produced.
What is comparison subtraction?
In comparison subtraction, we subtract to find out how much bigger (or how much smaller) one set is compared to another. It is the same as additive comparison.
How does additive comparison work in fraction?
We divide the bar into equal parts which is the denominator of the first fraction and then shade the numerator. Then, we convert the same bar as per the denominator of the second fraction and delete the bars as per given in the numerator of the second fraction.




































