Reasonableness in Math

Reasonableness: Introduction

Have you ever come across a situation where you are attempting a math problem and need to check whether you did it right or not? When you find the solution, a good way to check if the problem is solved correctly is to check for reasonableness. 

While solving a problem, you should always ask yourself whether your answer is logical and appropriate or simply whether it makes sense or not.

Let’s see how we can use the concept of reasonableness.

What Is Reasonableness in Math?

What does reasonable mean in math? Well, all it means is being moderate or fair while finding a solution and not excessive than the actual number or what is reasonable within the context of the given factors or values. This is the simple meaning of reasonableness.

When solving a math problem, we can check if the answer we have derived is reasonable or not, based on an estimate. A reasonable estimate does not exceed the original numbers in a problem. Let us look at a reasonable estimate example:

Example 1: Suppose you want to divide $\$418$ among 4 people. What would be the reasonable estimate? 

We can round down 418 to the nearest hundreds, 420.

$420 \div 4=105$

Actual answer $= 104.5$

Thus, our solution is reasonable.

Example: Find $65 − 29$.

Actual subtraction:

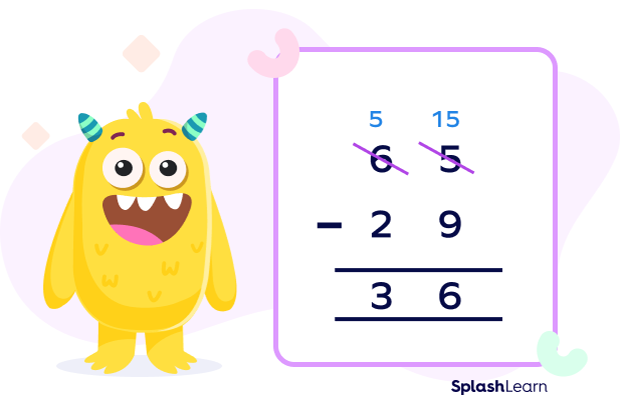
So, $65 − 29 = 36$

How would you check if it is reasonable or correct?

Add 36 and 29. 

$36 + 29 = 65$

So, the answer is correct!

Reasonableness: Definition

In math, reasonableness can be defined as checking or verifying whether the result of the solution or the calculation of the problem is correct or not. We can do it by either estimating or plugging in your result to check it. 

We use convenient numbers to find an estimate and then compare this estimate to the actual answer to check for reasonableness. Sometimes, this method may not tell you if you have the correct answer, but it will definitely tell you if you are close.

How Do You Calculate Reasonableness?

There are various situations where we use reasonableness. We use it to cross-verify our addition, multiplication, division, and even other complex mathematical problems. 

How to Verify Multiplication

Students often make mistakes while carrying out multiplication of two large numbers. This method helps gain confidence and makes sure that the answer is not outrageous.

For example, let’s multiply 51 and 41.

In the first step, round 51 to 50 and 41 to 40. 

Multiply 50 and 40.

$50 \times 40 = 2000$.

The actual product is given by

$50 \times 40 = 2091$.

Now we subtract 2000 from 2091, the answer will be 91.

This shows that the difference between them is very less; thus, our answer is correct. If we had got a more considerable difference, then we would have had to consider it wrong.

How to Verify Division Problems

We can solve and verify the division problems using estimation. Round the divisor and the dividend to the closer and convenient value and check whether the actual answer is reasonable or not.

For example, let’s find the answer to $\frac{2100}{1518}$. 

1. Round up the dividend to 2000 and the divisor to 1500. 
2. Here you can estimate that the solution to $\frac{2000}{1500}$ will be close to 1 because $\frac{20}{15} \approx 1.3$
3. After doing the actual calculation for $\frac{2100}{1518}$, the answer is about 1.35.

Sometimes try to look for patterns that are familiar to you and can help you in solving different problems. 

For example, let’s solve $\frac{63}{7}$. 

1. The square of 8 is 64; this will allow you to estimate the approximate value quickly to 8. 
2. Here, the actual answer is 9, which is very close to 8.

We can examine the divisor, simply it and check for multiples that are close to the value of the dividend. 

For example, in $\frac{8544}{45}$, there are two options: 

1. If you are rounding the dividend to 9000, then your estimate for the quotient will be 200 based on $45 \times 200 = 9000$
2. If you are rounding the divisor to 50, then the estimate will be 171 on the basis of $171 \times 50 = 8550$.

 The actual quotient is 189.8. So, both the estimates are valid; we can use either.

Fun Facts!

• Rounding numbers, making numbers compatible, and properties of operations are some strategies that are used to check the reasonableness of answers.

Conclusion

In this article, we learned about the concept of reasonableness. We came across some conditions like multiplication and division and how we use reasonableness in such cases. We can now look at some examples and solve some practice problems to better understand reasonableness. 

Solved Examples

1. Solve $45 \times 5$ using reasonableness.

Solution: 

On calculating $45 \times 5$, we get 225. Now, for the sake of reasonableness, if we divide 225 by 5, 

We get

$\frac{225}{5} = 45$. 

Hence, we verified using reasonableness.

2. Anne bought 3.8 pounds of grains. The grains cost her $\$1.99$ per pound. What was the total cost of Anne’s grains? Also, find a reasonable estimate.

Solution:

The grains cost $\$1.99$ per pound.

To find the cost of 3.8 pounds, we have to multiply 1.99 and 3.8 as represented below.

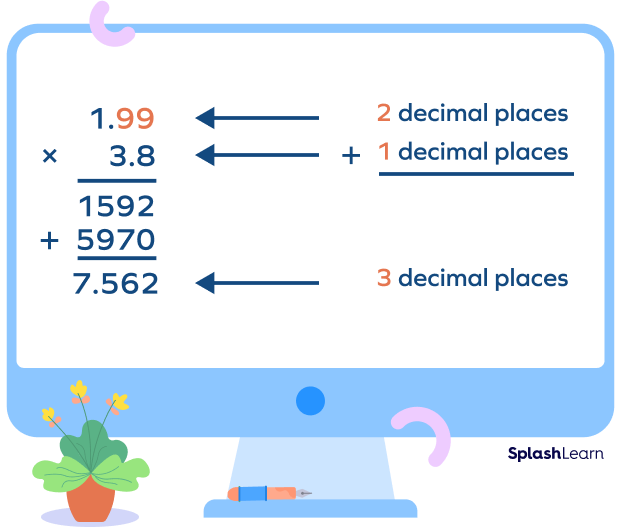
If we round the answer 7.562 to the nearest hundredth place, we get 7.56.

Hence, the cost of 3.8 pounds of grains is $\$7.56$.

Now, let us find a reasonable estimate.

Round 1.99 to the nearest whole number, that is, 2.

Round 3.8 to the nearest whole number, that is, 4. 

Multiplying the whole numbers 2 and 4.

That is, $2 \times 4 = 8$

The answer is reasonable, because 8 is close to 7.56.

3. A certain plant grows 3.75 inches per month. If the plant continues to grow at this rate, how much will the plant grow in 6.25 months ?

Solution:

A certain plant grows in one month  $=  3.75$ inches.

To find the amount of plant grown in 6.25 months, we have to multiply 3.75 and 6.25 as given below. 

Hence, the plant will grow 23.4375 inches in 6.25 months.

Now, let us estimate to check if our answer is reasonable.

Round off 3.75 to the nearest whole number, that is, 4.

Round off 6.25 to the nearest whole number, that is, 6. 

Multiply the whole numbers 4 and 6, that is, $4 \times 6 = 24$

Our answer is reasonable, because 24 is closer to 23.437.

4. Tanya bought 3.4 pounds of yogurt that cost $\$6.95$ per pound. How much did she spend on yogurt?

Solution:

The cost of one pound of yogurt $=  \$6.95$

To find the cost of 3.4 pounds of yogurt, we have to multiply 3.4 and 6.95.

$3.4 \times 6.95  =  23.63$

Hence, the cost of 3.4 pounds of yogurt is $\$23.63$

Now, let us estimate to check whether our answer is reasonable.

Rounding off 3.4 to the nearest whole number-

That is, 3

Rounding off 6.95 to the nearest whole number-

That is, 7 

Multiplying the whole numbers 3 and 7.

That is, $3 \times 7  =  21$

Our answer is reasonable. Because 21 is much closer to 23.63.

5. Cameron earns $\$9.40$ per hour working at a dairy farm. How much money will he earn for 18.5 hours of work ?

Solution:

Cameron’s earning in one hour  $=  \$9.40$

To find his earning of 18.5 hours, we have to multiply 18.5 and 9.40

$18.5 \times 9.4  =  173.90$

Hence, his earning for 18.5 hours is $\$173.90$.

Now, let us estimate to check if our answer is reasonable.

Rounding off 18.5 to the nearest whole number, that is, 19.

Rounding off 9.40 to the nearest whole number, that is, 9. 

Multiplying the whole numbers 19 and 9.

That is, $19 \times 9 = 171$

Our answer is reasonable. Because 171 is much closer to 173.90

Practice Problems

Frequently Asked Questions