What Are the Different Types of Triangles?
A triangle is a closed 2-dimensional shape with three sides. There are mainly 6 different types of triangles.
- Based on the lengths of the sides, there are three types of triangles: scalene, isosceles, and equilateral triangles.
- Based on the measures of its interior angles, there are three types of triangles: acute (if all angles are less than 90°), right (if one angle is 90°), and obtuse (if one angle is more than 90°)
The figure given below shows 6 types of triangles and their properties.
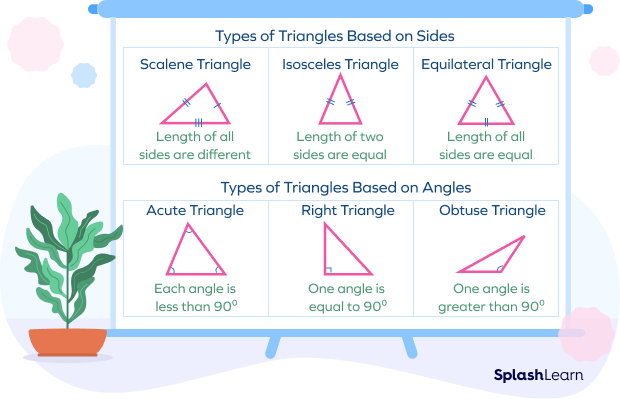
Recommended Games
What Is the Classification of Triangles?
As mentioned earlier, triangles can be classified easily based on the measurement of sides and angles. Triangles can also be classified based on the measurement of both sides and angles. Three ways of classification are:
- Based on the lengths of the three sides
- Based on the measurement of three angles
- Based on the measurement of sides and angles
A triangle has three sides, interior angles, and vertices. There are different names for triangles depending on the type of classification. These names have the keywords that express the nature and properties of the triangle.
Take a look at the table below to understand triangle classification and the different names of triangles.
| Classification of Triangles | ||
|---|---|---|
| Based on sides | Based on sides and angles | Based on sides and angles |
| Equilateral Triangle | Acute Triangle | Equiangular Triangle |
| Isosceles Triangle | Right Triangle | Isosceles Right Triangle |
| Scalene Triangle | Obtuse Triangle | Obtuse Isosceles Triangle |
| Acute Isosceles Triangle | ||
| Right Scalene Triangle | ||
| Obtuse Scalene Triangle | ||
| Acute Scalene Triangle | ||
Recommended Worksheets
What Is a Triangle?
A triangle is a polygon with three sides. The point where two sides of the triangle meet is called the vertex and forms an interior angle. All triangles have three sides, three vertices, and three interior angles.
Consider a triangle △ABC with three vertices: A, B, and C.
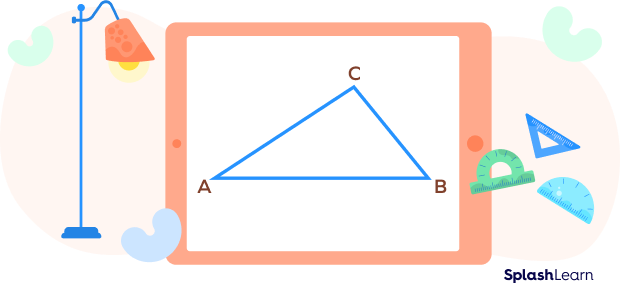
Basic Properties of Triangles
- A triangle has three interior angles, and the sum of all the interior angles in a triangle is 180°. This is known as the angle-sum property of a triangle.
- A triangle has three sides. The sum of the lengths of any two sides of a triangle is greater than the measure of the third side. This is also known as the triangle inequality property.
- The longest side of the triangle is opposite its biggest angle, and the side opposite the smallest angle is the shortest side of the triangle.
Classification of Triangles Based on Side Lengths
There are 3 types of triangles based on the measure of their sides. We classify the triangles by their sides as equilateral, isosceles, and scalene.
- Scalene Triangles
All sides of a scalene triangle are of different lengths. Consequently, the three interior angles are different from each other.
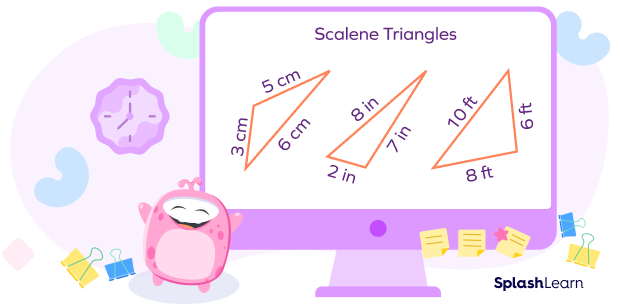
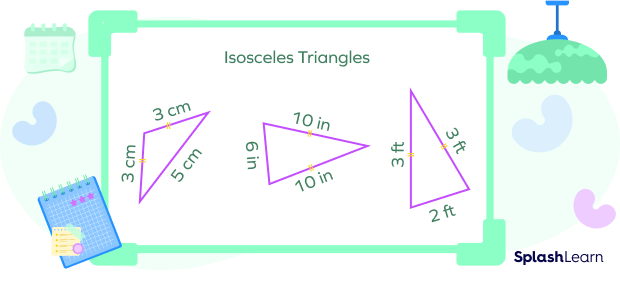
- Isosceles Triangles
An isosceles triangle has two sides of equal length. The angles opposite to these equal sides are equal.
Two equal sides are known as the legs of the triangle, and the angle formed between them is called the vertex angle.
- Equilateral Triangles
The three sides of an equilateral triangle are of equal length. Consequently, each interior angle of equilateral triangles is equal to 60°. It is a regular polygon; as the name suggests, it has equal sides and angles.
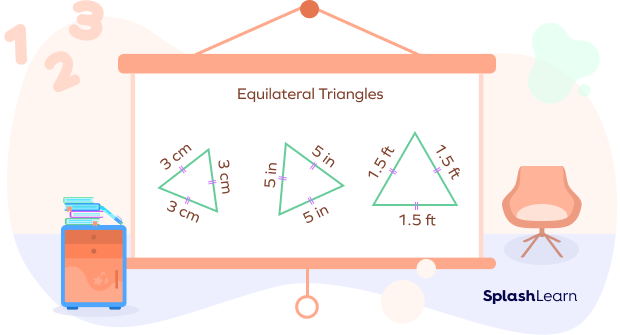
Let’s quickly summarize!
We classify the triangles by their sides as equilateral, isosceles, and scalene.

Classification of Triangles Based on Interior Angles
In geometry, there are various types of angles based on measurement. The interior angles of a triangle can be of three kinds: acute, right, or obtuse.
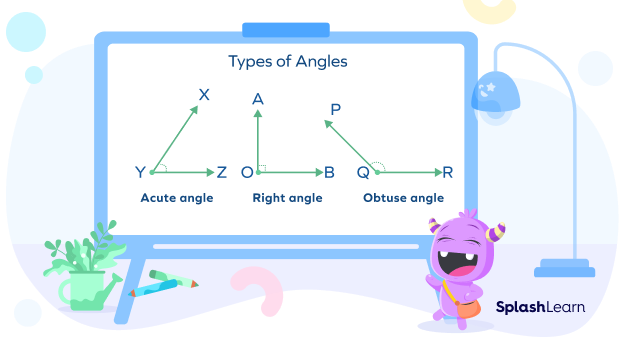
Another way to study the classification of triangles is based on angles. As is apparent, every triangle has three angles. The sum of the measures of these angles is 180 degrees. Based on the measure of interior angles, there are three types of triangles.
- Acute Triangles:
All interior angles in an acute triangle are acute angles. Each interior angle measures less than 90°. Thus, an acute triangle is formed when all three interior angles of a triangle measure less than 90 degrees. Its sides may or may not be equal.
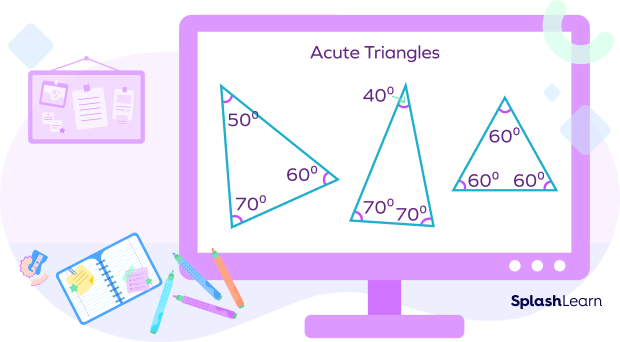
- Right Triangles
A right triangle is one in which at least one of the angles is 90 degrees, and the other two angles are acute. This angle is called a right angle. According to Pythagoras’ theorem, the side of the triangle opposite the right angle is the longest in the right triangle. It is called the hypotenuse.
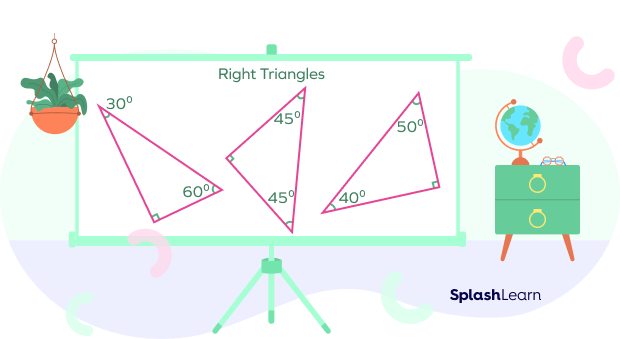
- Obtuse Triangles
A triangle with one interior angle greater than 90° or an obtuse angle is called an obtuse triangle. In this case, one of the angles of the triangle is larger than 90 degrees and the sum of the other two angles in the triangle is less than 90 degrees.
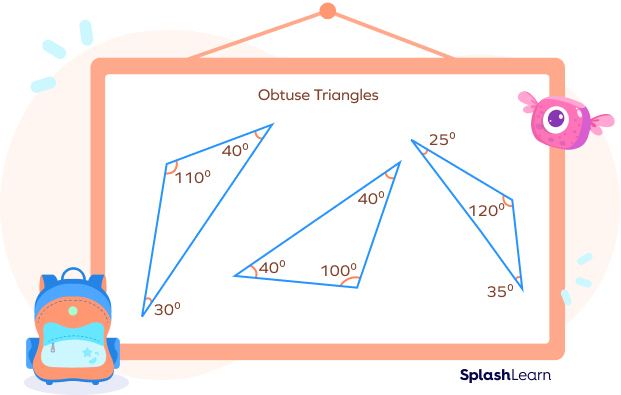
Let’s summarize! Take a look at the image showing the triangle classification by angles.
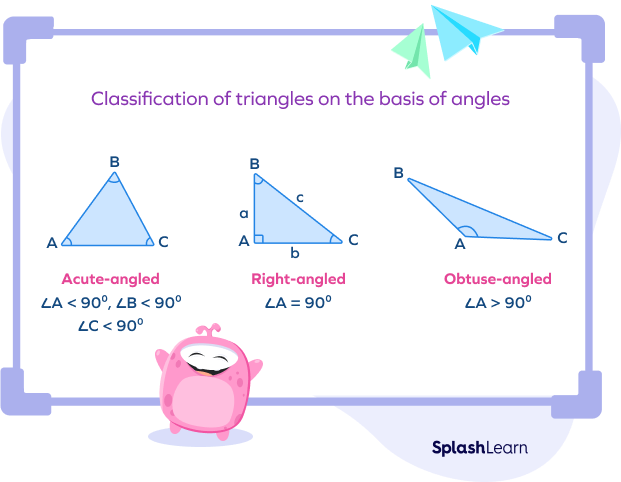
Classification of Triangles Based on Angles and Sides
Classification of triangles can be done based on the sides and angles of the triangle.
- Equiangular Triangle: An equiangular triangle is one in which all the sides are of equal lengths, and all the triangle angles are of equal measure. It is also known as an equilateral triangle.
- Isosceles Right Triangle: In an isosceles right triangle, two sides of a triangle are equal, and any one angle of the triangle is equal to 90 degrees. The two remaining angles are congruent.
- Obtuse Isosceles Triangle: An obtuse isosceles triangle has two sides that are equal and one angle that is obtuse.
- Acute Isosceles Triangle: In this type of triangle, all three angles are acute, and any two sides of the triangle are equal.
- Right Scalene Triangle: A right scalene triangle is one in which any of the angles is a right angle, and all the sides of the triangle are unequal.
- Obtuse Scalene Triangle: In this type of triangle, one of the angles is an obtuse angle, and all the sides of the triangle measure differently.
- Acute Scalene Triangle: This triangle has three unequal sides and three acute angles. So, it is called an acute scalene triangle.
Conclusion
In this article, we learned about the types of triangles. They can be classified based on their sides, angles, and both sides and angles. Let’s solve a few examples and practice problems for better comprehension.
Solved Examples on Types of Triangles
Example 1: Classify the triangle as equilateral, isosceles, or scalene.
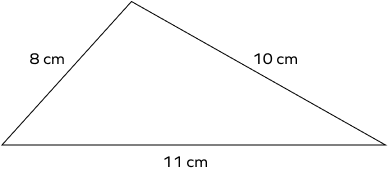
Solution:
Examine the lengths of the sides to see if any sides are equal. All sides of the triangle are different from each other.
Therefore, the triangle is scalene.
Example 2: Classify the triangle as acute, right, and obtuse.
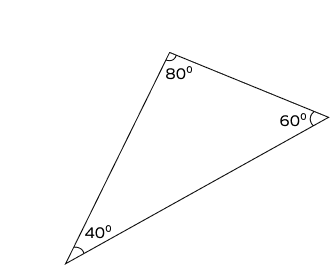
Solution:
Examine the measure of each interior angle of the given triangle and compare it to 90°. All the angles of the triangle are less than 90°.
Therefore, the triangle is acute.
Example 3: In an isosceles triangle ABC, ∠A = 100° and ∠B = ∠C. Find the measure of ∠C.
Solution:
Following the angle sum property of a triangle, we get
∠A + ∠B + ∠C = 180°
So, ∠B + ∠C = 180° – 100° = 80°
Since ∠B = ∠C, measure of ∠C = 80° ÷ 2 = 40°
Example 4: If the length of all three sides of a triangle is not equal, identify the type of triangle according to the classification of triangles.
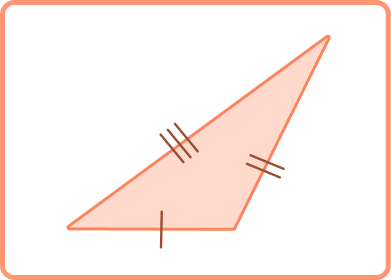
Solution: This is a scalene triangle. In this type of triangle, the lengths of the three sides are different.
Example 5: Based on the properties of a triangle, if the measure of the angle at the vertices of a triangle is 60 degrees, identify the type of triangle based on the classification of triangles.
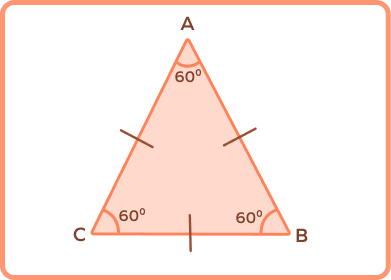
Solution: A triangle with all angles measuring 60 degrees is an equilateral triangle. An equilateral triangle is one in which all the interior angles are the same, measuring 60 degrees each. In this case, the sum of all the angles of the triangle is 180 degrees.
Example 6: If the lengths of a triangle are 4 in, 4 in, and 5 in, identify the type of the triangle.
Solution: This type of triangle is an isosceles triangle. An isosceles triangle is one in which two sides of a triangle are equal, and the third side of the triangle is different.
Practice Problems on Types of Triangles
Types of Triangles - Definition With Examples
What type of triangle is shown in the image given below?
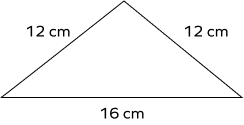
Two sides of the triangle are equal. Therefore, it is an isosceles triangle.
If the two angles of a triangle are 45° and 60°, what is the third angle? Classify the triangle.
According to the angle sum property, the third angle must be 180° - 45° - 60° = 75°
All the interior angles are less than 90°.
Therefore, the triangle is acute.
Which of the following cannot be the sides of a scalene triangle?
All sides of a scalene triangle must have different lengths.
In a right triangle, find the measure of angle B if angle A measures 30°.
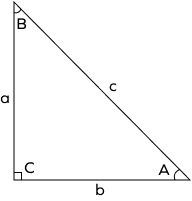
According to the angle sum property, m∠B = 180° - m∠C -m∠A = 180° - 90° - 30° = 60°
Based on the classification of triangles, which of the following combinations of angle measures will form an obtuse triangle?
In an obtuse triangle, one of the vertex angles is an obtuse angle. Among the given options, only option B consists of an obtuse angle, which is an angle exceeding 90 degrees.
If one angle of a triangle is 90 degrees, identify the type of the triangle.

A triangle with a right angle is called a right-angled triangle. It is defined based on angles when performing the classification of triangles.
Which of the following properties aptly describes a right-angled triangle?
A right-angled triangle is classified by one angle in the triangle, which measures 90 degrees. Further, the sum of the other two angles of the triangle is not more than 90 degrees, which in this case is 60 and 30 degrees.
Frequently Asked Questions about Types of Triangles
What is a triangle?
A triangle is a closed, 2-dimensional shape with three sides, three angles, and three vertices. A triangle is also a polygon.
Are interior angles of an equilateral triangle always 60°?
Yes. An equilateral triangle has three equal sides, and all three interior angles are equal. Applying the angle sum property, we can say that each angle of an equilateral triangle must be 180°÷ 3 or 60°
Can an isosceles triangle be obtuse?
An isosceles triangle has two equal sides, and angles opposite to these sides are equal. In an isosceles triangle, the equal angles are acute. The third angle can be acute, obtuse, or right. Therefore, an isosceles triangle can be an obtuse triangle.
How many right angles can a triangle have?
A triangle cannot have more than one right angle. Every triangle has to follow the angle sum property, which states that the sum of the three interior angles is 180°. We cannot construct a triangle with more than one right angle. If one angle is 90°, the other two must be acute.
Which triangle has 3 lines of symmetry?
Every equilateral triangle has three lines of symmetry. This is because each line of symmetry will always pass through a triangle’s vertex.
Which triangles have reflection symmetry?
Every equilateral and isosceles triangle has the properties of reflection symmetry. Reflection symmetry is a type of symmetry in which one half of an object reflects the other. It is also known as mirror symmetry.
How do equilateral and equiangular triangles differ from each other?
Although equilateral and equiangular triangles are regular polygons, there lies a main difference between the two. An equilateral triangle usually has congruent sides, similar to a Rhombus but an equiangular triangle has congruent interior angles like a rectangle. If a polygon satisfies the condition of both equilateral and equiangular triangles, then it is considered a regular polygon.
Is it possible for an acute triangle to be a scalene triangle?
Yes, an acute triangle can be a scalene triangle. We can always draw an acute triangle, whether it has equal sides. Only the angles of an acute triangle need to be less than 90 degrees to be called one such triangle.
What conditions do all triangles fulfill, irrespective of the type of the triangle?
Irrespective of the classification of triangles, the two conditions that all triangles satisfy are
- the sum of two sides of a triangle is greater than the third side.
- the sum of all the interior angles is 180 degrees.

































