What is Partitioning in Math? Definition with Examples

Here’s an interesting thing about math—you will need it in real-life scenarios, but you may not always have a pencil/pen and paper to solve the calculations. 

But by learning partitions in math, you can visualize mathematical problems and solve them in your head—without needing a pencil, paper, or a calculator!

You must be wondering what is Partition in Maths? Let’s see what it is and how we use it. 

What Is Partitioning in Math?

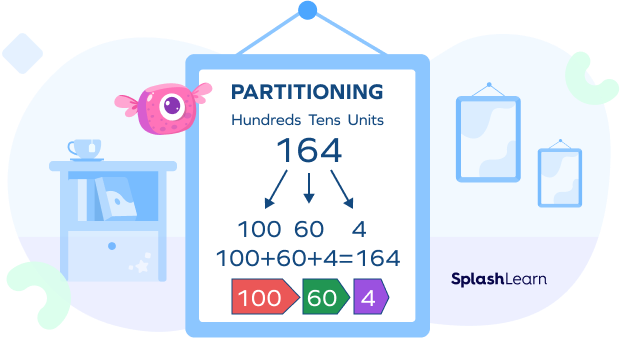
Using partitioning in mathematics makes math problems easier as it helps you break down large numbers into smaller units. We can also partition complex shapes to form simple shapes that help make calculations easier.

Partitioning Numbers

a) Addition by Partitioning

Let us think of a number like 956. Now let us add another number, 378, to it. Does this problem seem difficult to solve?

Don’t worry. You will learn a new trick to break down such numbers for easy addition.

Let us start with 956. You can partition this number as

900 + 50 + 6

Here, we have separated the numbers into units, tens, and hundreds.

Similarly, let us partition 378 into units, tens, and hundreds.

300 + 70 + 8

When you write numbers like these, you can visualize them easily in your mind and find it easier to work with them.

Now, you can break down the problem to add 956 and 378:

956 + 378

900 + 50 + 6 + 300 + 70 + 8

Upon adding the tens, units, and hundreds, we get

1200 + 120 + 8

1200 + 128

= 1328

Wasn’t that easy and fun? Let’s learn how to solve more mathematical calculations using partitions.

b) Partitioning in Subtraction

You can also use partitioning for subtracting two numbers. 

Let us understand this with an example:

Suppose you have to subtract 42 from 95, you can start by breaking the numbers into units and tens.

So, 95 = 90 + 5

and 42 = 40 + 2

95 − 42 = 90 + 5 − (40 + 2)

= 90 + 5 − 40 − 2

= 90 − 40 + 5 − 2

= 50 + 3

= 53

c) Different Ways of Partitioning Numbers

There are different ways to partition a number. One way is to divide it into hundreds, tens, and units, as we have done above. 

However, that’s not the only way.

Depending upon the numbers you are working with, you can divide numbers differently.

Let’s understand this with an example:

Take the number 104. Suppose you have to subtract 4 from it.

In this equation, we should first separate the number into hundreds and units.

So, 104 = 100 + 4

On subtracting 4 from this number, we get

100 + 4 − 4

= 100

However, if you have to subtract 50 from 104, you can break it down as

104 = 50 + 50 + 4

On subtracting 50 from this number, we get

50 + 50 + 4 − 50

= 54

Partitioning of Shapes

Partitioning also refers to dividing shapes or sets into equal or unequal parts.

Let’s talk about shapes first.

A diameter or a line that passes through the center of a circle divides it into two equal parts. Look at the illustration given below:

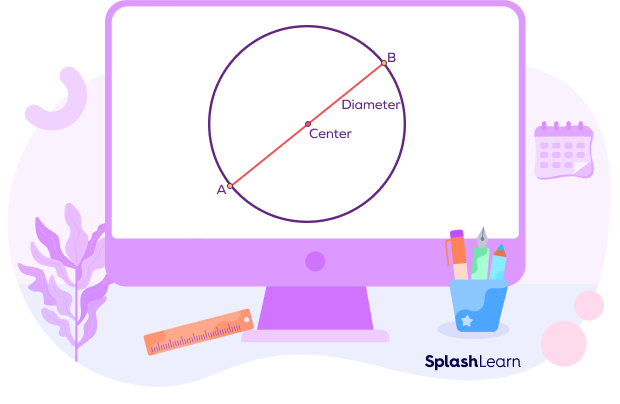
As you can see here, the circle is divided into two equal parts by line AB. You can represent each part as 1/2 or 

The area of each half = 1/2 x area of the circle.

Now, let’s consider a rectangle and partition it into three equal parts.

As seen here, you can represent each part as 1/3 or

The area of each equal part = 1/3 x area of the rectangle

Similarly, if you partition a square into four equal parts, you get an illustration like this:

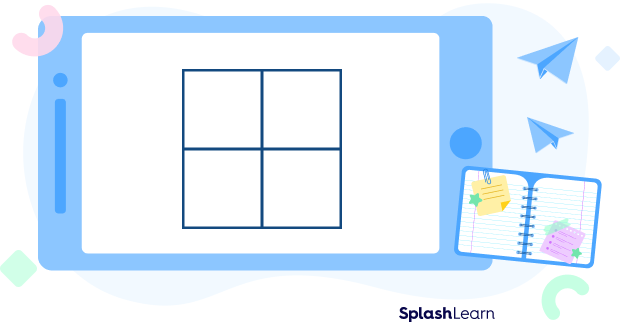
Here the area of each part = 1/4 x the area of the square.

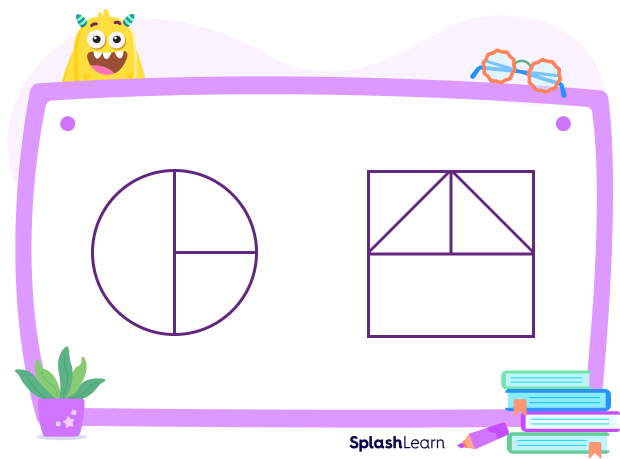
You can also divide a shape into unequal parts. You can consider the below examples to understand this. Here, each part is not partitioned equally.

Solved Examples

Example 1. Add the numbers 566 and 768 using the partitioning method.

Solution: Let’s first partition 566

566 = 500 + 60 + 6

Similarly,

768 = 700 + 60 + 8

So, 566 + 768

= 500 + 60 + 6 + 700 + 60 + 8

= 500 + 700 + 60 + 60 + 8 + 6 

= 1200 + 120 + 14

= 1200 + 134

= 1334

Example 2. Subtract 85 from 420 using the partition method.

Solution: Let’s first partition the numbers into hundreds, tens, and units.

420 − 85

= 400 + 20 − ( 80 + 5)

= 400 + 20 − 80 − 5

= 400 − 60 − 5

= 400 − 65

= 335

Example 3. Calculate the area of each part of a circle divided into two parts by a diameter. The area of the circle is 20 sq. cm.

Solution: We know that a diameter divides a circle into two equal parts.

Thus, the area of each half = 1/2 x the area of the circle

Area of circle = 20 sq. cm.

Area of each half = 1/2 x 20

= 10 sq. cm

Practice Problems

Frequently Asked Questions