What are Venn Diagram?
Venn diagrams are diagrams used to visually depict sets, relationships between sets, and operations on sets. The Venn diagram shows the relationship among sets using circles and the area they cover concerning each other.
A Venn diagram, also known as a set diagram, depicts several set operations like set intersection, set union, and set difference. We may also use it to represent subsets of a set.
History
English mathematician John Venn developed the Venn diagram in 1881. He created it to show inclusion and exclusion interactions between sets properly. However, he didn’t name it the Venn Diagram. He referred to the circles as ‘Eulerian circles.’ In his 1918 book, A Survey of Symbolic Logic, Clarence Lewis first called it the Venn diagram.
Parts of a Venn Diagram
- Universal Set
A Venn diagram includes a universal set and all other sets included in this universal set. A well-defined collection of objects is known as a set. The universal set (U) is typically depicted by a closed rectangle that contains all of the sets. Circles or ovals represent the sets and subsets.
In the above Venn diagram, the universal set includes all the elements in the rectangle. So, U = {2, 3, 4, 5, 6, 7, 8, 9}
- Subset
A subset is a set that is included within a larger set. The symbol ⊂ represents that a set is a subset of another set.
The above Venn diagram shows a universal set U, with sets A and B. The subset C has two elements: C = {4, 5}. This is again a part of A = {3, 4, 5}. All the elements of set C are a part of set A. So, set C is a subset of set A or C ⊂ A.
Set Operations Using Venn Diagrams
- Union of Sets
Suppose we have two sets, P and Q, with some elements in both of them. Then, the union of these sets will combine all the elements present in both sets. We represent this operation as P ∪ Q. The symbol ∪ represents the union of sets.
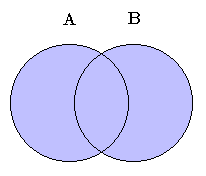
In the above Venn diagram, the purple shaded region represents the union A ∪ B of sets A and B.
- Intersection of Sets
Suppose we have two sets, P and Q. Then, the intersection of these sets will contain all the common elements in both sets. We represent this operation as P ∩ Q. The symbol ∩ represents the intersection of sets.
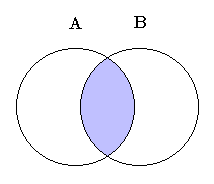
In the above Venn diagram, the purple-shaded portion represents the intersection of sets A and B.
- Complement of a Set
The region in the universal set, apart from the area covered by the set P, is the complement of set P. Complement of a set P (for example) is denoted by the symbol P’.
The complement of a set P’ denotes items that are not included in set P. The yellow-shaded region in the above Venn diagram denotes the complement P’ of the set P.
How to Draw a Venn Diagram
Venn diagrams may be created with a number of circles or any other closed figure. Because more than three circles in a Venn diagram get complex, we will generally include only two or three circles. Here are the four simple steps for drawing a Venn diagram:
Step 1: Sort all of the elements into sets.
Step 2: Make a rectangle and name it according to the relationship between the sets. This represents the universal set.
Step 3: Draw as many circles as the variety of groups or sets.
Step 4: Arrange all elements in the appropriate circles or sets.
For example, consider drawing a Venn diagram to sort vegetables according to their color. The vegetables are carrot, spinach, tomato, broccoli, cabbage, and beetroot.
Step 1: First, we sort the vegetables as per their color. So, carrot, tomato, and beetroot are red, while spinach, broccoli, and cabbage are green.
Step 2: We draw a rectangle to represent the universal set. Here, the theme – or universal set – is vegetables.
Step 3: We have two groups of vegetables. One group, R, includes red vegetables, and the other group, G, includes green vegetables.
Step 4: Arrange all the vegetables in their respective set.
Solved Examples
Q1. In a class of 30 students, 10 study English. Find the number of students in the class that do not study English using a Venn diagram.
- In the given Venn diagram,
Students studying English = 10
Students in the class = 30
So, from the above Venn diagram, the complement of the set E gives the number of students that do not study English.
Thus, E’ or the number of students who do not study English is 20.
Q2. Depict this information through a Venn diagram: there are 7 bottles of apple juice, 3 bottles of carrot juice, and 2 bottles of mixed fruit juice with both the juices.
- By using the given information, we can draw the Venn diagram as follows:
Q3. Find the union of sets P and Q, where P = {2, 4, 6} and Q = {1, 3, 5}
- The union of set P and Q includes all the elements of sets P and Q.
So, P ∪ Q = {1, 2, 3, 4, 5, 6}
Practice Problems
Venn Diagram
How can we represent the union of two sets A and B?
Option a. is the correct answer. A ∪ B represents the union of sets A and B.
How can we represent the intersection of two sets P and Q?
Option b. is the correct answer. P ∩ Q represents the intersection of sets P and Q.
How can we represent the complement of a set M?
Option c. is the correct answer. M’ represents the complement of set M.
Frequently Asked Question
How to draw a Venn diagram?
We can draw a Venn diagram by simply drawing a rectangle to represent the universal set. Then, draw circles in the rectangle to depict sets included in the universal set.
Can we use another shape apart from circles to represent sets?
Yes, we can use any shape to represent sets. Using a circular shape is not necessary.
What is the use of studying Venn diagrams?
Venn diagrams are used to improve the logic and reasoning abilities of young children. They are also used in areas where we need to categorize or group items and compare and contrast different things.
Do all Venn diagrams have overlapping circles?
Venn diagrams are typically represented through a rectangle and overlapping circles. But, it is not necessary that every Venn diagram has overlapping circles. If there is no intersection of sets, the circles in the Venn diagram do not overlap.
















