What Is an Onto Function?
Onto function is also known as a surjective function. For an onto function, each element in the second set (co-domain) has a preimage.
When we define a function from set X to set Y, the set X containing input values is called the domain of the function. The set Y of possible output values is called the co-domain. The subset of the co-domain containing the actual outputs is called the range of the function.
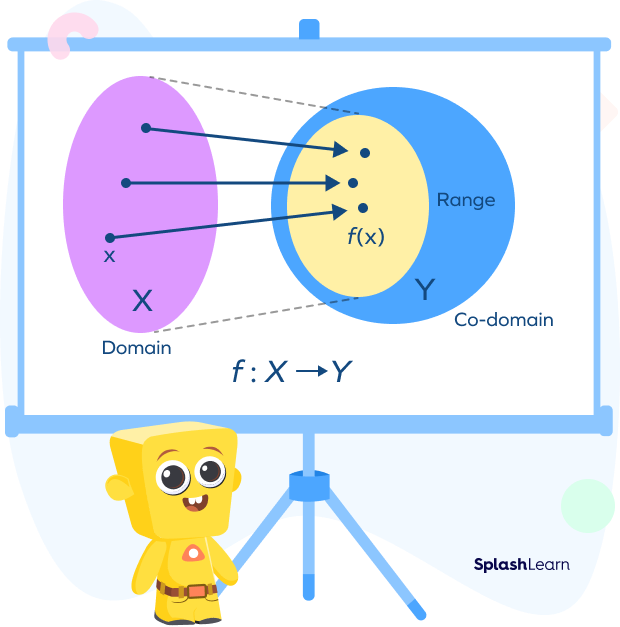
In case of onto functions, we have range = co-domain. It means that all the elements of the co-domain represent the range.
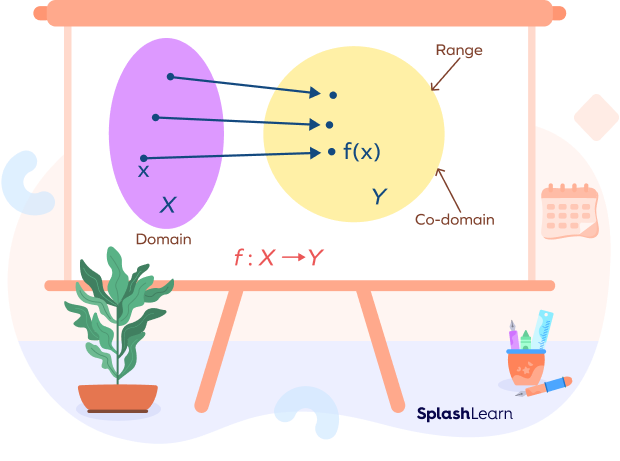
So, if a single element in Y is not mapped to an element of X, the function is not onto.
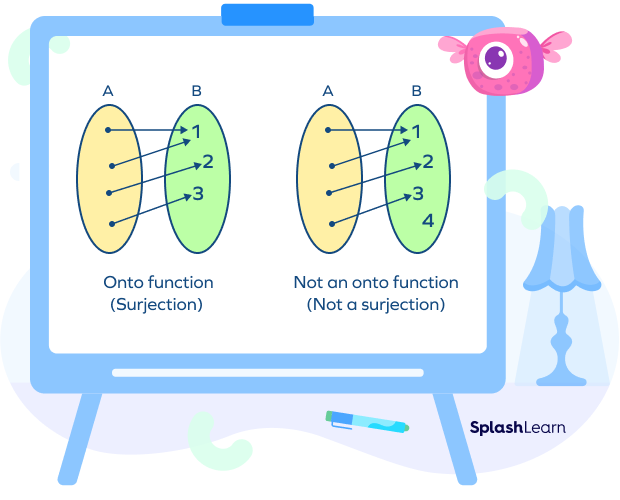
Onto Function Definition
A function f : A → B is called an onto function if each element of B is mapped to at least one element of A. For every b ∈ B, there is a ∈ A such that f(a) = b.
How to Prove a Function is Onto
To show that a function f is an onto function, put y = f(x), and show that we can express x in terms of y for any y ∈ B.
Example 1: f:R → R defined as f(x) = 2x
y = 2x
x $= \frac{y}{2}$
Thus, for every y R, we have $x = \frac{y}{2} ∈ R such that f(x) = y.
Thus, f is onto.
Example 2: Consider the function f:R → R defined as $f(x) = x^{2}$.
$y = x^{2}$
$x = \pm \sqrt{y}$
The square of any real number is non-negative.
It means that $y \ge 0$.
Thus, for $y \le 0$, we cannot find an element x such that f(x) = y.
Thus, the range of f(x) is the set of non-negative real numbers and the negative real numbers are not in the image of f(x).
As a result, f(x) is not onto.
Note: If you restrict the co-domain to ℝ+∪{0}, which is the set of non-negative real numbers, the function becomes onto.
Number of Onto Functions Formula
Consider a function f:A → B such that A has n elements and B has m elements.
| A | = n
| B | = m
Total number of onto functions = Total number of functions – Number of functions that are not onto
where
- Total number of onto functions $= m^{n}$
- Number of functions that are not onto =
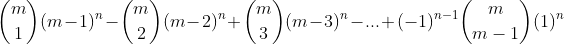
If n < m, the number of onto functions = 0
If n = m, the number of onto functions = m!
Properties of Onto Function
- The range of an onto function is equal to its co-domain.
- Each element in the codomain has at least one preimage. In other words, the function “hits” every element in the output set.
- Every onto function has a right inverse. Every function that has a right inverse is an onto function.
- Every onto function is not necessarily one-to-one.
- Compositions of onto functions are also onto. This means that if f: A → B and g: B → C are both onto, then g ◦ f: A → C is also onto.
Onto Function Graph
You can compare the range and co-domain using the graph and determine whether the function is onto or not. If the range equals codomain, the function is onto.
Thus, for onto functions, the graph must reach all the y-values in the codomain. If the graph does not hit all the y-values, it is not an onto function. The graph of an onto function will pass through every point in the range exactly once. It means that no element in the range is left out.
Facts about Onto Functions
- If a function is one-one and onto, it is called a bijective function.
- Every finite set with at least two elements can be matched one-to-one with a proper subset of itself.
- If a function’s range equals its codomain, it is onto.
Conclusion
In this article, we learned about onto functions, their properties, and also about how to identify onto functions with examples. Let’s recall and use these concepts to solve a few examples and MCQs!
Solved Examples on Onto Function
1. Show that the function f: R → R defined as $f(x) = x^{3}$is onto.
Solution:
To show that f is onto, we need to show that every y-value has a corresponding x-value such that f(x) =y.
Let y be any real number. Then we can solve for x by taking the cube root of both sides:
y $= x^{3}$
x $= y^{(1/3)}
Thus, for each y, there is $x = y^{(1/3)} such that f(x) = y.
Thus, f is onto.
2. Determine whether the function f: R → R defines as f(x) = 2x – 1 is onto.
Solution:
Let f(x) = y = 2x – 1
2x = y + 1
x $= \frac{(y + 1)}{2}$
For every y, we have $x =\frac{(y + 1)}{2}$, such that f(x) = y.
Thus, f is onto.
3. Let g: R → [0, ∞) be defined as g(x) = x². Is g an onto function?
Solution:
g(x) = x²
y = x²
x = $\sqrt{y}$
Every non-negative real number has a square root.
For every y in [0, ∞), we have x=y such that g(x) = y.
Yes, g is an onto function since every non-negative real number has a preimage in R.
4. Let f: R → R be a function defined by f(x) = 3x + 1. Is f onto?
Solution:
For f(x) = 3x + 1, let y be an element in the range of f.
Then, we need to find x such that f(x) = y.
y = 3x + 1
3x = y – 1
x $= \frac{y\;-\;1}{3}$
Every y in R has a preimage $x = \frac{y\;-\;1}{3}$ in R.
Thus, function is onto.
Practice Problems on Onto Function
Onto Function: Definition with Examples
A function is onto if
If range = codomain, the function is onto.
Onto function is also known as a
Onto function is also known as surjective function.
For an onto function f:$A\rightarrow B$, every b B has a A such that
For an onto function f:$A\rightarrow B$, every b B has a A such that f(a) = b.
Let f: $R \rightarrow R$. Which of the following will be an onto function?
f(x) =x is an identity function. Every element is mapped to itself. So, every element has a preimage. Thus, it is an onto function.
Consider f(x) =c defined on R. It will be an onto function if the range and the codomain are equal to ______
The range has only one element, c. Thus, if range = codomain = {c}, then the function will be onto.
Frequently Asked Questions about the Onto Function
What is the difference between an onto function and a one-one function?
A one-one function maps each element in the domain to a unique element in the codomain. Thus, every element of the range corresponds to exactly one element of its domain. The output values are never repeated.
Onto function maps every element in the codomain to at least one element in the domain. The function covers or hits each element in the codomain, thereby range = codomain.
Can a function be both one-to-one and onto?
Yes, a function can be both one-to-one and onto. Such a function is called a bijection.
When is a function not onto?
If there is an element y in the co-domain for which there is no x value in the domain such that f(x) = y.
What is the right inverse of a function?
For a function f : A→B, the function g : B→A is a right inverse of f if f∘g = I. It is called a right inverse because the inverse function is written to the right of the original function.
What is onto vs. one-to-one function?
- An onto function, also known as a surjective function, maps elements from the domain to the entire codomain, ensuring each element in the codomain is covered.
- A one-to-one function, also called an injective function, assigns unique elements from the domain to distinct elements in the codomain, avoiding repetition.
















