What is a Set?
We commonly use the terms like ‘a complete set of novels’ or ‘a set of cutlery’ in day-to-day life. What do we mean by the term ‘set’ here? It simply defines a collection of objects or things of the same type. Sets in math are also defined in the similar context.
Recommended Games
Set Definition
In mathematics, a set is defined as a collection of distinct, well-defined objects forming a group. There can be any number of items, be it a collection of whole numbers, months of a year, types of birds, and so on. Each item in the set is known as an element of the set. We use curly brackets while writing a set.
Consider an example of a set.
$\text{A} = \left\{1, 3, 5, 7, 9\right\}$.
It has five elements. It is a set of odd numbers less from 1 to 10.
What do we mean by ‘well-defined’ objects?
Consider an example. A collection of odd natural numbers less than 20 is defined, but a collection of brave students in a class is not defined.
We can represent a collection of odd natural numbers less than 20 in the form of a set as
$\text{B} = \left\{1, 3, 5, 7, 9, 11, 13, 15, 17, 19\right\}$.
The number of elements in the set are denoted by n(A) where A is a set.
Example: $\text{A} = \left\{1, 4, 9, 16, 25, 36, 49, 64, 81, 100\right\}$.
$n(A) = 10$.
The other word used for the number of elements in the set is called its cardinality.
Recommended Worksheets
Elements of a Set
Elements or members are the terms or items present in a set. They are enclosed in curly brackets and separated by commas. To represent that an element is contained in a set, we use the symbol “$\in$.” It is read as ‘belongs to.’
Suppose we have a set of even natural numbers less than 10.
$\text{A} = \left\{2, 4, 6, 8\right\}$ .
Here, $2 \in A$ but $3 \notin A$.
Representation of Sets
We represent the sets in different ways. The only difference is in the way in which the elements are listed. The different forms of representing sets are discussed below.
Roster Form
The most familiar and easy form used to represent sets is the roster form, in which the elements are enclosed in curly brackets and are separated by commas such as $\text{B} = \left\{1, 4, 9, 16, 25\right\}$, which is the collection of the square of consecutive numbers less than 30. The order of the elements does not matter and there can be an infinite number of elements in a set, which we define using a series of dots at the end of the last element. There are two types of sets in Roster Form:
Finite Roster Notation of Sets in which there are elements that can be counted, such as $\text{A} = \left\{5, 10, 15, 20, 25\right\}$ (The multiples of 5 less than 30.)
Infinite Roster Notation of Sets in which the elements can not be counted, such as $\text{B} = \left\{4, 8, 12, 16 …\right\}$ (The multiples of 4)
Set Builder Form
The set builder notation has a particular rule that describes the common feature of all the elements of a set. It uses a vertical bar in its representation along with a text describing the character of the elements, such as $\text{A} = \left\{ \text{x}\; |\; \text{x} \; \text{is a prime number}, x \le 20\right\}$. According to the statement, all the elements of the set are prime numbers less than or equal to 20. We use “:” place of the “|” sometimes.
Types of Sets
Let’s discuss different types of sets.
Singleton Sets
When a set has only one element, it is known as a singleton set.
Set $\text{A} = \left\{ \text{x}\; |\; \text{x}\; \text{is a whole number between}\;12\; \text{and}\;14\right\} = \left\{13\right\}$.
Null or Empty Sets
When a set does not contain any element, it is known as a null or an empty set. It is denoted by the symbol “$\Phi$” and it is read as “phi.”
Set $\text{B} = =$ Integers between 1 and $2 = \Phi$
Equal Sets
Two sets are said to be equal if they have the same elements in them. Suppose there are two sets $\text{A} = \left\{1, 4, 5\right\}$ and $\text{B} = \left\{1, 4, 5\right\}$. Here, $\text{A} = \text{B}$ because each element is the same.
Unequal Sets
Two sets are said to be unequal if they have at least one different element. Suppose we have two sets $\text{A} = \left\{1, 2, 5\right\}$ and $\text{B} = \left\{1, 2, 4\right\}$. Here, $\text{A} \neq \text{B}$ as $5 \in \text{A}$ but $5 \notin \text{B}$.
Equivalent Sets
Equivalent sets are the two sets that have the same number of elements, even if the elements are different. Suppose we have two sets $\text{A} = \left\{10, 11, 12, 13\right\}$ and $\text{B} = \left\{January, February, March, April\right\}$. Since $n(A) = n(B)$, A and B are equivalent sets.
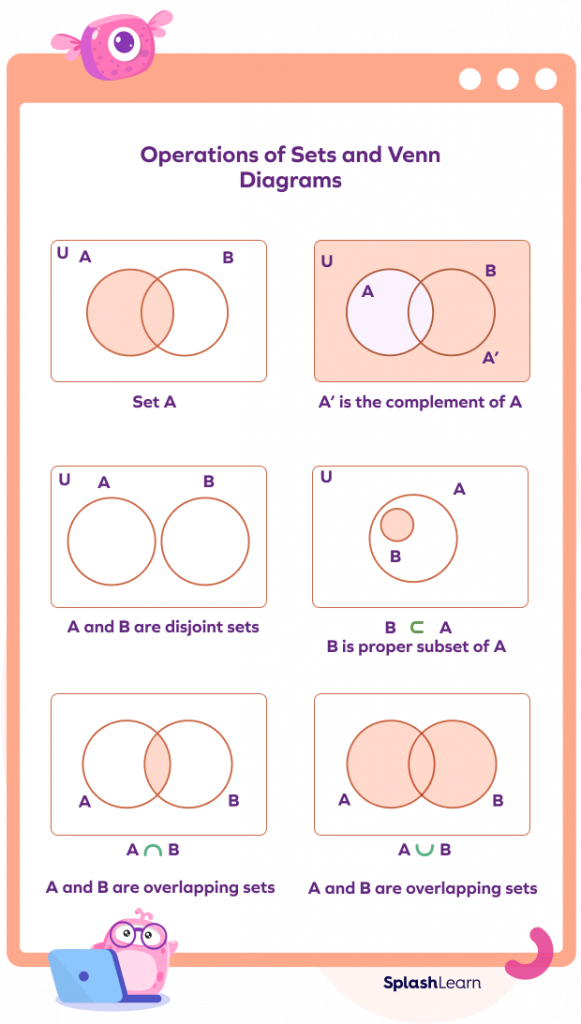
Overlapping Sets
If at least one element from set A is present in set B, then the sets are said to be overlapping. Example: $\text{A} = \left\{2, 3, 6\right\} \text{B} = \left\{6, 8, 12\right\}$. 6 is present in set A and set B. So, A and B are overlapping sets.
Subset and Superset
If every element in set A is also present in set B, then set A is known as the subset of set B, which is denoted by $\text{A} \subseteq \text{B}$ and B is known as the superset of set A, which is denoted by $\text{B} \supseteq \text{A}$.
Example: $\text{A} = \left\{1, 4, 7, 10, 12\right\}\; \text{B} = \left\{1, 4, 6, 7, 8, 10, 11, 12, 13\right\}$
$\text{A} \subseteq \text{B}$, since all the elements of A are present in B.
Also, set B is the superset of set A.
Universal Set
The collection of all the elements in regard to a particular subject is known as a universal set which is denoted by the letter “U.” Suppose we have a set U as the set of all the natural numbers. So, the set of even numbers, set of odd numbers, set of prime numbers is a subset of the universal set.
Disjoint Sets
Two sets are known as disjoint sets if they have no common elements in both sets. Consider two sets – $\text{A} = \left\{5, 6, 7\right\}$ and $\text{B} = \left\{2, 3, 4\right\}$. Here, set A and set B are disjoint sets as they have no elements in common.
Power Sets
The set of all subsets that a set could contain is known as the power set. Suppose we have a set $\text{A} = \left\{2, 3\right\}$. Power set of A is $= \left\{\left\{\varnothing\right\}, \left\{2\right\}, \left\{3\right\}, \left\{2,3\right\}\right\}$.
If n is the number of elements in a set, then the number of subsets $=2^{n}$.
Visual Representation of Sets Using Venn Diagram
The pictorial representation of sets represented as circles is known as the Venn diagram. The elements of the sets are inside the circles. The rectangle that encloses the circles represents the universal set. The Venn diagram represents how the sets are related to each other.

Operations on Sets
There are some operations on sets given below:
Union of Sets
B. Suppose we have two sets $\text{A} = \left\{1, 2, 3\right\}$ and $\text{B} = \left\{3, 4, 5\right\}$
$\text{A}\; \text{U}\; \text{B} = \left\{1, 2, 3, 4, 5\right\}$
Intersection of Sets
The intersection of sets is denoted by $\text{A} \cap \text{B}$ has the elements which are common in both set A and set B. Suppose we have two sets $\text{A} = \left\{1, 3\right\}$ and $\text{B} = \left\{3, 4\right\}$
$\text{A} \cap \text{B} = {3}$
Difference of Sets
We denote the set difference by $\text{A} – \text{B}$, which has the elements in set A that are not present in set B. Suppose we have two sets, i.e., $\text{A} = \left\{3, 4, 5\right\}$ and $\text{B} = \left\{5, 6, 7\right\}$
$\text{A} \;–\; \text{B} = \left\{3, 4\right\}$
Complement of a Set
The complement of a set A is denoted by A’, which is the set of all elements in the universal set that are not present in set A. A’ can also be represented as $\text{U} \;–\; \text{A}$, i.e., the difference in the elements of the universal set and set A.
Suppose $\text{U} =$ Set of Natural Numbers and $\text{A} =$ Set of Prime Numbers
So, $\text{U} \;–\; \text{A} =$ Set of all Non-prime Numbers.
Sets Formulas
There are some set formulas that we can use to find the number of elements.
For sets A and B,
- $n(A\; U\; B) = n(A) + n(B) – n(A \cap B)$
- $n(A − B) = n(A U B) − n(B)$
- $n(A − B) = n(A) − n(A \cap B)$
Properties of Sets
Here are the properties of sets:
| Set Property | Representation |
|---|---|
| Commutative Property | A ∪ B = B ∪ A A ⋂ B = B ⋂ A |
| Associative Property | A ∪ (B ∪ C) = (A ∪ B) ∪ C A ⋂ (B ⋂ C) = (A ⋂ B) ⋂ C |
| Distributive Property | A ∪ (B ⋂ C) = (A ∪ B) ⋂ (A ∪ C) A ⋂ (B ∪ C) = (A ⋂ B) ∪ (A ⋂ C) |
| Identity Property | A ∪ ∅ = A A ⋂ U = A |
| Complement Property | A ∪ A’ = U |
| Idempotent Property | A ∪ A = A A ⋂ A = A |
| Properties of ∅ and U | A ∪ ∅ = A A ⋂ ∅ = ∅ |
| A ∪ U = U A ⋂ U = A |
Solved Examples
1. How many elements are there in the set $\text{A} = \left\{ \text{x}\; : \text{x}\; \text{is a perfect square less than 30}\right\}$ ?
Solution: $\text{A} = \left\{1, 4, 9, 16, 25\right\}$
$n(A) = 5$
2. Arrange the set $A = \left\{ y : y^{2} = 36 ; y\; \text{is an integer}\right\}$ in roster form.
Solution: $y^{2} = 36 \Rightarrow y^{2} − 36 = 0 \Rightarrow y = \pm 6$
$\text{A} = { –\; 6, 6}$
3. Write the set $\text{B} = \left\{1, 2, 5, 10, 17\right\}$ in set builder form.
Solution: $0^{2} + 1 = 1$
$1^{2} + 1 = 2$
$2^{2} + 1 = 5$
$3^{2} + 1 = 10$
$4^{2} + 1 = 17$
So, in roaster form $\text{B} = \left\{y : y^{2} + 1, y \lt 5\right\}$
4. If A is a set of prime numbers and B is a set of even numbers. What will be $\text{A} \cap \text{B}$?
Solution: Only 2 is the number, which is a prime number as well as an even number. So, $\text{A} \cap \text{B} = {2}$.
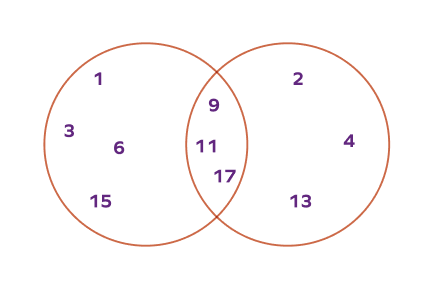
5. Draw a Venn diagram for the sets $\text{A} = \left\{1, 3, 6, 9, 11, 15, 17\right\}$ and $\text{B} = \left\{2, 4, 9, 11, 13, 17\right\}$.
Solution:
Practice Problems
What is a Set in Math
Which of the following sets denotes $\left\{\right\}$?
There is no element in $\left\{\right\}$. So, it is a null set.
If $\text{A} = \left\{\;–\; 1, 0, 2, 3, 5, 7\right\}$ and $\text{B} = \left\{0, 1, 2, 3, 5, 6\right\}$, then what is $\text{A}\; \text{U}\; \text{B}$?
$\text{A}\; \text{U}\; \text{B} = \left\{\; –\; 1, 0, 1, 2, 3, 5, 6, 7\right\}$
If $\text{P} = \left\{ \;–\; 10, \;–\; 7, \;–\; 4, \;–\; 3, \;–\; 2, \;–\; 1\right\}$ and $\text{Q} = \left\{ \;–\; 9, \;–\; 8, \;–\; 7, \;–\; 6, \;–\; 4, \;–\; 2\right\}$ then __ denotes $\left\{ \;–\; 10, \;–\; 3, \;–\; 1\right\}$
The elements in $\left\{ \;–\; 10, \;–\; 3, \;–\; 1\right\}$ are elements that are in Set P but not in Set Q.
How many subsets will be there if $n(A) = 3$ where A is a set?
Number of subsets $= 2^{n} = 2^{3} = 8$
If $n(A)$ = $16,n (B) = 18$ and $n(A \cup B) = 7$, then what is the value of $n(A \cup B)$?
$n(A \cup B) = n(A) + n(B) \;-\; n(AB) = 16 + 18 \;-\; 7 = 27$
Frequently Asked Questions
What are sets formula if sets are disjoint?
For disjoint sets A and B;
- $n(A U B) = n(A) + n(B)$
- $A \cap B = \varnothing$
- $n(A − B) = n(A)$
Is {0} a null set ?
No. There is one element inside the brackets. So, it is a singleton set, not a null set.
What is a Cartesian Product in sets?
Cartesian Product of Set A and B is defined as an ordered pair $(x, y)$ where $x \in A$ and $y \in B$.
How is set theory applicable in daily lives?
In real life, sets are used in bookshelves while arranging the books according to alphabetic order or genre; closets where dresses, tops, jeans are kept as a set, etc.
Does the union of two sets include the intersection of the sets?
Yes, the union of two sets includes the intersection of the sets. Union of set A and B includes the elements either in set A or in set B or in both set A and B.



















