Surface Area of a Cube

Surface Area of a Cube: Introduction

Have you ever played the Rubik’s cube or a dice? What is the shape of a dice? Both these objects have the shape of a cube.

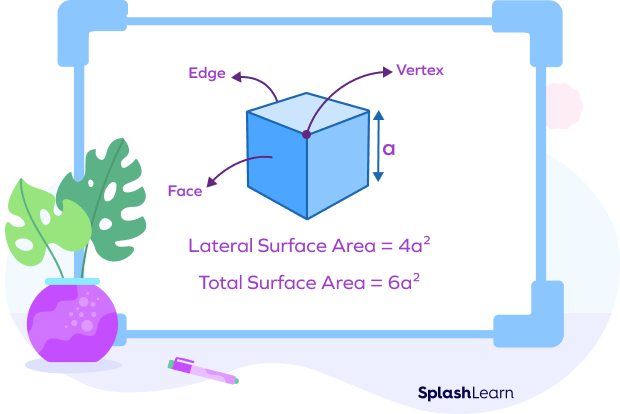
A cube is a three-dimensional solid having 6 congruent square faces. So, all its edges are equal in size. If you calculate the sum of the areas of all its 6 faces, it gives us the surface area of the cube.

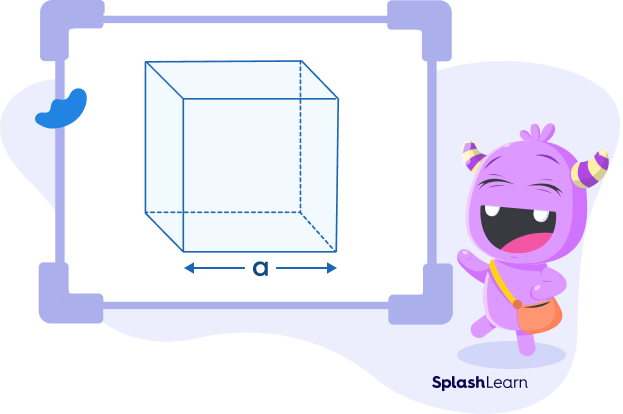
The surface area of a three-dimensional shape is the sum of the areas of all the faces of the shape. If you wish to calculate the amount of color paint required to paint the surface of the cube, you will need to know the surface area of the cube!

What Is the Surface Area of a Cube?

Surface area of a cube is the total area of the outer surface of the cube.

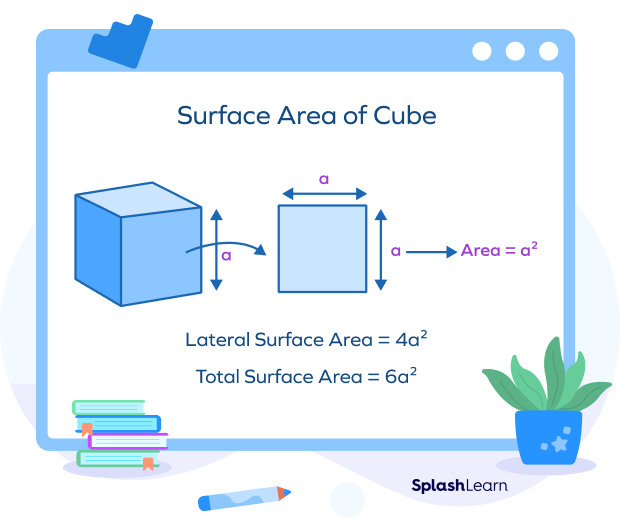
Since the cube has 6 congruent square-shaped faces, we can find the total surface area of the cube as $6a^{2}$, where a is the length of the side of the cube.

There are two types of surface areas in a cube.

• Lateral surface area: Total area of the lateral faces of the cube
• Total surface area: Total area of all the faces of the cube

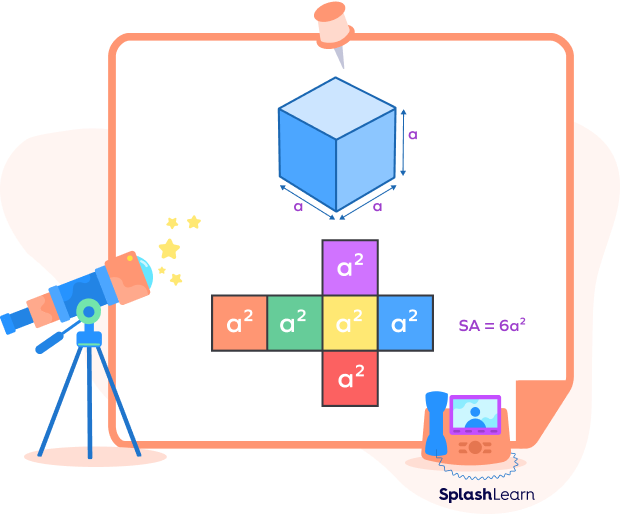
In other words, the surface area of a cube is the number of unit squares needed to cover the outer surfaces of the solid.

Surface Area of a Cube Definition

The total surface area of a cube is the sum of all the areas of the faces of the cube.

It is the number of unit squares needed to cover the outer surfaces of the solid. Surface area, just like any other area, is also measured in unit squares. 

If the side of the cube is given by “a” unit, then the total surface area is given by $6a^{2}$. 

The lateral surface area is the sum of the area of the lateral faces or side faces of the cube. The lateral surface area of the cube is $4a^{2}$.

Total Surface Area of Cube

The total surface area of a cube implies the total area covered by all six faces of a cube.

The formula to calculate the TSA of a cube, we find the sum of the areas of these 6 faces.

The area of each face with length measuring “a” units $= a^{2}$

Now, we know that there are 6 faces of a cube.

Total surface area of a cube formula $= 6a^{2}$

Lateral Surface Area of Cube

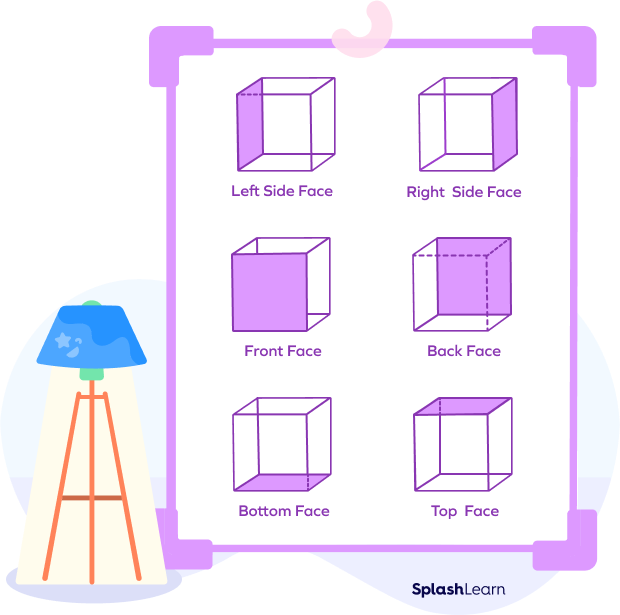
The lateral surface area of a cube implies the total area covered by the side or lateral faces of a cube. In lateral surface area, we include only the sides but not the top and bottom of the cube.

The formula to calculate LSA, we find the sum of areas of these 4 faces.

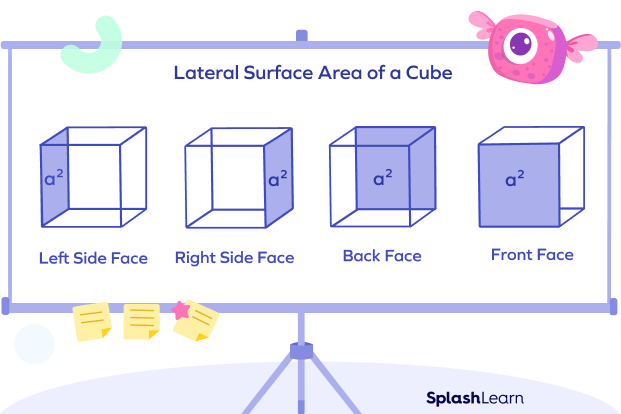
The area of each face with length measuring “a” units $= a^{2}$

Now, we know that there are 6 faces of a cube but the top and bottom are excluded in the lateral surface area.  

Lateral surface area of a cube $= 4a^{2}$

Surface Area of Cube Formula

If the side of the cube is given by “a” unit, then 

Total surface area of a cube $= 6a^{2}$

Lateral Surface area of a cube $= 4a^{2}$

How to Calculate the Surface Area of a Cube?

To find the surface area of a cube, the steps are mentioned below:

Step 1:  Identifying the length of the side of the cube.

Step 2: Finding the square of the length of the side of the cube. Such that we have an area of a single flat surface.

Step 3: IF we wish to find out the total surface area, we calculate the product of the square of side length by 6, or by using the formula $6a^{2}$.

Whereas if we wish to find the lateral surface area, we multiply the product of the square of side length by 4 or  by using the formula $4a^{2}$.

Total Surface Area of Cube Formula

Total surface area of a cube $6a^{2}$

Example: Jason wishes to wrap a gift with cloth. The gift is square in shape. The length of each side wall is 5 inches. How to find surface area of a cube shaped gift that he has to cover.

Solution:

We know that total Surface area of a cube $6a^{2}$

Here, $a = 5$ inches.

Putting the values in the formula, 

Area that he has cover $= 6a^{2}$

 $= 6 \times (5 inches)^{2}$

$= 6 \times 25$ $inches^{2}$

$= 150$ $inches^{2}$

Hence,  the area that he has to cover $= 150$ $inches^{2}$

Lateral Surface Area of Cube Formula

Lateral Surface area of a cube $= 4a^{2}$

Example: Larry wishes to paint the walls of his room. The walls are square in shape. The length of each wall is 96 inches. Find the area that he has to cover.

Solution:

We know that Lateral Surface area of a cube $= 4a^{2}$

Here, $a = 96$ inches.

Putting the values in the formula, 

Area $=  4a^{2}$

 $= 4 \times (96 inches)^{2}$

$= 4 \times 9216$ $inches^{2}$

$= 36864$ $inches^{2}$

Hence,  the area that he has to cover $= 36864$ $inches^{2}$

How to Find the Length of Edge of the Cube?

Using the formula to find the surface area of a cube we can calculate the side of the cube.

It is just like using the above mentioned formula but in a reverse way.

Let the total Surface area of a cube be “A.”

We know that total Surface area of a cube $= 6a^{2}$

$\Rightarrow A =  6a^{2}$

$\Rightarrow a^{2} = \frac{A}{6}$

$\Rightarrow a = \sqrt{\frac{A}{6}}$

Here, “a” – length of side

“A” – total surface area of a cube

Fun Facts

• A cube has 6 faces, 12 edges, and 8 vertices.
• All the edges of a cube have the same length.

Conclusion

In this article, we learned about the surface area of a cube. We studied the total surface area of a cube and the lateral surface area of a cube. Let us now solve some practice problems to understand the concept better. 

Solved Examples

1. The length of the side of the cube is 20 in. Find the total surface area of the cube.

Solution:

Length of the side of the cube, $a = 20$ in.

Using the formula for the area of the cube, which is: $A = 6a^{2}$,

$A = 6 \times 20 \times  20$ $in^{2}$

$A = 2400$  $in^{2}$

Therefore, the surface area of the cube is 2400 square inches.

2. Kevin has been given a cube of base area 25 square units. Find the length of the side of the cube and the total surface area of the cube.

Solution:

The base area of the cube $= 25$ square units.

Length of the side of the cube’a’ $= \sqrt{25} = 5$ units.

Total surface area: $A = 6a^{2}$

$A = 6 \times 5 \times 5$

$A = 150$ $in^{2}$

Therefore, the length of the base of the cube is 5 units, and the area of the cube is 150 square units.

3. What is the lateral surface area of a cube of side length $=  60$ feet?

Solution:

Given, side length $(a) = 60$ feet.

Lateral surface area: $L = 4a^{2}$

$L = 4 \times 3600$ $ft^{2}$

$L = 14400$ $ft^{2}$

Therefore, the lateral surface area of the cube is 14400 square feet.

4. Calculate the cost required to paint a box which is in cube shape having an edge length of 2 feet. If the cost of painting an aquarium is $\$10/ft^{2}$.

Solution:

Total surface area of aquarium $= 6 \times a^{2}$

$= 6 \times (2$ $ft)^{2}$

$= 24$ sq. ft

Total cost of painting the aquarium $= 10  \times 24= \$240$

5. Find the length of the edge of the cube, if its area is 1200 sq. cm.

Solution:

Given, area $= 1200$ sq. cm.

We know,Length of edge of cube $= \sqrt{\frac{A}{6}} = \sqrt{\frac{1200}{6}} = \sqrt{200} = 14.14$ $cm$.

Practice Problems

Frequently Asked Questions