What Is the Exterior Angle Theorem?
Exterior angle theorem states that the measure of an exterior angle of a triangle is equal to the sum of two remote interior angles.
The remote interior angles or opposite interior angles are the angles that are non-adjacent with the exterior angle.
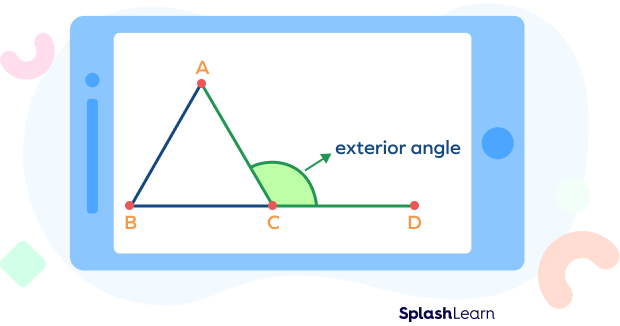
A triangle is a polygon with three sides. When we extend any side of a triangle, an angle is formed by the adjacent side and the extended ray. This angle is known as the “exterior angle” of a triangle.
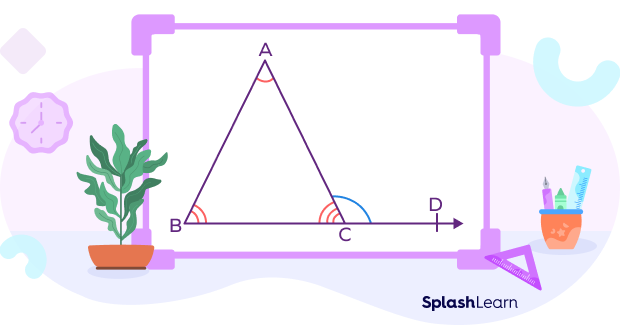
In the figure given below, the exterior angle $\angle ACD$ is formed by extending the side BC.
Recommended Games
Exterior Angle Theorem Statement
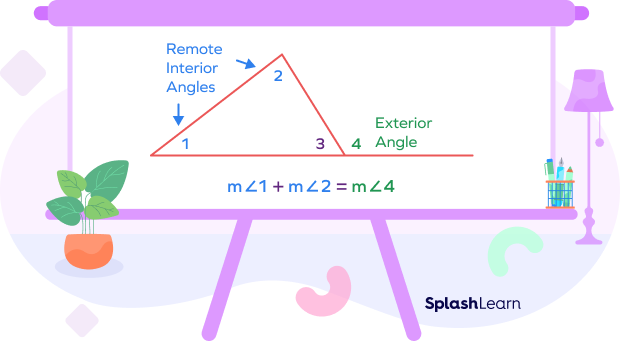
According to the exterior angle theorem, the measure of an exterior angle of a triangle is equal to the sum of the measures of the two opposite (remote) interior angles.
Take a look at the triangle shown in the figure given below.
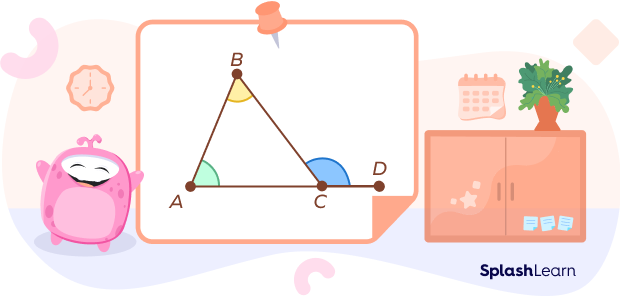
$\angle BCD$ is the exterior angle and its two opposite interior angles are $\angle A$ and $\angle B$.
According to the exterior angle theorem,
$\angle BCD = \angle A + \angle B$
We can use this theorem to find the measure of an unknown angle in a triangle.
Example: Find x.
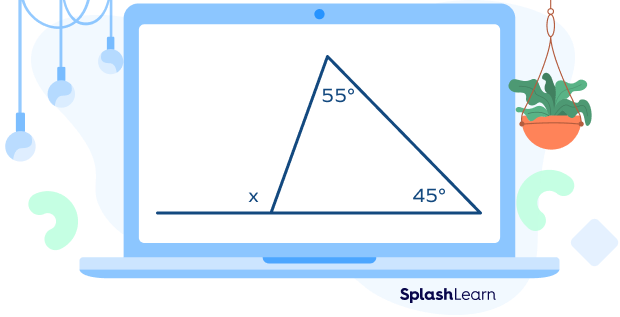
Here, x is the exterior angle with two opposite interior angles measuring $55^\circ$ and $45^\circ$.
By the exterior angle theorem,
$x = 55^\circ + 45^\circ = 100^\circ$
Recommended Worksheets
Proof of Exterior Angle Theorem
We can prove the exterior angle theorem using two methods.
Using Properties of Triangles
We can prove the exterior angle theorem with the known properties of a triangle.
Consider a $\Delta ABC$.
$\angle ACD$ is the exterior angle.
$\angle A + \angle B + \angle C = 180^\circ$ (Angle Sum Property of a triangle) …(1)
$\angle C = 180^\circ \;–\; (\angle A + \angle B)$ …(2)
$\angle ACD = 180^\circ \;–\; \angle C$ (Linear Pair of Angles) …(3)
Substituting the value of c in equation 3, we get
$\angle ACD = 180^\circ \;-\; \left[180^\circ \;-\; (\angle A + \angle B)\right]$
$\angle ACD = 180^\circ \;-\; 180^\circ + (\angle A + \angle B)$
$\angle ACD = \angle A + \angle B$
Hence proved.
Using Properties of Transversal and Parallel Lines
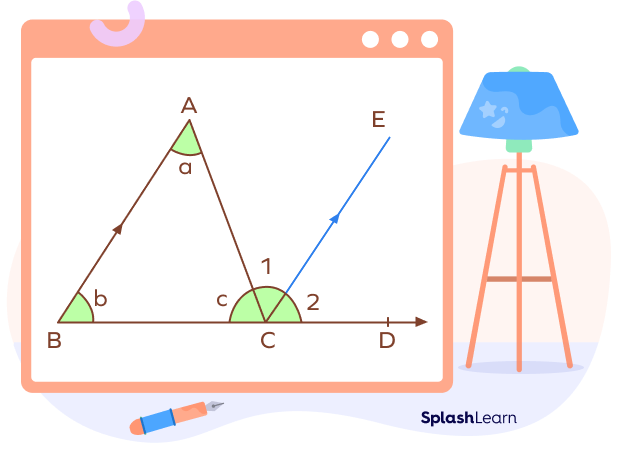
Given: Consider a $\Delta ABC$ where a,b and c are the three interior angles.
Construction: Extend the side BC. Let D be any point on the extended side BC. Now an exterior angle, $\angle ACD$ is formed. Draw a line CE parallel to AB.
Angles 1 and 2 are the angles formed by the line CE such that
$\angle ACD= \angle 1 + \angle 2$
Proof:
$AB || CE$
AC is the transversal.
So, $\angle a = \angle 1$ (Pair of alternate angles)
$AB || CE$.
BD is the transversal.
So, $\angle b = \angle 2$ (Pair of corresponding angles)
$\angle ACD = \angle 1 + \angle 2$ (Construction)
Substituting the value of $\angle 1$ and $\angle 2$, we get
$\angle ACD = \angle a + \angle b$
Hence, we proved that the exterior angle of a triangle is equal to the sum of the two opposite interior angles.
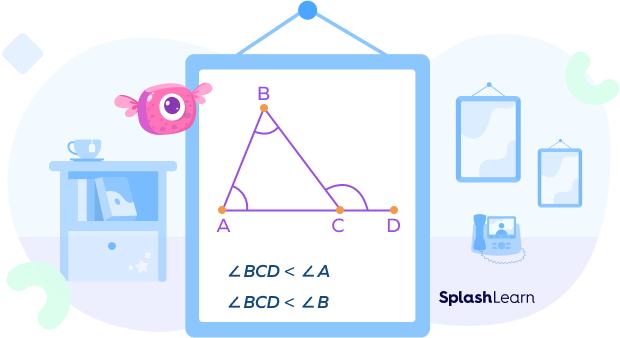
Exterior Angle Inequality Theorem
The exterior angle inequality theorem states that the measure of any exterior angle of a triangle is greater than each of the opposite interior angles.
This theorem holds true for all the six exterior angles of a triangle.
Conclusion
In this article, we learned about the exterior angle theorem, its statement and proof. We also learned the exterior angle inequality theorem. Let’s solve a few examples and practice problems based on these concepts.
Solved Examples on Exterior Angle Theorem
1. Find the value of $\angle ACB$ in the following figure.

Solution:
$\angle CAD$ is the exterior angle of $\Delta ABC$.
By the exterior angle theorem,
$\angle CAD = \angle ABC + \angle ACB$
$120^\circ = 40^\circ + \angle ACB$
$\angle ACB = 120^\circ \;-\; 40^\circ = 80^\circ$
2. Find the value of x in the following figure.
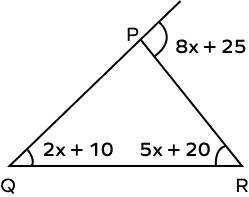
Solution:
$(8x + 25)^\circ$ is the exterior angle of $\Delta PQR$.
Its remote interior angles are $(2x + 10)^\circ$ and $(5x + 20)^\circ$.
By the exterior angle theorem,
$8x + 25 = 2x + 10 + 5x + 20$
$8x\;-\;2x\;-\;5x = 10 + 20\;-\;25$
$x=5$
3. Find the value of y in the following figure.
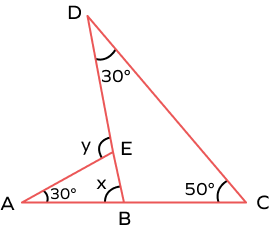
Solution:
There are two triangles in the figure, $\Delta DBC$ and $\Delta ABE$.
$\angle EBA = x$ is the exterior angle of $\Delta DBC$.
By the exterior angle theorem,
$\angle EBA = \angle BDC + \angle BCD$
$x = 30^\circ + 50^\circ = 80^\circ$
$x = 80^\circ$
$\angle DEA = y$ is the exterior angle of $\Delta ABE$.
By the exterior angle theorem,
$\angle DEA = \angle EBA + \angle BAE$
$y = x + 30^\circ$
$y = 80^\circ + 30^\circ$
$y = 110^\circ$
4. Find the value of $\angle PRQ$ using exterior angle theorem.
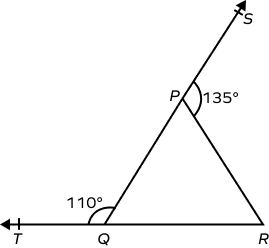
Solution:
QS is a straight line.
$\angle SPR + \angle QPR = 180^\circ$ (Angles in a linear pair.)
$135^\circ + \angle QPR = 180^\circ$
$\angle QPR = 180^\circ \;-\; 135^\circ = 45^\circ$
$\angle TQP$ is the exterior angle of $\Delta PQR$.
By the exterior angle theorem,
$\angle TQP = \angle PRQ + \angle QPR$
$110^\circ =\angle PRQ + 45^\circ$
$\angle PRQ = 65^\circ$
Practice Problems on Exterior Angle Theorem
Exterior Angle Theorem: Definition, Proof, Examples, Facts, FAQs
What will be the value of x in the following figure?
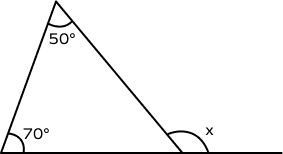
x is the exterior angle of the triangle.
By the exterior angle theorem,
$x = 50^\circ + 70^\circ = 120^\circ$
The exterior angle of a triangle equals the sum of __________.
An exterior angle of a triangle equals the sum of remote interior angles.
Find the value of x in the following figure.
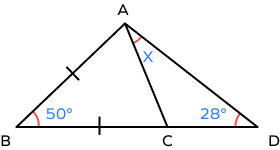
In $\Delta ABC,\; AB = BC\Rightarrow \angle BAC = \angle BCA = y$
By Angle Sum Property of a Triangle,
$y + y + 50^\circ = 180^\circ$
$2y = 130^\circ$
$y = 65^\circ$
$\angle ACB = y$ is the exterior angle of $\Delta ACD$.
$y = \angle CAD + \angle CDA$
$65 = x + 28^\circ$
$x = 37^\circ$
What will be the value of each exterior angle of an equilateral triangle?
Each interior angle of an equilateral triangle is $60^\circ$.
Exterior angle $= 60^\circ + 60^\circ = 120^\circ$
Frequently Asked Questions on Exterior Angle Theorem
Why is the sum of exterior angles of a triangle is $360^\circ$?
The sum of angles in a triangle is $180^\circ$. Each exterior angle of a triangle equals the sum of two remote interior angles. If we add the three exterior angles, we will have to add each interior angle twice. Thus, the sum of the measures of the exterior angles of a triangle is $360^\circ$ degrees.
What is the difference between angle sum property of a triangle and exterior angle property of a triangle?
According to the angle sum property of a triangle, the sum of all the interior angles of a triangle equals $180^\circ$. On the other hand, the exterior angle theorem states that exterior angle is equal to the sum of remote interior angles.
If each interior angle of a triangle gets doubled, then how will it affect the exterior angle of the triangle?
If each interior angle of a triangle gets doubled, then the exterior angle of the triangle gets doubled.
Original equation for the exterior angle “e”: $e = a + b$
New equation: $e = 2a + 2b = 2(a+b) = 2e$
How many exterior angles does a triangle have?
A triangle has 6 exterior angles.
What is the exterior angle theorem formula?
Exterior Angle $=$ The sum of two remote (opposite) interior angles





























