Compensation in Math – Definition With Examples

What Is Compensation in Math?

A compensation strategy helps to redefine and simplify an addition, subtraction, multiplication, or division problem. It also makes mental computation easier. 

Let’s consider an example. You have $\$36$, of which you spent $\$17$. How much money do you have left with you? You will need to subtract 17 from 36 to find out!

We know that $17 + 3 = 20$. So, subtracting 20 from 36 and then adding the extra 3 is easier than trying to subtract 17 mentally. We wanted to subtract 17, but we subtracted 20. So, the number 3 needs to be added again to balance the operation.

We can write this as: 

$36 \;-\; 17 = (36 \;-\; 20) + 3 = 16 + 3 = 19$

Example 2: Let’s consider another example.

Say we have to find $25 + 16$.

First, we round off the second number (16) to the nearest multiple of 10, which is 20.

$25 + (16 + 4) = 25 + 20$

$= 45$

Now, we compensate by subtracting 4 from 45 to get the answer.

$45 \;-\; 4 = 41$

Compensation in Math Definition 

Compensation can be defined as a method of adding or taking away numbers to make the calculation simple. Compensation in math often helps to reach a friendly number (such as a multiple of 10). 

Example: $6 + 9$

Let’s add 20 instead of 9. Why? Simply because adding 10 is easier than adding 9!

$6 + 10 = 16$

We added an extra 1. We have to compensate for that.

$16 \;-\; 1 = 15$

Thus, $6 + 9 = 15$

If you add some extra value, you have to subtract the same value to compensate. Similarly, if you subtract more than required, you have to add to make up for that.

How to Perform the Compensation Strategy?

Let’s understand different compensation strategies with examples.

Additive Compensation Method

This is the compensation addition strategy that makes addition of complex numbers easier. Let’s take a look at these examples.

Example 1: $56 + 35$

Step 1: Round off 56 to the nearest multiple of 10, which is 60.

$(56 + 4) + 35$

$= 60 + 35$

$= 95$

Step 2: Compensate by subtracting the extra 4 from the sum to reach the answer.

$95 \;-\; 4 =  91$

Example 2: $80 + 395$

Step 1: Round off the second number (395) to the nearest multiple of 10.

$80 + (395 + 5)$

$= 80 + 400$

$= 480$

Step 2: Compensate by subtracting the extra 5 from the sum to get the final answer.

$480 \;-\; 5 = 475$

Subtraction by Equal Addition Method

This compensation strategy is helpful in solving subtraction problems. Here are some examples.

Example 1: $67 – 59$

To simplify the subtraction, we add the same number to both numbers to make either one a multiple of 10.

$(67+1) \;-\; (59+1)$

$= 68 \;-\; 60$

$= 8$

Example 2: $83 \;-\; 26$

Again, we add the same number to both sides to make one of them a multiple of 10.

$(83 + 4)  – (26 + 4)$

$= 87  \;-\; 30$

$= 47$

Multiplicative Compensation Method

This compensation strategy makes complex numbers easier to multiply. Let’s look at these two compensation strategy examples to understand this better.

Example 1: $76 \times 5$

Let’s multiply 76 by 10 and compensate by dividing the answer by 2.

$76 \times 5 = 76 \times \frac{10}{2} = \frac{760}{2} = 380$

Example 2: $208 \times 25$

Let’s multiply 208 by 100 and compensate by dividing the answer by 4.

$208 \times 25 = 208 \times \frac{100}{4} = \frac{20800}{4} = 5200$

Division Compensation Method

This compensation strategy makes complex numbers easier to multiply. We can understand it with the help of the following examples.

Example 1: $96 \div 24$

To simplify the division, we divide both numbers by the same number.

Here, $\frac{96}{2} = 48$

$\frac{24}{2} = 12$

So, $\frac{96}{24} = \frac{48}{12}$

Now, for further division, we will need to know multiplication tables up to 12. 

Since $12 \times 4 = 48$,

$\frac{48}{12} = 4$  

Example 2: $245\div 5$

Instead of dividing by 5, we can multiply by 2 and then compensate by dividing the result by 10.

$\frac{245}{5} = \frac{245}{10} \times 2 = \frac{490}{10} = 49$

Here, $245 \times 2 = 490$

Now, we divide 490 by 10 to get the final answer.

$\frac{490}{10} = 49$.

What Is the Difference between Compensation and Transformation?

In a few math textbooks, you will find the term transformation used instead of compensation. Although a difference does exist between both the terms.

In transformation, both numbers are adjusted or changed simultaneously. On the other hand, in compensation, one number is adjusted or changed, and in the next step, the other number undergoes adjustment.

Let’s understand the difference better with the help of an example.

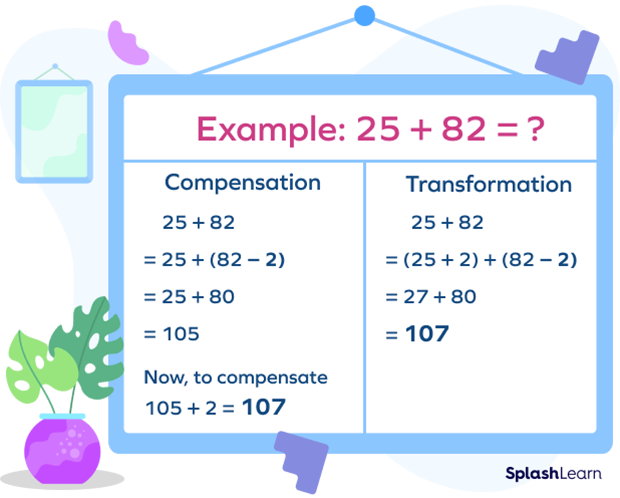
Conclusion

The compensation strategy in math refers to adding a number to one and subtracting it from the other later on to ensure that the balance remains the same.

Compensation in math makes it easy to solve complex addition, subtraction, multiplication, and division problems. Knowing compensation is also important because it enhances your brain’s ability to think creatively about solutions to problems. 

Solved Examples on Compensation in Math

Example 1: Calculate $\frac{260}{5}$.

Solution: 

Here, we can easily make the denominator 10. 

We will multiply 5 by 2.

Now, to compensate, we will also multiply the numerator (which is 260) by 2.

$\frac{260 \times 2}{5 \times 2} = \frac{520}{10} = 52$

Example 2: Find $304 + 49$.

Solution: First, we round off 49 to make it a multiple of 10.

$304 + (49 + 1)$

$= 304 + 50$

$= 354$

Now, we compensate by subtracting 1 from the sum to reach the final answer as

$354 \;-\; 1 = 353$

Example 3: Determine $365 \;-\; 177$.

Solution: We will subtract 180 from 365.

$365 \;-\; (177 + 3)$

$= 365 \;-\; 180$

$= 185$

Compensate by adding 3.

$365 \;-\; 177 = 185 + 3 = 188$

Example 4: Multiply 278 by 50.

Solution: Here, we divide 278 by 2 and compensate by multiplying 50 by 2 to make at least one number a multiple of 10.

$278 \div 2 = 139 \;-\;$ (i)

$50 \times 2 = 100 \;-\;$ (ii)

Now, we multiply both (i) and (ii) to get the final answer as

$139 \times 100 = 13,900$

Example 5: Divide 135 by 15.

Answer: Here, we divide both numbers by 3.

$135\div 3 = 45$

$15 \div3 = 5$

Since $5 \times 9 = 15$, upon dividing 45 by 5, we will get,

$45 \div5 = 9$

Practice Problems on Compensation in Math

Frequently Asked Questions on Compensation in Math