Experimental Probability

Experimental Probability: Introduction

In mathematics, probability refers to the chance of occurrence of a specific event. Probability can be measured on a scale from 0 to 1. The probability is 0 for an impossible event. The probability is 1 if the occurrence of the event is certain.

There are two approaches to study probability: experimental and theoretical. 

Suppose you and your friend toss a coin to decide who gets the first turn to ride a new bicycle. You choose “heads” and your friend chooses “tails.” 

Can you guess who will win? No! You have $\frac{1}{2}$ a chance of winning and so does your friend. This is theoretical since you are predicting the outcome based on what is expected to happen and not on the basis of outcomes of an experiment.

So, what is the experimental probability? Experimental probability is calculated by repeating an experiment and observing the outcomes. Let’s understand this a little better.

Experimental Probability: Definition

Experimental probability, or empirical probability, is the probability calculated by performing actual experiments and gathering or recording the necessary information. How would you define an experiment? The math definition of an experiment is “a process or procedure that can be repeated and that has a set of well-defined possible results or outcomes.”

Consider the same example. Suppose you flip the coin 50 times to see whether you get heads or tails, and you record the outcomes. Suppose you get heads 20 times and tails 30 times. Then the probability calculated using these outcomes is experimental probability. Here, the experimental meaning is connected with such experiments used to determine the probability of an event.

Now that you know the meaning of experimental probability, let’s understand its formula.

Experimental Probability Formula

Experimental Probability for an Event A can be calculated as follows:

P(E) $= \frac{Number of occurance of the event A}{Total number of trials}$

Let’s understand this with the help of the last example. 

A coin is flipped a total of 50 times. Heads appeared 20 times. Now, what is the experimental probability of getting heads?

Experimental probability of getting heads $= \frac{Number of occurrences}{Total number of trials}$

P (Heads) $= \frac{20}{50} = \frac{2}{5}$

P (Tails) $= \frac{30}{50} = \frac{3}{5}$

Experimental Probability vs. Theoretical Probability

Theoretical probability expresses what is expected. On the other hand, experimental probability explains how frequently an event occurred in an experiment.

If you roll a die, the theoretical probability of getting any particular number, say 3, is $\frac{1}{6}$. 

However, if you roll the die 100 times and record how many times 3 appears on top, say 65 times, then the experimental probability of getting 3 is $\frac{65}{100}$.

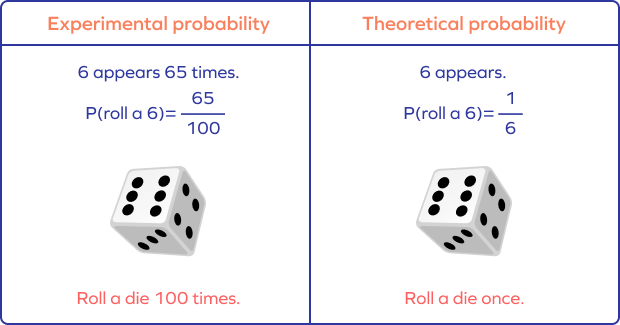
Theoretical probability for Event A can be calculated as follows:

P(A) $= \frac{Number of outcomes favorable to Event A}{Number of possible outcomes}$

In the example of flipping a coin, the theoretical probability of the occurrence of heads (or tails) on tossing a coin is

P(H) $= \frac{1}{2}$ and  P(T) $= \frac{1}{2}$ (since possible outcomes are $2 -$ head or tail)

Experimental Probability: Examples

Let’s take a look at some of the examples of experimental probability.

Example 1: Ben tried to toss a ping-pong ball in a cup using 10 trials, out of which he succeeded 4 times. 

P(win) $= \frac{Number of success}{Number of trials}$

             $= \frac{4}{10}$

             $= \frac{2}{5}$

Example 2: Two students are playing a game of die. They want to know how many times they land on 2 on the dice if the die is rolled 20 times in a row. 

The experimental probability of rolling a 2 

$= \frac{Number of times 2 appeared}{Number of trials}$

$= \frac{5}{20}$

$= \frac{1}{4}$

Fun Facts!

1. Probability of an event always lies between 0 and 1.

2. You can also express the probability as a decimal and a percentage.

Conclusion

Experimental probability is a probability that is determined by the results of a series of experiments. Learn more such interesting concepts at SplashLearn.

Solved Examples

1. Leo tosses a coin 25 times and observes that the “head” appears 10 times. What is the experimental probability of getting a head?

Solution:

 P(Head) $= \frac{Number of times heads appeared}{Total number of trials}$

               $= \frac{10}{25}$

               $= \frac{2}{5}$

               $= 0.4$

2. The number of cakes a baker makes per day in a week is given as 7, 8, 6, 10, 2, 8, 3. What is the probability that the baker makes less than 6 cakes the next day?

Solution: 

Number of cakes baked each day in a week $= 7, 8, 6, 10, 2, 8, 3$

Out of 7 days, there were 2 days (highlighted in bold) on which the baker made less than 6 cookies.

P$(< 6 $cookies$) = \frac{2}{7}$

3. The chart below shows the number of times a number was shown on the face of a tossed die. What was the probability of getting a 3 in this experiment?

Solution:

Number of times 3 showed $= 7$

Number of tosses $= 30$

P(3) $= \frac{7}{30}$

4. John kicked a ball 20 times. He kicked 16 field goals and missed 4 times. What is the experimental probability that John will kick a field goal during the game?

Solution: 

John succeeded in kicking 16 field goals. He attempted to kick a field goal 20 times. 

So, the number of trials $= 20$

John’s experimental probability of kicking a field goal $= \frac{Successful outcomes} {Trials attempted} = \frac{16}{20}$ 

$= \frac{4}{5}$

$= 0.8$ or $80%$

5. James recorded the color of bikes crossing his street. Of the 500 bikes, 10 were custom colors, 100 were white, 50 were red, 120 were black, 100 were silver, 60 were blue, and 60 were gray. What is the probability that the car crossing his street is white?

Solution: 

Number of white bikes $= 100$ 

Total number of bikes $= 500$

P(white bike) $=  \frac{100}{500} = \frac{1}{5}$

Practice Problems

Frequently Asked Questions