Centroid of a Triangle: Definition, Properties, Formula,  Examples

What Is the Centroid of a Triangle?

Centroid of a triangle is the point where the three medians of a triangle meet. It’s the point of intersection of three medians of a triangle. 

A median of a triangle joins a vertex to the midpoint of the opposite side. Thus, it bisects the opposite side. 

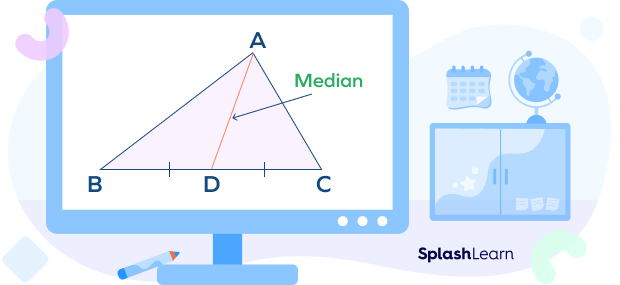
In the figure shown below, point G is called the centroid of the triangle ABC. It’s the point at which the medians of a triangle coincide.

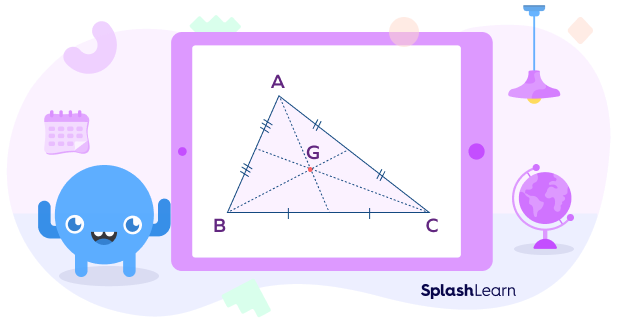
The Centroid of a Triangle: Definition

The point of concurrency of three medians of a triangle is known as the centroid of a triangle.

The centroid of a triangle intersects all three medians of a triangle in the ratio 2:1.

In the triangle ABC, the point G is the centroid. 

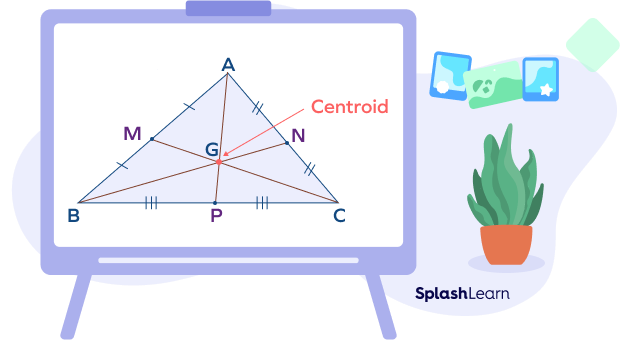
Centroid Theorem

According to the centroid theorem, the centroid of the triangle is at $\frac{2}{3}$ of the distance from the vertex to the midpoint of the opposite side.

In the triangle ABC,

$AG = \frac{2}{3} AD$

$BG = \frac{2}{3} BF$

$CG = \frac{2}{3} CE$

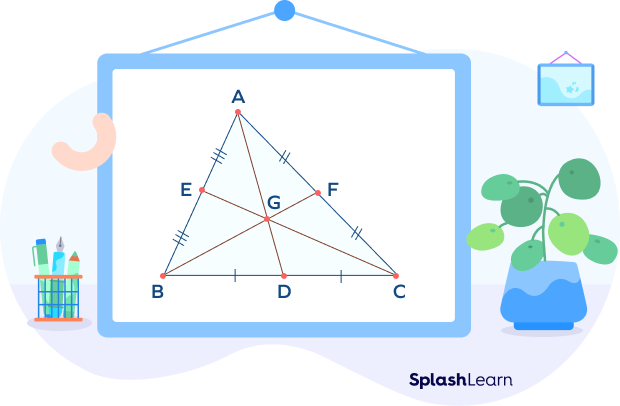
Properties of the Centroid of a Triangle

• The centroid is also known as the center of the object or the center of gravity.
• It is formed using the intersection of three medians of the triangle.
• The centroid of a triangle always lies inside the triangle.
• The centroid of a triangle divides all three medians into a 2:1 ratio.

How to Find the Centroid of a Triangle with Coordinates of Vertices

The centroid of a triangle can be found using the coordinates of the vertices of the given triangle. 

If the coordinates of the three vertices are known, then the coordinates of the centroid can be calculated by applying the centroid formula.

$G(x,y)= \bigg(\frac{x_1 + x_2+ x_3}{3},\; \frac{y_1 + y_2 + y_3}{3}\bigg)$

The Centroid of a Triangle Formula

Let us consider a triangle $\Delta ABC$ with vertices $A(x_1, y_1),\; B(x_2, y_2)$, and $C(x_3, y_3)$ as shown in the figure below.

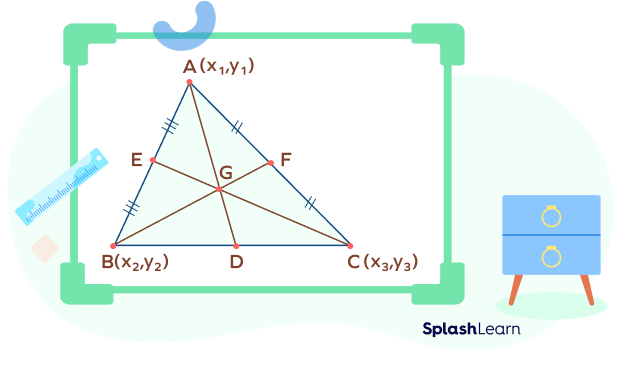
The formula for the centroid of a triangle is:

$G(x,y)= \bigg(\frac{x_1+ x_2+ x_3}{3},\; \frac{y_1+ y_2+ y_3}{3}\bigg)$

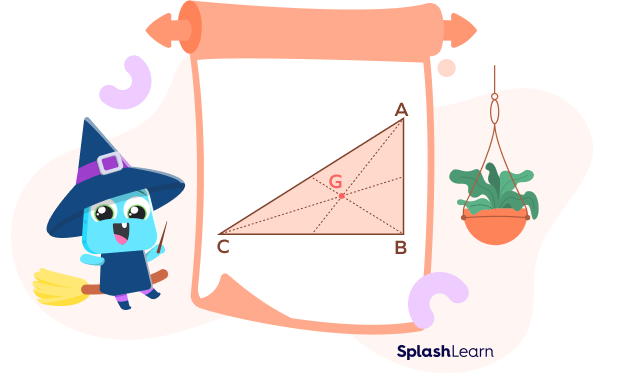
Centroid of a Right Triangle

The intersection of three medians, drawn from the vertices of the right-angled triangle to the midpoint of the opposite sides, is known as the centroid of a right-angle triangle. In the above figure, point G is called the centroid of the right angle triangle ABC.

Centroid and Orthocenter of a Triangle

The table below explains the four primary differences between a centroid and orthocenter of a triangle:

Centroid	Orthocenter
It always lies within the triangle.	It may lie outside of the triangle.
The point of intersection of the medians is known as the centroid.	The point of intersection of the altitudes is known as the orthocenter.
It is usually denoted by the letter “G.”	It is usually denoted by the letter “O.”
The centroid of a triangle intersects all three medians into a 2:1 ratio.	It does not divide the altitudes into any particular ratio.

Centroid and Incenter of a Triangle

Centroid	Incenter
It always lies within the triangle.	It lies inside the triangle.
It is the point of intersection of the medians.	It is the point of intersection of the angle bisectors of three interior angles.
It is usually denoted by the letter “G.”	It is usually denoted by the letter “I.”
The centroid of a triangle intersects all three medians into a 2:1 ratio.	It does not divide the angle bisectors into any particular ratio.

Derivation for the Formula of a Triangle’s Centroid (Proof)

Consider a triangle $\Delta ABC$ with vertices $A(x_1, y_1),\; B(x_2, y_2)$, and $C(x_3, y_3)$ as shown in the figure below.

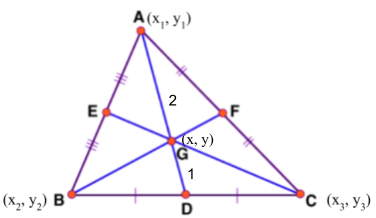
Let us derive the formula of a triangle’s centroid and prove that it is $(x,y) = \bigg(\frac{x_1+ x_2+ x_3}{3},\; \frac{y_1+ y_2+ y_3}{3}\bigg)$.

Since D is the midpoint of side BC of triangle ABC. 

So, by using the midpoint formula, we can find point D as $\bigg(\frac{x_2 + x_3}{2},\; \frac{y_2 + y_3}{ 2}\bigg)$.

As we know that the centroid G divides the median into 2:1 ratio. Thus, we can calculate the coordinates of point G using the section formula.

The x-coordinate of the centroid G is given by,

$x = \frac{\bigg[2\bigg(\frac{x_2 + x_3}{2}\bigg)+ 1\bigg(x_1\bigg)\bigg]}{2 + 1} = \frac{x_2+ x_3+ x_1}{3}$

$\Rightarrow x = \frac{x_1+ x_2+ x_3}{3}$

Similarly we can find the y-coordinate of the centroid G, which is given by, 

$y = \frac{\bigg[2\bigg(\frac{y_2 + y_3}{2}\bigg)+1\bigg(y1\bigg)\bigg]}{2 + 1} = \frac{y_2+ y_3+ y_1}{3}$

$\Rightarrow y = \frac{y_1 + y_2 + y_3}{3}$

Hence, the coordinates of the centroid G is $G(x,y) = \bigg(\frac{x_1 + x_2 + x_ 3}{3},\; \frac{y_1 + y_ 2 + y_3}{3}\bigg)$.

Facts about Centroid of a Triangle

• The centroid is also known as the center of the object or the center of gravity.
• Usually the centroid or center of gravity of a human is about an inch below the navel or the center of the body.
• The centroid of a triangle is at two-thirds length from the vertex of a triangle and at one-third from the midpoint of the opposite side.

Conclusion

In this article, we discussed the centroid of a triangle, its formula, derivations, the difference between orthocenter and centroid, and some facts and examples related to the centroid of a triangle.

Solved Examples on Centroid of a Triangle

1. In the following figure, check whether the point P represents the centroid of the triangle or not.

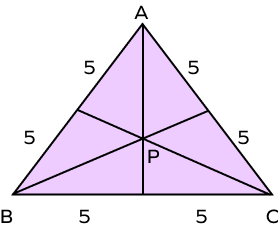
Solution:

In the given triangle ABC, all sides of the triangle are equal. Also, lines from the vertex to opposite sides divide the sides into equal parts. Hence, we can say that lines from the vertex meeting at point B are the medians. Thus, point P is the point of intersection of medians, that is, the centroid of triangle ABC.

2. Find the coordinates of the centroid of the triangle if the vertices of a triangle are given as $(2, 1), (3, 2)$, and $(–2, 4)$.

Solution:

Given, $(x_1, y_1) = (2, 1), (x_2, y_2) = (3, 2)$, and $(x_3, y_3) = (–2, 4)$.

The coordinates of the centroid are $G(x,y) = \bigg(\frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3}\bigg)$

$G(x,y) = \bigg(\frac{2+3\;-\;2}{3},\; \frac{1+2+4}{3}\bigg) = \bigg(1, \frac{7}{3}\bigg)$

3.  Find the coordinates of the centroid of the right angle triangle whose vertices are $(3,\; 2), (2, \;–\;3)$, and $(0,\; 0)$.

Solution:

Given, $(x_1, y_1) = (3, 2), (x_2, y_2) = (2, \;–\;3)$, and $(x_3, y_3) = (0, 0)$.

The coordinates of the centroid are $G(x,y) = \bigg(\frac{x_1 + x_2 + x_3}{3},\; \frac{y_1 + y_2 + y_3}{3}\bigg)$

$G(x,y) = \bigg(\frac{3+2+0}{3},\; \frac{2\;-\;3+0}{3}\bigg) = \bigg(\frac{5}{3},\; \frac{-1}{3}\bigg)$

4. In the triangle given below if G is the centroid and AG = 12 inches. Find the length of the line segment GD and the length of the median.

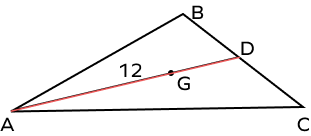
Solution:

Given, G is the centroid and $AG = 12$ inches.

As we know, the distance from the vertex to the centroid $= \frac{2}{3} \times$ the length of the median.

$\Rightarrow AG = \frac{2}{3} \times AD$

$\Rightarrow 12 = \frac{2}{3} \times AD$

$\Rightarrow AD = \frac{36}{2} = 18$

Hence, the length of the median $= 18$ inches.

Also as we know, the centroid divides the median in the ratio 2:1.

$\Rightarrow GD = \frac{1}{2} \times AG$

$\Rightarrow GD = \frac{1}{2} \times 12 = 6$ inches.

Practice Problems on Centroid of a Triangle

Frequently Asked Questions on Centroid of a Triangle