What Is a Constant? Definition, Solved Examples, Facts

What Is a Constant in Math?

A “constant” simply means a fixed value or a value that does not change. A constant has a known value. 

If you measure the height of a wall or bookshelf at home, it will be a constant number. It won’t change. However, if you measure the height of a plant in a pot, it will keep changing as it grows. It’s not constant.

Take a look at the following sentences to understand this.

• There are 7 days in a week. Here,$\Rightarrow 7$ is a constant.
• July 4 is celebrated as Independence Day in the USA$\Rightarrow $. Here, 4 is a constant.

Constant: Definition

What Is a Constant Term in Algebraic Expression?

Constant term plays an important role In algebraic expressions or equations. 

Consider an algebraic equation: $5x + 4y = 12$ 

Here,

• x, y are variables. Variable is a quantity that can be changed.
• 5 is the coefficient of x. 4 is the coefficient of y.
• 12 and 1 are constants.

5 and 4 are also numbers. Are they constants in this equation? — The answer is no. They are not constants. They are coefficients of the variables. We multiply the coefficient with whatever value gets assigned to the variable.

How to Recognize a Constant in Algebraic Expression

• It is a known value.
• It’s a stand-alone number.
• Even if the value is unknown, it is a set number.
• It involves fractions, decimals, whole numbers, all real numbers.
• An exponent is not a constant. For example, in the term $2^5$, 5 is not a constant. 

Constant Numbers

All numbers are constant numbers. In math, real numbers, natural numbers, whole numbers, and integers are all constant numbers. They cannot take a different value.

Example: Ron read 5 pages of a book on Monday and 8 pages on Tuesday. How many pages did he read in two days?

Here, to find the total number of pages read by Ron, we have to add 5 and 8, which are constant numbers. They cannot take any other value.

Total number of pages read in the two days $= 5 + 8 = 13$ pages

Again, 13 is also a constant!

Arbitrary Constants

They are symbols that can have different values assigned to it, but are unaffected by changes in the values of a variable in the equation. Sometimes, English alphabets are used to represent fixed values, which are unknown. 

Example: $y = mx + c$ is the general equation of a straight line, where m and c are arbitrary constants. 

m: the slope of the line

c: the y intercept.

If $m = 2$ and $c = 1$, we get the equation of a line as $y = 2x + 1$.

Constant v. Variable

Constant	Variable
It has a known value.	It does not have a fixed value.
The value is fixed and does not change over time.	It can take any value.
The symbols are usually numbers. Some famous constants such as pi are often identified using a standard symbol.	Different English alphabets are used to represent a variable.
Examples: $90,\; 6\;, \;-45\;$, etc	Examples: x, 5y, 9z

Constant Function

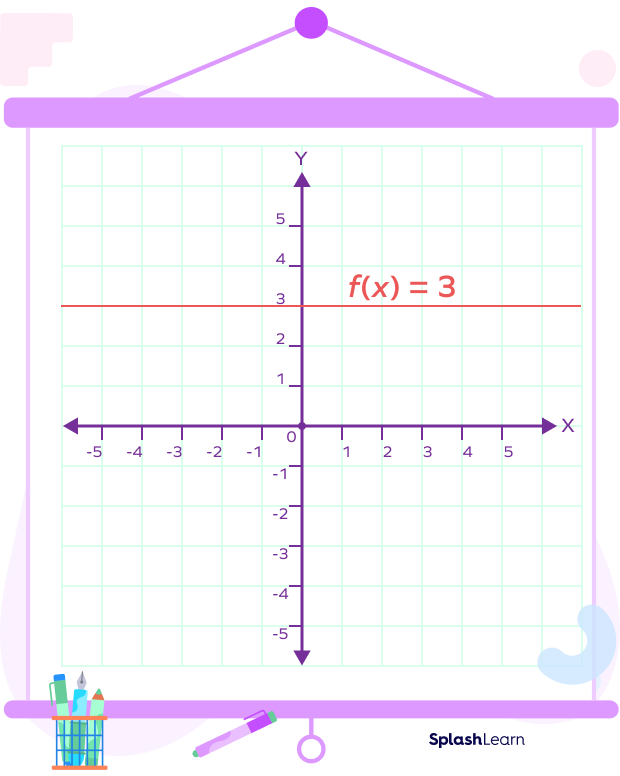
A constant function is a function that maps every number to a constant. Thus, the output is the constant number or the same for any input value.

We denote the constant function as: $f(x) = c$.

Suppose $c=3$

$f(x) = 3$

This is a constant function because the variable is x, and the constant 10 is not dependent on x. No matter what value of x we put in the equation, the output of the function will always be 10, since x does not appear in the function.

Mathematical Constants

We use the term mathematical constant to describe fixed, well-defined numbers. Some of mathematical constants include:

• $\pi = 3.1415926536$…
• $i^2 = \;-1$
• e = 2.7182818284…
• Pythagoras’ constant: $\sqrt{2} = 1.4142135623$…
• Theodorus’ constant: $\sqrt{3} = 1.7320508075$…
• Golden ratio: $\theta = 1.618033$…

Constants Written as Variables

A constant is commonly denoted a “c” to represent a fixed value when the exact value is not known in an expression or a word problem. 

Here, “c” is the variable, but its value will always be a “fixed number” when actually writing a polynomial or expression. 

Consider the quadratic equation of the form: $ax^2 + bx + c = 0$.

Here, a and b are coefficients of the variable x.

Here, c is a constant (the constant term of the polynomial). 

Note: a, b, and c are also called parameters since they are used to represent a model or a family of quadratic equations. Parameters may take multiple values, but they do not change once assigned forming a particular function. When parameters are changed, we get a different function or equation. 

Solved Examples on Constants

1. Find the constant in the algebraic expression $3x^2y\;-\;4xy + 5y +10$.

Solution:

Given expression: $3x^2y\;-\;4xy + 5y + 10$

The only term that is fixed is 10.

So, the constant is 10.

2. Why is 15 a constant?

Solution: 

15 is a constant because 15 is an integer, it is a fixed value and it will not change.

3. In the equation $3x\;-\;5 = y$, which is the constant?

Solution: 

There are three terms: $3x,\;-\;5$, and y.

x and y are variables.

$– 5$ is a fixed value or does not change. 

So, $– 5$ is a constant. 

5. James took 4 hours to travel from Place A to Place B, whereas Jack took 3 hours to cover the same distance. Which are the constants and variables in this statistical scenario?

Solution: 

The distance between Place A and Place B is constant. 

The time taken is a variable. 

Practice Problems on Constants

Frequently Asked Questions on Constants