What Is a Convex Polygon?
A convex polygon is a polygon with all interior angles less than $180^\circ$ and vertices are pointed outwards.
In convex polygons, all diagonals are in the interior of the polygon. All the vertices of a complex polygon point outwards. A regular polygon in geometry is always convex. Any closed shape that has a curved surface is convex. Take a look at the image given below to understand it better.
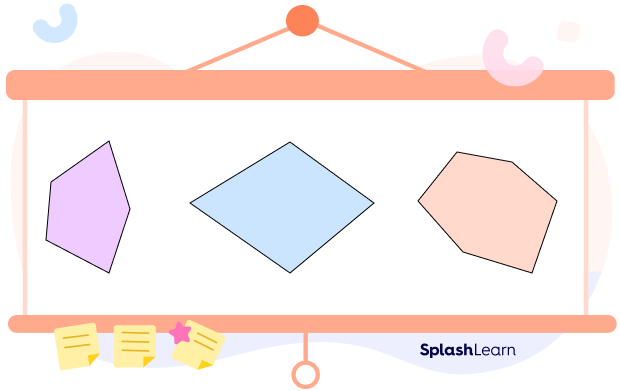
In geometry, a polygon is a flat or plane, two-dimensional, closed shape bounded with straight sides, with at least three sides and angles. All polygons can be broadly divided into two groups based on the measure of their internal angles: convex and concave. Just like a convex mirror, a convex polygon curves outward. Let us learn more about the convex polygon, its formula, properties, types, and examples.
Definition of a Convex Polygon
Convex polygon is defined as a closed figure having all the interior angles less than $180^\circ$
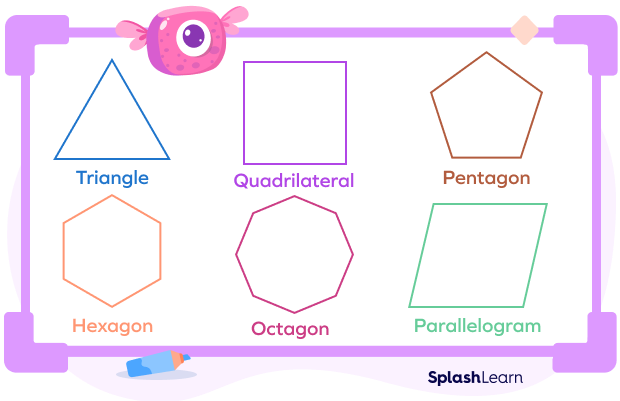
This means that all the vertices of the polygon will point outwards, away from the interior of the shape. No sides are pointing inward. A triangle is considered an important convex polygon. Other convex polygon shapes are quadrilateral, pentagon, hexagon, parallelogram, etc.
Recommended Games
Properties of a Convex Polygon
- The diagonals of a convex polygon lie inside the polygon.
- The internal angles of a convex polygon are always less than $180^\circ$.
- A polygon is considered convex if the line connecting every pair of its points lies entirely within it.
- The sum of the interior angles of a convex polygon of sides “n” is given as $180(n\;-\;2)^\circ$.
- To calculate the area of the convex polygon, the polygon is divided into triangles and then the area of each triangle is summed up.
Types of Convex Polygons
Convex polygons can be divided into two types. They are as follows:
1. Regular convex polygon
2. Irregular convex polygon
Regular Convex Polygon
A regular convex polygon (or a convex regular polygon) is one with equal sides and congruent interior angles that are less than 180 degrees. In a regular polygon, the vertices are equidistant from the center.

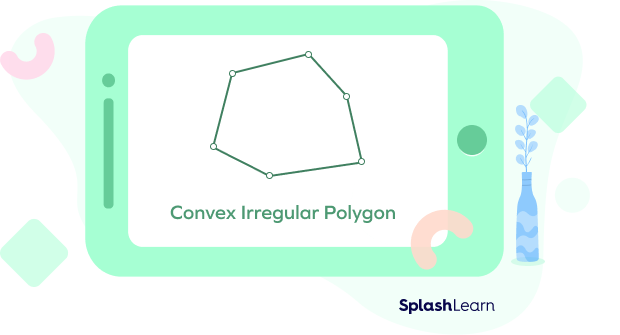
Irregular Convex Polygon
Each side of an irregular convex polygon has a different length, and all of the internal angles have different measurements.
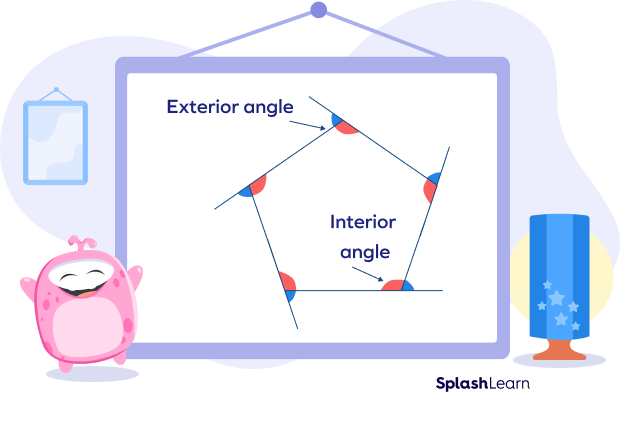
Interior Angles of a Convex Polygon
The interior angles of a polygon are the angles inside the polygon. A polygon has the same number of interior angles as its sides.
Exterior Angles of a Convex Polygon
The exterior angles of a polygon are the angles formed by extending the sides of a polygon. The sum of the exterior angles of a polygon is $360^\circ$.
Convex Polygon Formulas
Let’s see some formulas related to convex polygons.
Perimeter of Regular Convex Polygon
The total distance of the outer sides of a closed figure is known as the perimeter. It is the total length of all sides of a polygon. A regular polygon has all sides equal. Therefore, we can find the perimeter of a regular polygon by repeated addition.
The formula to calculate the perimeter of regular convex polygon is as follows:
Perimeter $= n \times s$
Where, $n =$ Number of sides
$s =$ Length of sides
Perimeter of Irregular Convex Polygon
It is the total distance around a polygon. It can be found by adding together all the sides of the polygon.
The formula to calculate the perimeter of irregular convex polygon is as follows:
Perimeter $=$ Sum of all sides
Sum of Interior Angles of a Convex Polygon
The sum of interior angles of a convex polygon with “n” sides is given by the formula, 180(n-2).
For example, a square has 4 sides. Thus, $n = 4$
So, the sum of its interior angles $= 180^\circ (4\;-\;2) = 360^\circ$.
Sum of Exterior Angles of a Convex Polygon
Sum of exterior angles of a polygon is $360^\circ$.
Each exterior angle of a convex polygon is equal to $\frac{360^\circ}{n}$.
Here “n” is the number of sides of the polygon.
For example, a square has 4 sides. So each exterior angle is $\frac{360^\circ}{4}$, which is equal to $90^\circ$.
Difference between Concave Polygon and Convex Polygon
Take a look at the image given below to see the real life examples of convex and concave polygons.
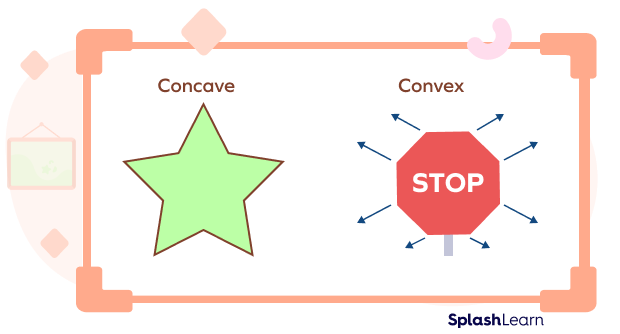
The difference between a concave and convex polygon are as follows:
| Convex Polygon | Concave Polygon |
|---|---|
| A convex polygon has all its interior angles less than 180 degrees. | A concave polygon has at least one interior angle more than 180 degrees. |
A convex polygon has no diagonal in the exterior.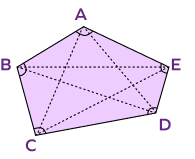 | Concave polygons have portions of diagonals in the exterior.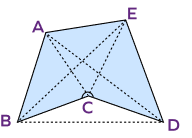 |
| All sides point outwards. There are no dents. | Some sides point inward. There are dents. |
| The line joining any two vertices of the convex polygon lies completely within it. | A line joining two vertices of a concave polygon may or may not lie within the polygon. |
| Convex polygons can be regular or irregular. | Concave polygons are never regular. |
Facts about Convex Polygon
- Convex polygon is defined as a polygon with all its interior angles less than or equal to 180 degree.
- Based on the shape of the polygon, the types of a polygon are convex and concave, regular and irregular, simple and complex.
- A regular polygon in geometry is always a convex polygon.
- Convex polygons are easier to draw in comparison to concave polygons.
- The sum of the interior angles of a convex polygon is by the formula $180(n\;-\;2)^\circ$.
- The sum of the exterior angles of a convex polygon is given as $\frac{360^\circ}{n}$.
Solved Examples on Convex Polygon
1. Find the perimeter of the regular decagon if the length of the side is 10 in.
Solution:
Decagon is a regular polygon with 10 sides.
$s = 10$
$n = 10$
We know that,
Perimeter of convex polygon$ = n \times s$
Thus, Perimeter $= 10 \times 10$
$= 100$ in.
2. What is the measure of an interior angle of a regular convex polygon like a hexagon?
Solution:
The number of sides of a hexagon is $n = 6$
We know that the formula for the sum of all interior angles of a polygon of n sides is
$180 (n\;-\;2)^\circ$.
Thus, the sum of the interior angles of the hexagon is:
$180 \times (6\;-\;2)^\circ = 180 × (4)^\circ$
$= 720^\circ$
Since the given hexagon is regular, all 6 interior angles measure the same. Therefore, the measure of each interior angle is $\frac{720}{6} = 120^\circ$
Thus, the required angle $= 120^\circ$.
3. The interior angles of a pentagon are $x^\circ,\; x^\circ,\; 2x^\circ,\; 2x^\circ$ and $3x^\circ$. What is x ?
Solution:
We know that, a pentagon has 5 sides and has interior angles that sum to $(5 \;-\; 2) \times 180^\circ = 540^\circ$
Writing the equation for the above example,
$x^\circ + x^\circ + 2x^\circ + 2x^\circ + 3x^\circ = 540^\circ$
$9x^\circ = 540^\circ$
$x = \frac{540}{9}$
$x = 60^\circ$.
4. Find the value of x in the given figure:
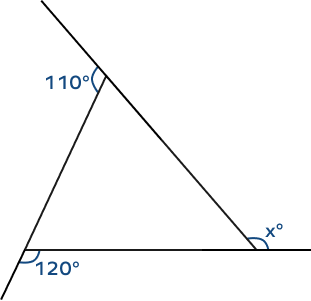
Solution:
We know that, sum of exterior angles of a polygon is $360^\circ$.
Thus, $110^\circ + 120^\circ + x = 360^\circ$
$230^\circ + x^\circ = 360^\circ$
$x^\circ = 360^\circ \;-\; 230^\circ$
$x^\circ = 130^\circ$
Practice Problems on Convex Polygon
Convex Polygon - Definition, Formula, Properties, Types, Examples
The name of the four sided regular convex polygon is ________________.
A regular convex polygon is a polygon where each side is of equal length, and all the interior angles are equivalent and less than $180^\circ$. Thus, square is a regular convex polygon
What is the type of a polygon represented by the three polygons in the following image?
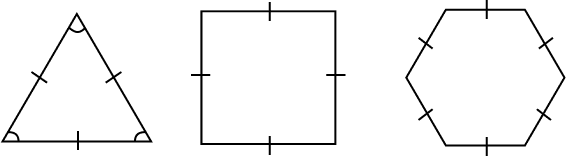
The image shows a triangle with three equal interior angles, a square and a regular hexagon.
A regular convex polygon is a polygon where each side is of equal length, and all the interior angles are equal and less than $180^\circ$.
Each interior angle of a convex polygon is
A convex polygon is a polygon with all interior angles less than $180^\circ$
Each exterior angle of the square is _________.
Each exterior angle of a convex polygon is equal to $\frac{360^\circ}{n}$. Here, “n” is the number of sides of the polygon. A square has 4 sides. So, each exterior angle is $\frac{360^\circ}{4}$, which is equal to $90^\circ$.
Three geometric shapes are given below. Which figure is convex?
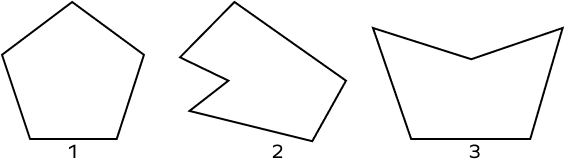
Convex polygon is defined as a closed figure having all the interior angles less than 180. This means that all the vertices of the polygon will point outwards, away from the interior of the shape. Thus, only figure 1 is a convex polygon.
Frequently Asked Questions on Convex Polygons
What are some real-life examples of convex polygons?
Convex polygons can be seen in everyday life in our surroundings. Some real-life examples include stop signs on the roads, hexagons and pentagons on a football, a coin, etc.

How do you tell whether the polygon is concave or convex?
If a line drawn that passes through the polygon passes through only two sides, then the shape of the polygon is convex. On the other hand, if you can draw a line that can pass through more than two sides, it is a concave polygon. In 3-dimensional shapes, the same test can be performed to differentiate between the two.
What are simple and complex polygons?
A simple polygon has only one boundary, and it doesn’t cross over itself. The sides of a simple polygon do not intersect. A complex polygon is a polygon whose sides cross over each other one or more times.

Is a triangle a convex or concave polygon?
A polygon is convex if all the interior angles are less than 180 degrees. If one or more of the interior angles is more than 180 degrees, the polygon is concave. A triangle is a geometric shape with three sides. In a triangle, the sum of all interior angles is itself 180°. Thus, a triangle is a convex polygon.
Can a concave polygon be a regular polygon?
No. In concave polygon, interior angle measures greater than $180^\circ$ and one diagonal lies outside the polygon. In regular polygons, all sides are equal in length and all the interior angles are of equal measure. So, a concave polygon will not be a regular polygon.
Is a triangle convex or concave?
A triangle is always convex. A triangle can never be a concave polygon.


















