Diagonals of Parallelogram: Formula, Examples

What Are Diagonals of a Parallelogram?

Line segments connecting two non-adjacent vertices of a parallelogram are called “diagonals of a parallelogram.” 

A quadrilateral with opposite sides that are parallel and equal is known as a parallelogram. Its opposite angles are also equal. 

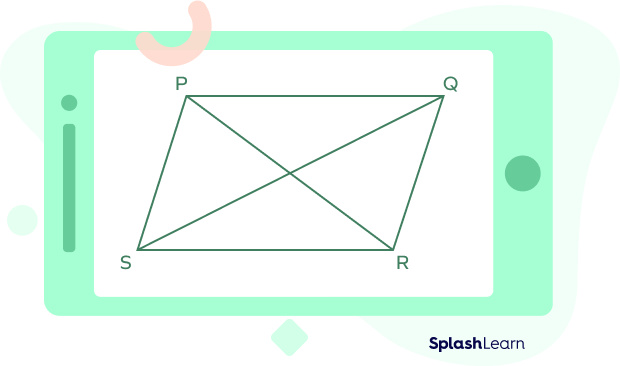
A parallelogram has two diagonals. The diagonals of a parallelogram connect the opposite vertices. 

Square, rectangle, rhombus are examples of a parallelogram.

Properties of Diagonals of a Parallelogram

• Diagonals of a parallelogram bisect each other.
• The diagonals of a square bisect each other at right angles.
• The diagonals of a rectangle bisect each other, but not at right angles. 
• The diagonals of a rhombus are perpendicular to each other.
• Each diagonal divides the parallelogram in two congruent triangles.

Diagonals of Parallelogram Formula  

Let’s discuss two important formulas.

Finding Lengths of Diagonals of a Parallelogram

The above figure shows a parallelogram and its two diagonals. 

p & q are diagonals.

x & y are two adjacent sides of a parallelogram. 

$\angle \text{A}$ & $\angle\text{B}$ are the interior angles of a given parallelogram. 

How can we calculate the length of diagonals of a parallelogram?

The length of the diagonal of the parallelogram can be calculated by using the following formulas:

$p = \sqrt{x^{2} + y^{2}\;-\;2xy\; cos\;(A)} = \sqrt{x^{2} + y^{2} + 2xy\; cos\;(B)}$

$q = \sqrt{x^{2} + y^{2} + 2xy\; cos\;(A)} = \sqrt{x^{2} + y^{2} \;-\; 2xy\; cos\;(B)}$

If the measurement of two sides and one interior angle is given the above formula can be used for finding the length of diagonal of the parallelogram.

Relationship Between Sides and Diagonals of a Parallelogram

$p^{2} + q^{2} = 2 (x^{2} + y^{2})$

Here, Here, p & q are the diagonals of parallelogram

x & y are the adjacent sides of a parallelogram

If the measurement of two adjacent sides & one diagonal is given then the above formula can be used for finding the length of another diagonal of the parallelogram.

Fun Facts!

• The diagonals of a parallelogram bisect each other at the point of intersection.
• The length of the diagonals of a parallelogram is not equal.

Conclusion

This article gives a brief description of the diagonals of parallelograms, and how to calculate the length of diagonals of parallelograms. Let’s solve a few examples and practice problems.

Solved Examples on Diagonals of Parallelogram

1. Determine the length of diagonals of a parallelogram with side lengths 4 ft, 8 ft,  and angle $60^{\circ}$.

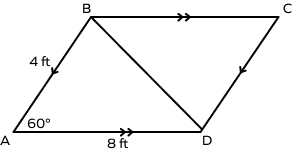
Solution: 

Here x $= 4$  ft & y $= 8$  ft

                      $\text{m} \angle \text{A} = 60^{\circ}$ 

Formula for calculating the length of diagonals is given as,

$p = \sqrt{x^{2} + y^{2}\;-\;2xy\; cosA}$

$= \sqrt{4^{2} + 8^{2} \;-\; 2(4)(8)\; cos(60^{\circ})}$

$= 6.92$ ft

$q = \sqrt{x^{2} + y^{2} + 2xy\; cosA}$

$ = \sqrt{4^{2} + 8^{2} + 2(4)(8)\; cos(60^{\circ})}$

$= 10.58$ ft

2. Determine the length of diagonals of a parallelogram with sides 3 inches and 6 inches, and the interior angle is 300.

Solution: 

Here,  x $= 3$ inches & y $= 6$ inches

              Also,   $\text{m}\;\angle\text{A} =30^{\circ}$

Formula for calculating the length of diagonals of the parallelogram is given as, 

$p = \sqrt{x^{2} + y^{2}\;-\;2xy\; cosA}$

$= \sqrt{3^{2} + 6^{2}\;-\;2(3)(6)\; cos\;30^{\circ}}$

$= 3.71$ inches

$q = \sqrt{x^{2} + y^{2} + 2xy\; cosA}$

$= \sqrt{3^{2} + 6^{2} + 2(3)(6)\; cos\;(30^{\circ})}$

$= 8.72$ inches

3. Determine the length of any one diagonal of a parallelogram if the length of the sides of a parallelogram and interior angle are 4 ft, 7 ft and 50o.

Solution: 

Given: Here,  x $= 4$ ft and y $= 7$  ft

              Also,    $\angle\text{A} = 50^{\circ}$

Formula for calculating the length of diagonals of the parallelogram is given as, 

$p = \sqrt{x^{2} + y^{2}\;-\;2xy\; cosA}$

$= \sqrt{4^{2} + 7^{2}\;-\;2(4)(7)\; cos(50^{\circ})}$

 $=  5.38$ ft

4. Determine the length of any one of the diagonals of a parallelogram having a length of sides 5ft, 7 ft, and one of the interior angles 450.

Solution: 

Here,  x $= 5$ ft & y $= 7$  ft

              Also,  $\angle\text{A} = 45^{\circ}$

Formula for calculating the length of diagonals of the parallelogram is given as, 

$p = \sqrt{x^{2} + y^{2}\;-\;2xy\; cos(A)}$

$= \sqrt{5^{2} + 7^{2}\;-\;2(5)(7)\; cos(45^{\circ})}$

$=  4.95$ ft

5. Determine the length of a diagonal of  a parallelogram with a side length of 5 ft and 8 ft if the length of another diagonal is 10 ft.

Solution:

Given: x $= 5$  ft,  y $= 8$  ft & p $= 10$  ft

As we know, the length of two sides and one diagonal is given for finding the length of another diagonal. We will use the formula of the relationship between the sides and diagonals of a parallelogram.

By using the formula,

$p^{2} + q^{2} = 2(x^{2} + y^{2})$

$\Rightarrow 10^{2} + q^{2} = 2(5^{2} + 8^{2})$

$\Rightarrow 100 + q^{2} = 2(25 + 64)$

$\Rightarrow 100 + q^{2} = 178$

$\Rightarrow q^{2} = 178\;-\;100$

$\Rightarrow q^{2} = 78$ 

By taking a square root,

$\Rightarrow q = 8.83$ ft

Practice Problems on Diagonals of Parallelogram

Frequently Asked Questions on Diagonals of Parallelogram