What Are Diagonals of a Rectangle?
Diagonals of a rectangle are line segments connecting opposite vertices of a rectangle. A rectangle is a quadrilateral in which opposite sides are equal and all angles measure $90^\circ$.
A diagonal is a line segment connecting two non-adjacent vertices of a polygon. The word diagonal comes from the ancient Greek word “diagonios,” (Latin diagonalis) which means “from angle to angle.”
Both Euclid and Strabo used it to describe a line that connects two vertices of a cuboid or a rhombus; later, it became known in Latin as diagonus (slanting line).

Diagonals of a Rectangle Definition
A line segment that connects any two opposite vertices of a rectangle is called diagonal of a rectangle.
Consider ▭ABCD. A rectangle with diagonals AC and BD as shown below.
Here, $AC = BD$.

Recommended Games
Properties of Diagonals of a Rectangle
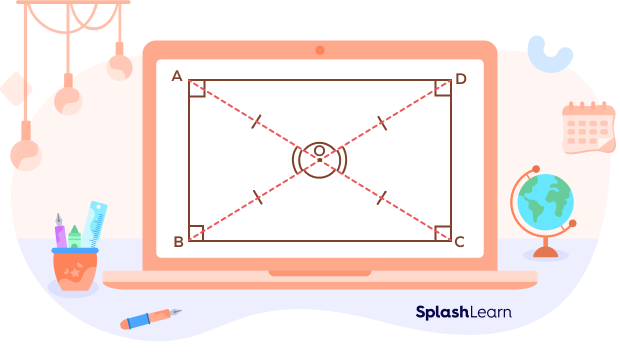
- The diagonals of a rectangle are congruent.
$\left[AC = BD\right]$
- Each diagonal divides a rectangle into two congruent right-angled triangles.
- The diagonals of a rectangle are not perpendicular to each other.
- If two diagonals of a rectangle bisect each other at $90^\circ$, it is called a square.
- When two diagonals intersect, they form one obtuse angle and one acute angle. The opposite central angles are equal.
- Adjacent angles formed by the diagonals are supplementary.
- Diagonals of a rectangle form the hypotenuse of the right triangle.
Recommended Worksheets
Diagonal of a Rectangle Formula
The diagonal of a rectangle formula helps in finding the length of the diagonal when the length and width of the rectangle are known.
A diagonal divides a rectangle into two right triangles, each of which has a hypotenuse and sides that are equal to the sides of the rectangle. The diagonal is that hypotenuse.
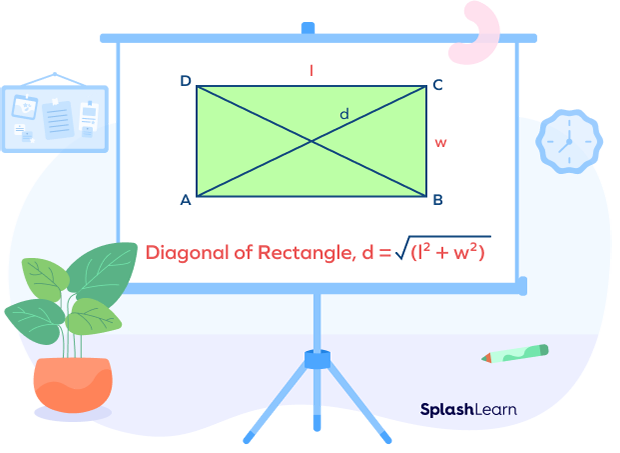
So, how to find the diagonal of a rectangle? What is the diagonal measurement of a rectangle?
The diagonal length of a rectangle is calculated using the formula, $d = \sqrt{(w^2 + l^2)}$
where, $d = diagonal$
$l = length$
$w = width$
This formula can be used to find the measurement of the length of a diagonal of a rectangle.
Diagonal of a Rectangle Formula Derivation
The diagonal of a rectangle formula is derived using the Pythagoras’ Theorem. Split the rectangle into two right triangles formed by a diagonal.
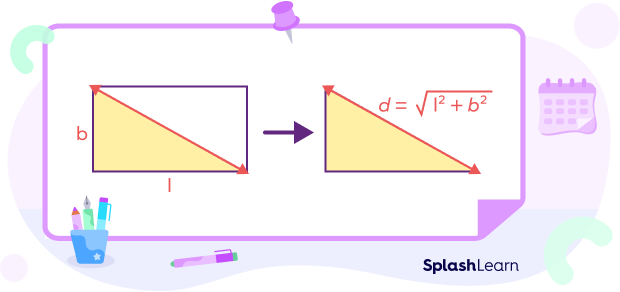
Applying Pythagoras’ Theorem in the right triangle PSR, we have
$d^2 = b^2 + l^2$
Here, $d =$ diagonal, $l =$ length, $b =$ breadth
Taking square root on both sides,
$d = \sqrt{(b^2 + l^2)}$
- $l =$ length of the rectangle
- $b =$ breadth of the rectangle
Simply substitute the values of the length and breadth in the formula to get the answer.
Example:
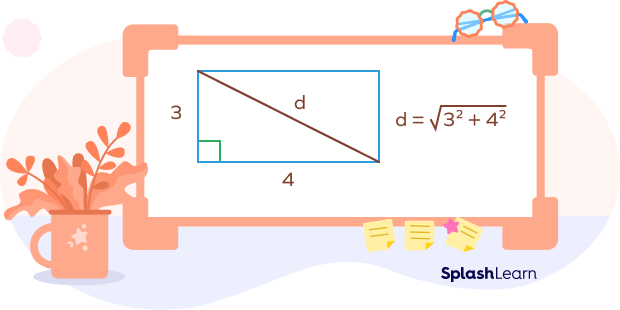
In the above rectangle,
Length of diagonal $= d = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5$ units
Angles Made by Diagonals of a Rectangle
As discussed above, if the diagonals of the polygon bisect each other, it is called a square.
Diagonals of a rectangle are equal in length, bisect each other. They do not meet at a right angle in the center. The diagonals of a rectangle do not bisect the interior angles of the rectangle.
Example: Take a look at the image given below.
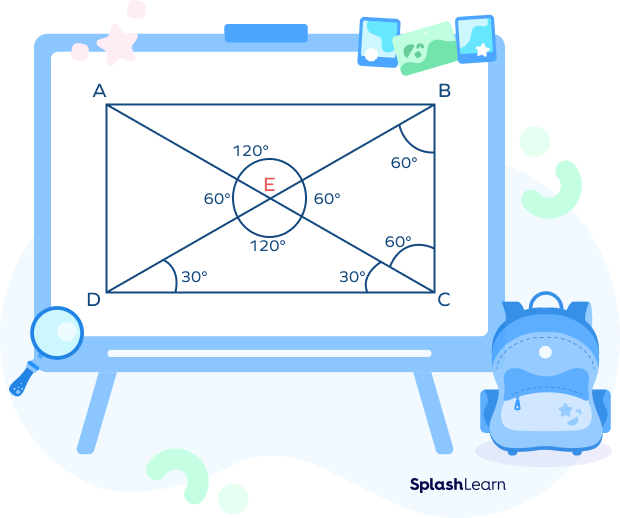
In the image given above, AC and BD are the diagonals.
Angles formed by diagonal AC and BD are $\angle AED,\; \angle AEB,\; \angle BEC$, and $\angle DEC$.
These angles do not meet at right angles, but the adjacent angles are supplementary, which means the adjacent angle-pairs add up to $180^\circ$.
- $\angle AED + \angle AEB = 180^\circ$
- $\angle AEB + \angle BEC = 180^\circ$
- $\angle BEC + \angle DEC = 180^\circ$
- $\angle AED + \angle DEC = 180^\circ$
Facts about Diagonals of a Rectangle
- The two diagonals of a rectangle divide the rectangle into four triangles.
- Each diagonal of a rectangle divides it into two congruent right triangles.
- The intersection of the diagonals is the circumcenter. That is, you can draw a circle with that at the center to pass through the four corners.
Thus, diagonal $= 2r$ …where r is the radius of the circumcircle
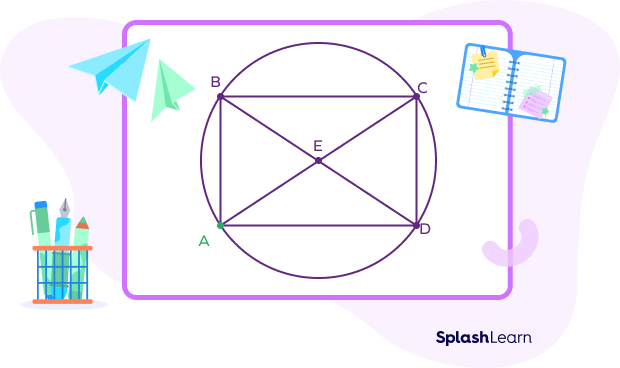
- We can calculate the length of the diagonal of the rectangle using the formula:
$d = \sqrt{(b^2 + l^2)}$
- The rectangle is called a square if its diagonals bisect each other at right angles.
- As the diagonals are generally slanted, a slanted symbol “ / ” is used to denote diagonals.
Conclusion
In this article, we have learned about diagonals of the rectangle, its properties, formulas, and facts. Now let’s solve some examples based on the formulas learned above.
Solved Examples for Diagonals of a Rectangle
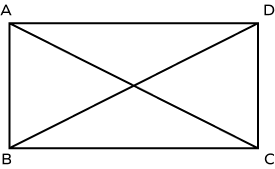
1. Identify the length, width and diagonal in the given rectangle.
Solution:
Length $\rightarrow$ AD and BC
Width $\rightarrow$ AB and CD
Diagonals $\rightarrow$ AC and BD
2. Find the length of each diagonal of a rectangle of length 15 units and width 8 units.
Solution:
Length of the rectangle, $l = 15$ units.
Breadth of the rectangle, $b = 8$ units.
Length of the diagonal $= d = \sqrt{(b^2 + l^2)}$
$d = \sqrt{(8^2 + 15^2)}$
$d = \sqrt{(64 + 225)}$
$d = \sqrt{289}$
$d = 17$ units.
The length of the diagonal is 17 units.
3. A rectangular park is 30 ft long and 16 ft wide. Determine the diagonal of the rectangular park.
Solution:
Length of the rectangular park $= 30$ ft
Breadth of the rectangular park $= 15$ ft
Length of the diagonal $d = \sqrt{(b^2 + l^2)}$
$= sqrt{(16^2 + 30^2)}$
$= \sqrt{(256+ 900)}$
$= \sqrt{1156}$
$= 34$ ft
The diagonal of the rectangular park is 34 ft.
4. Find the length of the diagonal of the given rectangle.
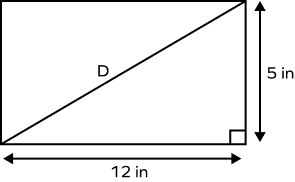
Solution:
Length $= 12$ in
Breadth $= 5$ in
Diagonal $= ?$
Using the Pythagorean theorem, we get:
$l^2 + b^2 = d^2$
$12^2 + 5^2 = d^2$
$d^2 = 144 + 25$
$d^2 = 169$
Taking the square root
$d = 13$ in
5. Find the length of the rectangle if the breadth of the rectangle is 3 inches, and the diagonal of the rectangle is 5 inches.
Solution:
Breadth of the rectangle $= 3$ in
Diagonal of the rectangle (hypotenuse) $= 5$ in
Here we will apply Pythagoras’ Theorem.
$(Hypotenuse)^2 = (Length)^2 + (Breadth)^2$
$5^2 = l^2 + 3^2$
$l^2 = 5^2 \;-\; 3^2$
$l^2 = 25 \;-\; 9$
$l = \sqrt{16}$
$l = 4$ in
Length of the rectangle is 4 inches.
Practice Problems on Diagonals of a Rectangle
Diagonal of a Rectangle - Properties, Formula, Examples, FAQs
A line segment that connects any two opposite vertices of a rectangle is said to be its _________.
A line segment that connects any two opposite vertices of a rectangle is said to be its diagonal.
The diagonals of a rectangle are ______.
The diagonals of a rectangle are equal in length.
Which of the following is NOT TRUE ?
The diagonals of a rectangle are not perpendicular to each other. When two diagonals bisect each other at $90^\circ$, it is called a square.
The length of diagonals of the rectangle is calculated using formula _________.
The length of diagonals of the rectangle is calculated using formula: $d = \sqrt{(b^2 + l^2)}$
where, $d =$ diagonal of rectangle
$l =$ length of the rectangle
$b =$ breadth of the rectangle
Adjacent angles formed by the diagonals of a rectangle are ________.
Adjacent angles formed by the diagonals are supplementary.
Frequently Asked Questions about Diagonals of a Rectangle
Why are the diagonals of a rectangle equal in length?
A rectangle is a quadrilateral where all the angles are right angles. A rectangle is also a parallelogram where the opposite sides are equal.
Consider this rectangle ABCD.
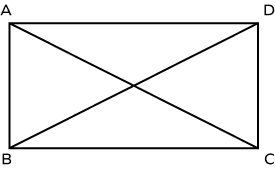
In the above rectangle, consider triangles ABC and DCB.
$\angle ABC = \angle DCB = 90$ [Angles of rectangle]
$BC = BC$ (common side)
$AB = DC$ (Opposite sides of a parallelogram are equal)
Hence, $ABC\congDCB$
$AC = DB$ [CPCTC]
Hence, the diagonals of a rectangle are equal.
Do diagonals of a rectangle always bisect each other?
The diagonals of a rectangle always bisect each other. However, they do not meet at 90 degrees except if the rectangle is a square.
What is the formula for the area of a rectangle?
Area of a rectangle is given by the product of length and breadth.Area of rectangle $= l\timesb$
Why is the area of the rectangle the product of length and breadth?
Let us understand why the area of the rectangle is $length \times breadth$.
Consider ▭ ABCD. We can see that the diagonal AC divides the rectangle into two congruent triangles, $\Delta ABC$ and $\Delta ADC$.
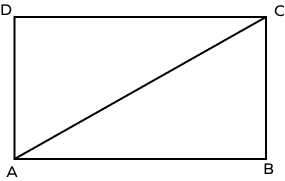
Area of Rectangle $ABCD =$ Area of Triangle $ABC +$ Area of Triangle ADC
$= 2\times$ Area of Triangle ABC
$= 2 \times (\frac{1}{2} \times Base \times Height)$
$= AB \times BC$
$= Length \times Breadth$
The area of the rectangle is the product of length and breadth.
How many diagonals are there in a rectangle? Are the diagonals of a rectangle always congruent?
A rectangle has two diagonals. Each diagonal divides a rectangle into two right triangles. The two diagonals of a rectangle are always congruent.
Are diagonals perpendicular in a rectangle?
No! The two diagonals of a rectangle do not intersect at right angles.
























