- What Is a Rectangle and a Parallelogram?
- Properties of a Rectangle and a Parallelogram
- Difference between a Parallelogram and a Rectangle Chart
- Solved Examples on Difference between Rectangle and Parallelogram
- Practice Problems on Difference between Rectangle and Parallelogram
- Frequently Asked Questions on the Difference between Rectangle and Parallelogram
What Is the Difference between Rectangle and Parallelogram?
A quadrilateral is a polygon having four sides, four angles, and four vertices. There are various types of quadrilaterals. Parallelograms and rectangles are both quadrilaterals.
To understand the difference between rectangle and parallelogram, take a look at the following image. Here, PQRS is the rectangle, and ABCD is the parallelogram.
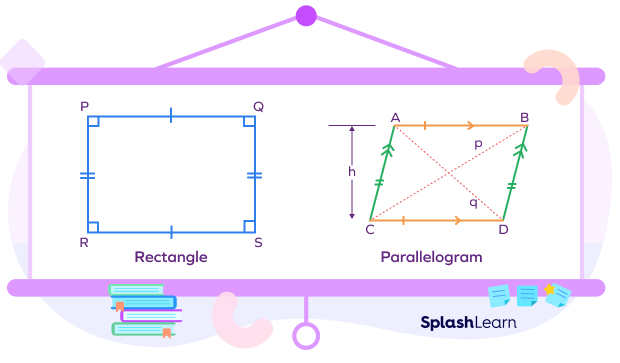
Recommended Games
What Is a Rectangle and a Parallelogram?
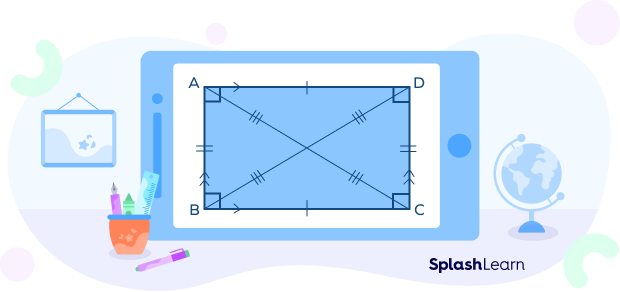
A rectangle is a closed 2D shape, having four sides, four corners, and four right angles $(90^\circ)$.
The opposite sides of a rectangle are equal and parallel. It is characterized by two dimensions, length, and width. Length is the longer side of the rectangle and width is the shorter side.
The line segments that join the opposite corners of a rectangle are called diagonals. The two diagonals of a rectangle bisect each other and are equal. Every angle of a rectangle measures 90°.
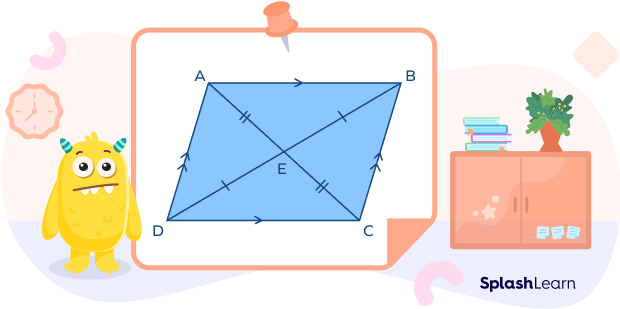
A parallelogram is a special type of quadrilateral in which opposite sides parallel and equal. Like all other quadrilaterals, the sum of all the angles of a parallelogram is 360°. Adjacent angles are supplementary. Four interior angles need not be right angles. Diagonals are not equal.
Recommended Worksheets
Properties of a Rectangle and a Parallelogram
Let’s discuss the properties of a rectangle and a parallelogram.
Properties of a Rectangle
- It is a flat and closed 2D shape.
- It has 4 sides, 4 angles, and 4 vertices.
- It has 2 dimensions, namely, length and width.
- Every angle of a rectangle is a right angle (measures $90^\circ$).
- Opposite sides are equal and parallel.
- Its two diagonals are equal in length.
- Diagonals of a rectangle bisect each other.
Properties of a Parallelogram
- In a parallelogram, the opposite sides are parallel and equal.
- The opposite angles of a parallelogram are equal.
- Like all other quadrilaterals, the sum of all the angles of a parallelogram is $360^\circ$.
- The adjacent angles of a parallelogram add up to $180^\circ$.
- The diagonals of a parallelogram bisect each other.
- The diagonals divide the parallelogram into two congruent triangles.
Difference between a Parallelogram and a Rectangle Chart
As mentioned earlier, a parallelogram and a rectangle are both quadrilaterals. The major distinction between them is that a rectangle is a type of a parallelogram, which has four $90^\circ$ angles, but the angles in a parallelogram need not be right angles. Diagonals of a rectangle are equal. Diagonals of a parallelogram are not equal.
Parallelogram vs Rectangle
| Parallelogram | Rectangle |
|---|---|
| A parallelogram is a quadrilateral. | A rectangle is a quadrilateral. It is a special case of parallelogram. |
| Opposite sides are parallel and equal. | Opposite sides are parallel and equal. |
| Two diagonals are not equal. | Two diagonals are of equal length. |
| Opposite angles are equal. | All angles are equal and measure 90. |
| A diagonal bisects a parallelogram into two congruent triangles. | Diagonals bisect rectangles to form two equal right-angled triangles. |
| Area of a parallelogram $=$ Base Height | Area of a rectangle $=$ Length Breadth |
| We can use the parallelogram law to find its sides. | We can use Pythagoras’ theorem to calculate its sides. |
Rectangle and Parallelogram Formulas
Once we know the lengths and sides of the diagonals of rectangle and parallelogram, we can use them to find the area and perimeter. The formulas for area and perimeter of rectangle and parallelogram are as follows:
- The formula for the area of a rectangle is:
Area of a rectangle $= l \times w$,
where “l” is the length of the rectangle and “w” is the width of the rectangle.
- The formula for the perimeter of a rectangle is:
Perimeter of a rectangle $= 2(l + w)$,
where “l” is the length of the rectangle and “w” is the width of the rectangle.
- The formula for the area of a parallelogram is:
Area of Parallelogram $= b \times h$,
where “b” is the length of the base of the parallelogram and “h” is the height of the parallelogram.
- The formula for the perimeter of a parallelogram is:
Perimeter of a parallelogram $= 2 (a + b)$,
where “a” and “b” are the adjacent sides of the parallelogram.
Facts about Difference between Rectangle and Parallelogram
- The word rectangle comes from medieval Latin rectangulum, which is a combination of rectus ‘straight’ and angulus ‘an angle’.
- The word “parallelogram” comes from the Greek word “parallelogrammon,” which is broken down as parallēlos ‘alongside another’ + grammē ‘line’.
- A rectangle is a special case of a parallelogram, in which each pair of adjacent sides are perpendicular.
- A parallelogram is a special case of a trapezium (known as a trapezoid in North America), in which both pairs of opposite sides are parallel and equal in length.
- A rectangle is cyclic, which means all corners can lie on a single circle.
- Rectangles, rhombuses, and squares are all parallelograms.
Conclusion
In this article, we have learned about the properties of rectangle and parallelogram, and the difference between them. It will help in understanding all the geometrical shapes related to a parallelogram and rectangle, and how to calculate the area and perimeter of both. Let us apply the knowledge to solve some examples.
Solved Examples on Difference between Rectangle and Parallelogram
1. Which of the following is not a parallelogram?
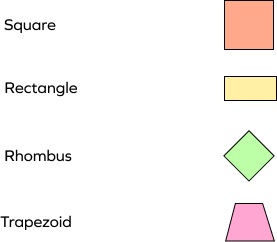
Solution:
A parallelogram has both the pair of opposite sides parallel and equal. Thus, square, rectangle, and rhombus are all parallelograms. Trapezium has only one pair of parallel sides and no equal sides. Thus, a trapezoid is not a parallelogram.
2. Find the area of a parallelogram, whose base is 10 inches and height is 5 inches.
Solution:
Base of the parallelogram (b) $= 10$ inches
Height of the parallelogram (h) $= 5$ inches
Area of the parallelogram (A) $= b \times h$
$= 10 \times 5$
$= 50\; inch^2$
The area of the parallelogram is $50\; inch^2$.
3. The perimeter of a parallelogram-shaped plot is 200 feet and one of its adjacent sides is 60 ft. Find the measure of its other adjacent side.
Solution:
The perimeter of parallelogram-shaped plot $= 200\; ft$
One adjacent side of the plot $= 60\; ft$
Let another adjacent side of the parallelogram-shaped plot be x.
Perimeter of a parallelogram $(P) = 2 (a + b)$, where “a” and “b” are the adjacent sides of the parallelogram.
$200 = 2 (60 + x)$
$100 = 60 + x$
$x = 100 \;-\; 60$
$x = 40\; ft$.
The measure of another adjacent side of the parallelogram-shaped plot is 40 ft.
4. The length of a rectangular TV screen is 24 inches. Its area is 360 sq.in. Find its width.
Solution:
Length of the tv screen $= 24$ inches
Area of the tv screen $=$
We know that,
Area of rectangle $= l \times w$
Thus, width $= \frac{Area}{Length}$
$w = \frac{360}{24}$
$w = 15$ inches.
The width of the rectangular tv screen is 15 inches.
5. The length and width of a rectangular wall are 80 ft. and 20 ft., respectively. Find the cost of painting the wall if the rate of painting is 1.5 dollars per sq. ft.
Solution:
Length of the wall $= 80\;ft$
Width of the wall $= 20\;ft$
We know that,
Area of the rectangle $= l \times w$
Area of the wall $= 80 \times 20$
$= 1600\;sq. \;ft$
1 sq. ft of painting costs 1.5 dollars.
Thus, for 1600 sq. ft , the cost of painting the wall will be, $1600 \times 1.5 = 2400$ dollars.
Practice Problems on Difference between Rectangle and Parallelogram
Difference Between Rectangle and Parallelogram: Chart & Examples
The diagonals of a ________ are equal in length.
A rectangle has two diagonals that are of equal length.
What type of quadrilateral has all angles measuring 90° and opposite sides equal?
A rectangle has all angles measuring $90^\circ$ and opposite sides measuring equal.
In the following image, $\angle Y = 40^\circ$. The measure of $\angle W$ is _____.
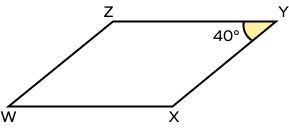
Opposite angles of a parallelogram are equal. As $\angle Y$ and $\angle W$ are opposite angles of a parallelogram, they are equal. Thus, if $\angle Y = 40^\circ$, then $\angle W = 40^\circ$.
The area of a rectangle with length 8 in and width 5 in is ________.
Area of a rectangle $= l \times w$,
where “l” is the length of the rectangle and “w” is the width of the rectangle.
Thus, $A = 8\times5 = 40\;inch^2$.
The perimeter of the given parallelogram is ________.
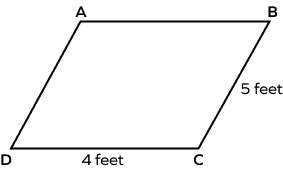
Perimeter of a parallelogram $= 2\;(a\;+\;b)$,
where “a” and “b” are the adjacent sides of the parallelogram.
Thus, $P = 2\;(4\;+\;5)$
$= 2 (9) = 18\;feet$
Frequently Asked Questions on the Difference between Rectangle and Parallelogram
Is a parallelogram a rectangle?
A parallelogram is not always a rectangle. A rectangle is always a parallelogram. Parallelogram has opposite sides equal and parallel. Rectangle also has opposite sides equal and parallel. The difference between the two is that all interior angles of a rectangle are $90^\circ$ while angles of of parallelogram need not be $90^\circ$. So, a rectangle can be called a parallelogram because it fulfills all the requirements of a parallelogram.
Is a rectangle a parallelogram ?
Yes, a rectangle is a special case of parallelogram. In fact, all rectangles are parallelograms because a rectangle has two sets opposite sides that are equal and parallel. Therefore, it possesses all the properties of a parallelogram.
How are rectangles and parallelograms different in terms of the diagonals?
A rectangle has two diagonals that are of equal length, while a parallelogram has two diagonals that are not of equal length. Also, diagonals bisect rectangles to form two equal right angled triangles and diagonals of parallelogram bisect parallelograms into two non-right congruent triangles.
Is it necessary that all sides be equal in a quadrilateral to be a parallelogram?
No, a parallelogram does not have all sides equal. Only opposite sides of a parallelogram are equal. Also, if all sides are equal, it is said to be a square.




































