Direct Variation: Definition, Formula, Equation, Examples, FAQs

What Is Direct Variation in Math?

Direct variation is a type of proportionality in which one quantity directly varies with respect to a change in another quantity, by the same factor. 

This means that an increase in one quantity results in a proportionate increase in the other quantity. Similarly, a decrease in one quantity results in a proportionate decrease in the other quantity. There will be a proportionate increase or decrease.

Note that the ratio between two quantities that are in direct proportion or direct variation always remains the same. 

In direct variation, the variable that represents the cause of the relationship is called the independent variable, generally denoted by x. The other variable depends on the value of the independent variable; it is called the dependent variable, generally denoted by y. 

(Note: It’s important to note that the roles of independent and dependent variables vary depending on the specific context and the relationship between the defined variables. It is always better to first understand the relationship between two quantities in comparison.)

Direct variation real-life example:

Suppose you are working on an hourly pay basis. In this case, the number of hours you work is directly proportional to your earnings. The more you work, the more you earn. You can earn double by working twice as many hours.  

Here, $x =$ Number of hours you work and $y =$ The amount of money you earn

Direct Variation Definition

Direct variation or direct proportionality is a mathematical relationship between two variables where one variable varies in direct proportion with respect to the other variable.

Direct Variation Symbol

Suppose that a variable y is directly proportional to x. In other words, y varies directly as x.

We can write this mathematically as

$y \propto x$

Symbol “$\propto$” stands for “is proportional to.”

What Is a Direct Variation Equation? (Direct Variation Formula)

The relationship between two variables x and y, which are in direct variation, can be represented by an equation

$y = kx$

where

$k = \frac{y}{x}$ is the constant of variation representing the constant ratio between the two variables.

Here, k is a non-zero real constant. The value of k can be both positive or negative.

The above equation can be decoded as “y varies directly with x” or “y varies directly as x.” The equation can be used to derive different formulas according to the requirements of a solution. 

Different forms of the direct variation formula are as follows:

• To solve for the constant of variation, k, we can shuffle the formula.

$k = \frac{y}{x}$ and $x \neq 0$

• To solve for one of the variables (x or y), we can shuffle the formula.

$y = kx$

or

$x = \frac{y}{k}$

Direct Variation on a Graph

Note that the graph of the direct variation linear equation $y = kx$ is a straight line passing through the origin.

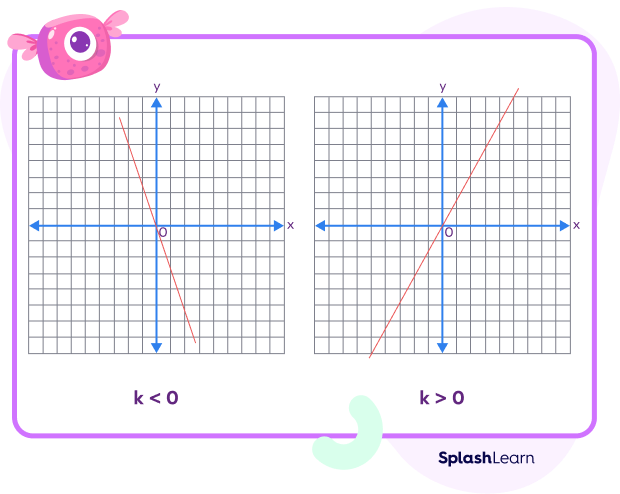
• If k is positive, then the line will rise from left to right, passing through the origin.
• If k is negative, then the line will fall from left to right, passing through the origin.

The slope of the line represents the constant of variation in a direct variation. It indicates how much the dependent variable changes for each unit increase in the independent variable.

So, to understand how to graph direct variation, we will identify the plot points satisfying the equation $y = kx$.

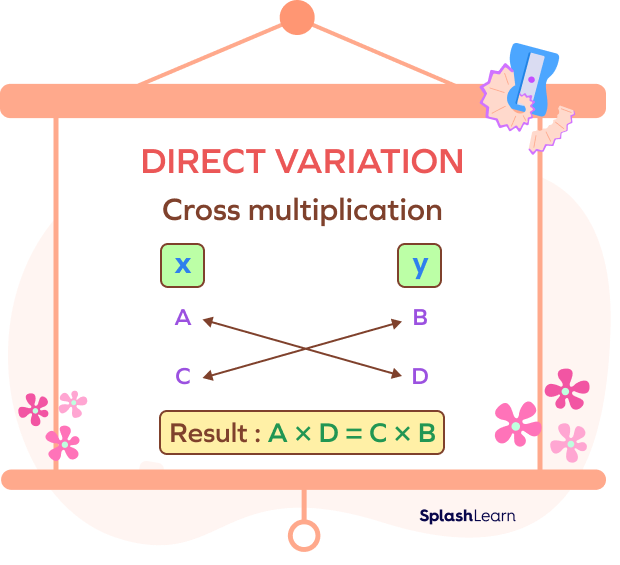
Cross Multiplication Method to Solve Direct Variation Problems

We can easily solve direct variation problems using the cross multiplication method. Consider two variables, x and y, in direct variation. 

Let y = B for x = A.

Let y = D for x = C.

Since x and y are in direct variation, we can write the proportion as

$\frac{A}{B} = \frac{C}{D}$ 

By cross multiplication, we get

Thus, $A \times D = B \times C$

We can find any missing value using this method.

Difference between Direct Variation and Inverse Variation

In a direct variation, the variables change in proportion to each other, while in an inverse variation, the variables change in inverse proportion to each other.

See this comparison table that shows the difference between Direct and Inverse variations:

Feature	Direct Variation	Inverse Variation
Definition	One variable varies in direct proportion with respect to the other variable.	One variable varies in inverse proportion with respect to the other variable
Meaning	As x increases, y increases by the same factor. As x decreases, y decreases by the same factor.	As x increases, y decreases by the same factor. As x decreases, y increases by the same factor.
Equation	$y = kx$	$y = \frac{k}{x}$
Symbol	$x \propto y$ x “is directly proportional to” y.	$x \propto \frac{1}{y}$ x “is inversely proportional to” y.
Constant of Variation	$k = \frac{y}{x}$	$k = xy$
Graph	The graph is a straight line that passes through the origin.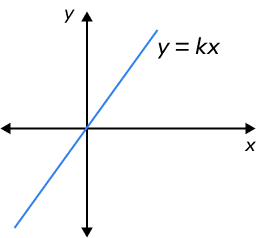	The plot is a hyperbola with two branches.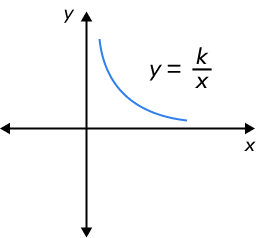
Examples	The cost of items is directly proportional to the number of items.	The speed of an object is inversely proportional to the time taken.

Facts on Direct Variation

Conclusion

Okay, so we now have a clear idea of the concepts relating to direct variation, including direct variation function, definition, graph, differences, and much more. Let us now look at some examples and practice problems to boost our understanding of the concept.

Solved Examples of Direct Variation

1. The cost of printing 100 pages is $50. What will be the cost of printing 150 pages?

Solution:

Cost $\propto$ Number of pages

Cost $= k \times$ Number of pages

$k = \frac{y}{x} = \frac{cost}{Number \;of \;pages}$

$k = \frac{50}{100} = 0.5$

Now, the cost of 150 pages can be calculated by a direct variation equation.

Cost $= 0.5 \times $Number of pages

Cost $= 0.5 \times 150$

Cost $= 75$

Therefore, $\$75$ is the cost of printing 150 pages.

Another method:

Cost	Number of pages
$\$50$	100
?	150

By cross multiplication, we get

$\$50 \times 150 = 100 \times$ ?

?$ = \frac{\$7500}{100}$

? $= \$75$

2. If the number and cost of notebooks have a direct variation, what will be the cost of 15 notebooks if 5 notebooks cost $\$10$?

Solution:

As the cost varies directly with the number of notebooks, we can solve it by setting up the proportions.

5 notebooks cost $\$10$.

Let the cost of 15 notebooks to be x.

The proportion can be written as

$\frac{5}{10} = \frac{15}{x}$

Cross multiply.

$5 \times x = 10 \times 15$

Solve for x

$x = 30$

Therefore, $\$30$ is the cost of 15 notebooks.

3. If a car covers 240 miles in 4 hours time. How many miles will it travel in 6 hours?

Solution: 

We know that the distance covered is directly proportional to the time taken. So, we can solve this question accordingly.

Distance covered	Time taken
240 miles	4 hours
?	6 hours

By cross multiplication, we get

240 miles$\times 6 =$ ?$\times 4$ hours

?$= 360$ miles

Therefore, the car will cover 360 miles in 6 hours.

4. A company produces 100 units of a product per day. How many units will it produce in 5 days?

Solution:

The number of units produced are directly proportional to the number of days.

Number of units produced	Number of days
100	1
y = ?	5

Suppose that the company produces y units in 5 days.

By cross multiplication, we get

$y = 100 \times 5$

$y = 500$

Therefore, 500 units can be produced in 5 days.

5. Find the constant of direct variation where the cost of 4 dozen oranges is $\$24$. Also, find the cost of 8 dozen oranges.

Solution:

Assume the cost of 8 dozen oranges to be y. 

As we can see that the cost of oranges varies directly with the number of dozens. So, we can set up a proportion as

$\frac{4}{24} = 8y$

Isolate y on one side by cross-multiplying both sides

$4y = 24 \times 8$

Simplify it

$4y = 192$

$y = 48$

Therefore, 8 dozen oranges will cost $48.

Now, let us find the constant of direct variation by using the equation y = kx

where 

y = the cost,

x = the number of dozens, and

k = the constant of variation

$k = \frac{1}{6}$

Therefore, $\frac{1}{6}$ or 0.1667 (approx) is the constant of direct variation.

Practice Problems on Direct Variation

Frequently Asked Questions about Direct Variation