What Is Quotative Division?
Quotative division is a division problem in which we divide a given number into groups of a measured quantity, and the goal is to find the number of groups.
Division means breaking a number or a group into equal parts. There are two ways in which we can categorize division—partitive division and quotative division.
In the partitive division, we equally distribute or share a quantity into a number of groups, and our goal is to determine how many objects each (equal) group can receive.
In the quotative approach to division, we know the number of items assigned for each group and we find the number of groups. Let’s dive in and learn more about this type of division.
Quotative Division Definition
Quotative division is a process of splitting a set of items or a number into groups of a measured quantity. In this division, we know the number of objects each group should receive, and we aim to find out how many such (equal) groups we can create.
Let us consider an example to understand the quotative method of division. Suppose you wish to divide 8 goldfish into jars, with 2 fish in each. How many jars will you need?
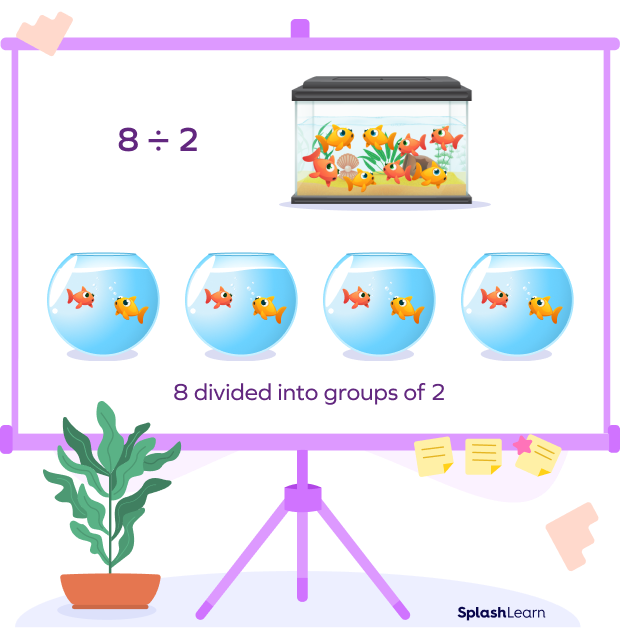
It’s a quotative division model since the group’s size is known. Here we need to divide 8 into groups of $2, 8 \div 2 = 4$, which gives a result of 4 groups. So, we need 4 jars.
Recommended Games
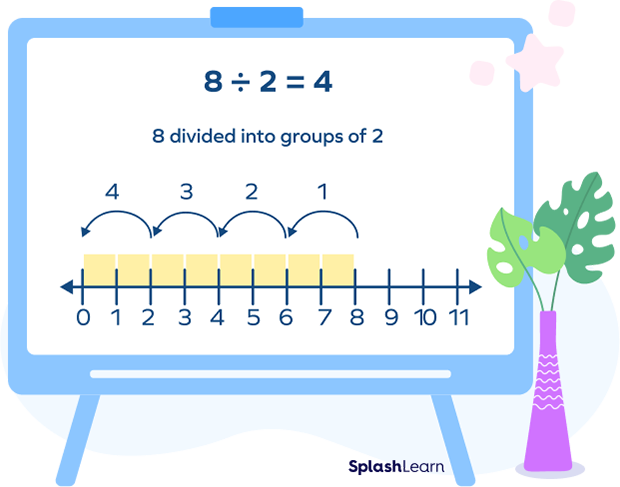
Understanding Quotative Division Using Number Line
Let’s conceptualize the quotative model of division linearly on a number line. To divide 8 objects into groups of 2, we can consider using repeated subtraction to take away groups of 2 until all are removed (or till we reach zero).
Recommended Worksheets
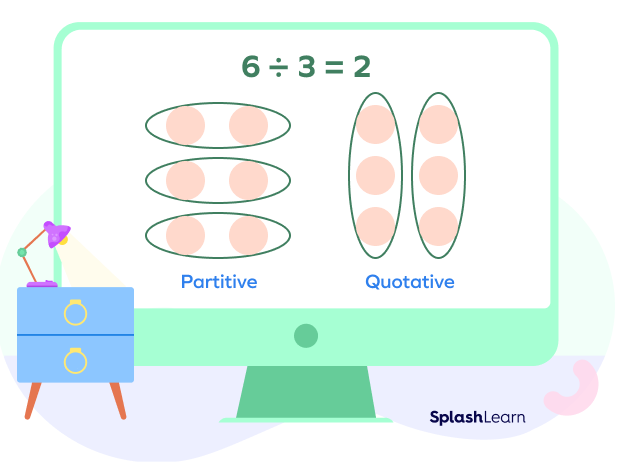
What Is the Difference Between Partitive and Quotative Division?
In both division types, we need to divide a number by another whole number. The difference between partitive and quotative division boils down to what the result represents.
| Quotative Division | Partitive Division |
| In the quotative division problem, we know the number of items assigned to each group and we find the number of groups. | In the partitive division problem, we know the total number of groups, and we have to find the number of items in each group. |
| The number of items in each group is known. | Total number of groups is known. |
| We have to find the number of groups. | We have to find the number of items in each group. |
| Example: Dividing 10 in equal groups of 2. | Example: Dividing 10 items equally into 5 groups. |
In the case of the partitive model of division, the result represents the number of shared objects in each group. On the contrary, in the quotative model of division, the answer represents the number of groups within the shared quantity. Although the result will be the same number, conceptualizing how the division takes place for each type is different.
How to Teach Quotative Division
Role-playing: A great way to help kids understand quotative division is through role-playing. If you have a group of students struggling with quotative division, set up a situation where they all work together in a store. Then, tell them they need to pack some orders into boxes of known measure.
Flashcards: Use flashcards by talking about examples of quotative division in everyday life.
Worksheets: Create worksheets that are available online or handmade to help students practice quotative division.
Conclusion
Learning quotative division is easy once you learn all the basics. Let’s solve a few quotative division examples and practice problems.
Solved Examples of Quotative Division
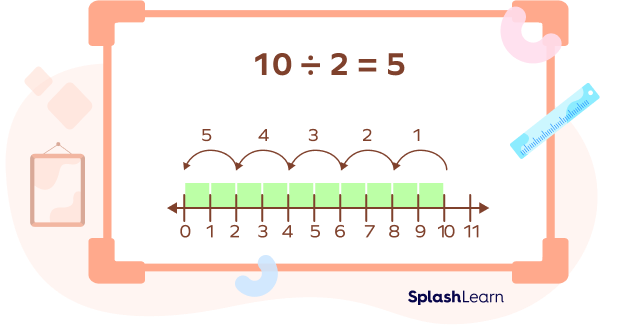
- Divide 10 into groups of 2 on a number line.
- If John has 12 cookies and packs them in boxes of 4 each. What type of division will it be?
Solution:
To determine whether the division is partitive or quotative, we need to find what we already know and what we need to find.
We know the number of items in each group.
We need to find the total number of groups. To find the total number of groups, we use quotative division.
- If there are twenty students in a class and the teacher has to create groups of 5 to make quiz teams, how many groups will there be?
Solution:
If there are a total of 20 students in school and the teacher needs to create groups of 5, we should divide 20 by 5.
$20 \div 5 = 4$
This means there will be a total of 4 teams.
Practice Problems on Quotative Division
Quotative Division – Definition with Examples
Eric is selling pizzas for $\$3$ each. Stella has $\$18$, so how many pizzas can she buy with her money?
The price of each pizza is $\$3$. Stella has a total $\$18$. So, she can buy $18 \div 3$, which is equal to 6 pizzas.
A teacher divides her students into groups of 3 each. There are 15 students in her class. How many groups can she make?
We need to divide 15 into groups of 3. We can make $15 \div 3$, which is equal to 5 groups.
Dylan has 50 candies. If he packs them in bags of 6 each. How many candies will he be left unpacked?
On dividing 50 candies by 6, he can pack 48 candies into 8 packs and will be left with $50 \;–\; 48$ or 2 candies.
Frequently Asked Questions on Quotative Division
How is 8 divided into 2 groups different from 8 divided into groups of 2?
Solution:
In both cases, we are dividing 8 by 2. Even though it results in the same number, we need to understand how the division takes place for each case. When we divide 8 into 2 groups, we pose a situation where we share 8 equally among 2 groups. This is a partitive model of division.
When we divide 8 into groups of 2, it involves repeated measuring out. Since we know the group size, this is quotative division.
What does the remainder represent in the partitive division?
Solution:
The remainder is the portion of the number that is to be divided (dividend) that cannot be fairly divided by the divisor.
What does the quotient represent in the partitive division?
Solution:
The quotient is the result obtained by dividing a number by another. In the partitive division, the quotient represents the number of shared objects in each group.




































