Decompose Fractions – Introduction
“Decompose” means to separate or break something apart. We can decompose numbers as well as geometric shapes. Decomposing numbers involves breaking a larger number into smaller numbers.
For example, consider breaking the number 10 into parts. We can decompose ten into five, three, and two. Alternatively, we can compose the number ten by putting together five, four, and one. There is often more than one way to decompose a number.
We all know that fractions are part of a whole. But just like whole numbers, we can compose and decompose fractions. Does that sound interesting? Let’s dive in and learn more about decomposing fractions.
Recommended Games
What Is Decomposing Fractions?
A fraction represents a part of a whole.
To decompose a fraction means breaking it into smaller parts.
Combining or adding all the smaller or decomposed parts must result in the initial fraction.
For instance, the fraction $\frac{3}{4}$ means we have three out of four equal parts. We can split this fraction into even smaller parts!
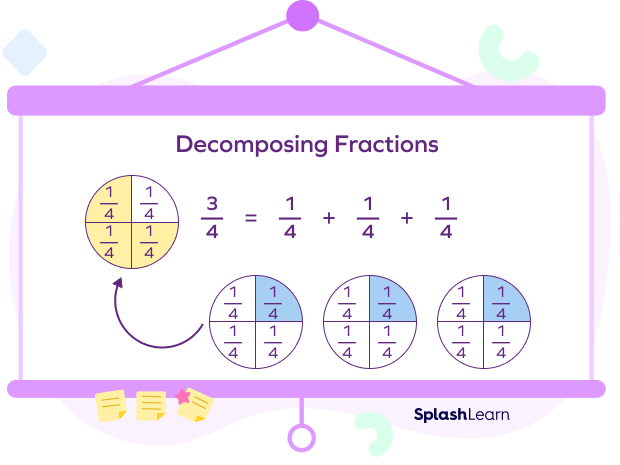
We can decompose the fraction $\frac{3}{4}$ into three one-fourths. When we add these parts together, we get the fraction $\frac{3}{4}$.
What happens when we decompose a fraction into a sum of smaller fractions? We break the numerator into parts. Unlike partitioning, where we usually consider the fractional concept of dividing shapes into equal parts, decomposing does not need to be of equivalent size.
Let’s look at other decompositions of $\frac{3}{4}$.
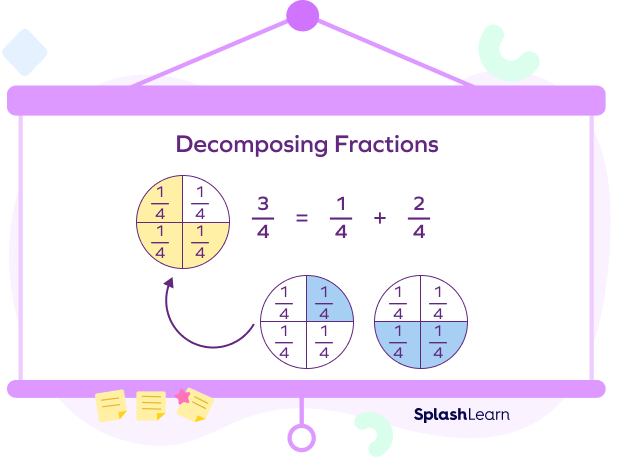
$\frac{3}{4} = \frac{1}{4} + \frac{2}{4}$
Recommended Worksheets
How to Decompose Fractions?
Decomposition of fractions can be done in two ways: unit fractions or non-unit fractions.
How to Decompose Fractions into Unit Fractions?
A fraction with one as a numerator is called a unit fraction. When a whole is divided into equal parts, the unit fraction represents one part of the whole—for example, $\frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}$, etc.
The most basic way to decompose a fraction is to break it into unit fractions.
For example,
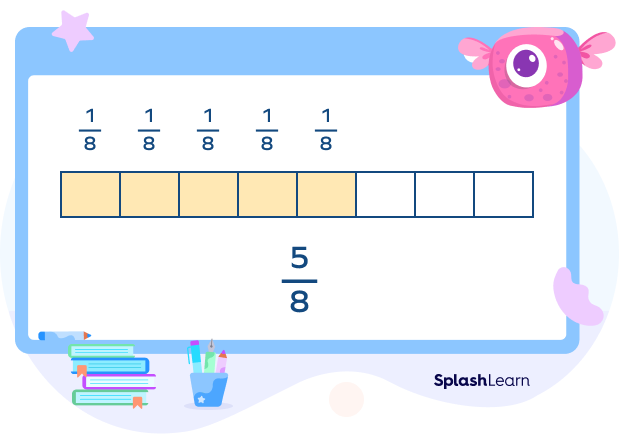
We can see that $\frac{5}{8}$ is the same as the five times the unit fraction $\frac{1}{8}$.
$\frac{5}{8} = \frac{1}{8} + \frac{1}{8} + \frac{1}{8} + \frac{1}{8} + \frac{1}{8}$
When you break a fraction into unit fractions, you split it into equal parts.
Let’s take another example. Consider the fraction $\frac{9}{5}$. We can divide the fraction as shown below.
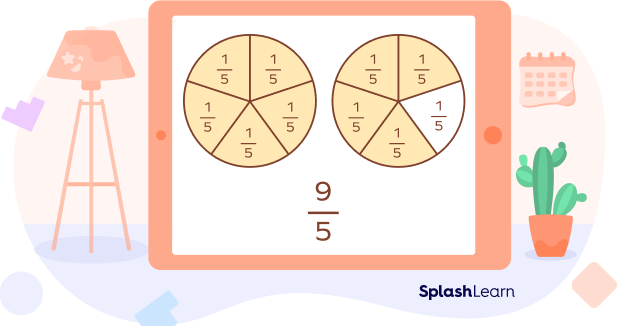
$\frac{9}{5} = \frac{1}{5} + \frac{1}{5} + \frac{1}{5} + \frac{1}{5} + \frac{1}{5} + \frac{1}{5} + \frac{1}{5} + \frac{1}{5} + \frac{1}{5}$
How to Decompose Fractions into Non-Unit Fractions?
In this method, we decompose a fraction into different smaller like fractions. We can express a fraction as the sum of smaller fractions, which are not all unit fractions. Adding up all the decomposed fractions must result in the initial fraction.
For example, in the figure below, $\frac{7}{9}$ of the circle is divided into four unequal parts.

$\frac{7}{9} = \frac{3}{9} + \frac{1}{9} + \frac{1}{9} + \frac{2}{9}$.
Let’s take another example: How do we decompose $\frac{12}{5}$?
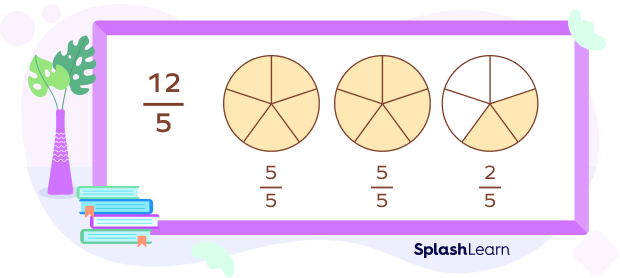
We can break it down into $\frac{5}{5} + \frac{5}{5} + \frac{2}{5} = 1 + 1 + \frac{2}{5} = 2\frac{2}{5}$
This gives us the mixed number form of the fraction $\frac{12}{5}$.
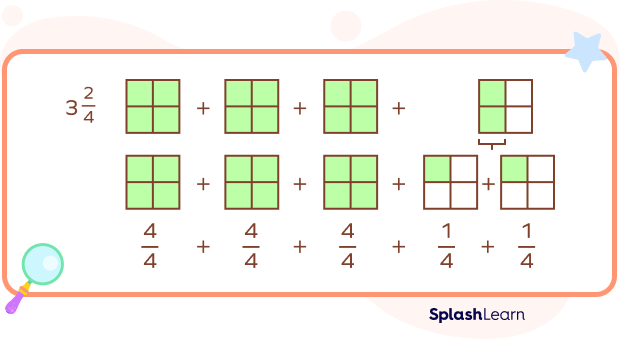
How to Decompose Mixed Numbers?
A mixed fraction is a combination of a whole number and a proper fraction, a number between two consecutive whole numbers.
For example, $1\frac{3}{4}$ is a mixed number between the whole numbers 1 and 2.
Now, let’s understand how to decompose a mixed number.
Conclusion
Practicing how to decompose fractions can help children perform various operations with fractions. It will improve their simplifying skills and teach them different techniques to master concepts and work on fractions.
Solved Examples
1. Decompose the fraction $\frac{4}{7}$ into unit fractions.
Solution: To decompose 47 into unit fractions, we can split the numerator four and express the fraction as the sum of 4 one-sevenths.
$\frac{4}{7} = \frac{1}{7} + \frac{1}{7} + \frac{1}{7} + \frac{1}{7}$
2. Write the given fraction as the sum of two different fractions: $\frac{3}{10}$.
Solution: To express the fraction as the sum of two different fractions, we can decompose the numerator three into 1 and 2.
So, $\frac{3}{10} = \frac{1}{10} + \frac{2}{10}$
3. Write the fraction $\frac{6}{11}$ as the sum of three equal fractions.
Solution: To express the given fraction as the sum of three equal fractions, we can split the numerator six into three equal parts. $6 = 2 + 2 + 2$
So, $\frac{6}{11} = \frac{2}{11} + \frac{2}{11} + \frac{2}{11}$
4. Decompose the improper fraction $\frac{7}{4}$ and write the mixed number form of the fraction.
Solution: To break down the improper fraction, we can split the numerator as follows:
$\frac{7}{4} = \frac{4}{4} + \frac{3}{4} = 1 + \frac{3}{4}= 1\frac{3}{4}$
Practice Problems
Decompose Fractions
Which of the following sum equals $\frac{1}{2}$?
$\frac{1}{4} + \frac{1}{4} = \frac{2}{4} = \frac{1}{2}$
Select a fraction to complete the equation $\frac{2}{8} + \frac{3}{8} + \frac{1}{8} + \underline{} = \frac{10}{8}$
Since $2 + 3 + 1 + 4 = 10, \frac{2}{8} + \frac{3}{8} + \frac{1}{8} + \frac{4}{8} = \frac{10}{8}$
Which expression matches the model shown below?

The whole is divided into 12 equal parts. Blue parts represent $\frac{4}{12}$ of the whole; the yellow part represents $\frac{1}{12}$, and the pink parts represent $\frac{5}{12}$.
Which of the following is equivalent to $\frac{1}{6} + \frac{2}{6} + \frac{2}{6}$?




$\frac{1}{6} + \frac{2}{6} + \frac{2}{6} = \frac{5}{6}$

Select an expression that is more than $\frac{8}{11}$.
The sum of $\frac{2}{11} + \frac{3}{11} + \frac{5}{11}$ is $\frac{10}{11}$, greater than $\frac{8}{11}$ .
Frequently Asked Questions
Can we decompose fractions using operations other than addition?
No, when we decompose a fraction, we write it as the sum of smaller fractions. To decompose a fraction means breaking it into smaller parts. Combining all the decomposed parts must result in the initial fraction.
Can we decompose a unit fraction?
To decompose a unit fraction, we can decompose the fraction equivalent to a unit fraction. For example, $\frac{1}{3}$ is a unit fraction. $\frac{1}{3}$ is equal to $\frac{2}{6}$, so we can write it as $\frac{2}{6}$.
$\frac{2}{6} = \frac{1}{6} + \frac{1}{6}$
Therefore, $\frac{1}{3} = \frac{1}{6} + \frac{1}{6}$
Can we decompose fractions into their equivalent fractions?
Equivalent fractions have different numerators and denominators but are equal to the same value. Decomposing a fraction means writing it as the sum of smaller fractions. Since equivalent fractions are of equal value, we cannot decompose a fraction into an equivalent fraction. For example, $\frac{3}{6}$ cannot be decomposed into $\frac{1}{2}$ because $\frac{3}{6} = \frac{1}{2}$.




































