Factor
Factors are the numbers that are multiplied together to obtain a product.
For example: The product of 6 × 7 = 42. It means that the numbers 6 and 7 are factors of 42.
Recommended Games
What are Factor Pairs?
In math, a factor pair is defined as a set of two factors, which, when multiplied together, give a particular product. In other words, it is a set of two numbers we multiply to get a product.
For instance, in the multiplication statement, 6 × 7 = 42, 6 and 7 is one of the factor pair that gives us the product 42.
In other words, 42 is the product of 6 and 7.
A number can have multiple factor pairs. We can write the factor pair as (a, b) where a and b are the factors of the number.
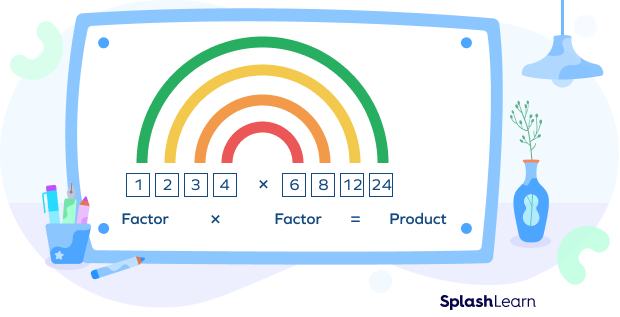
For example: For the number 24;
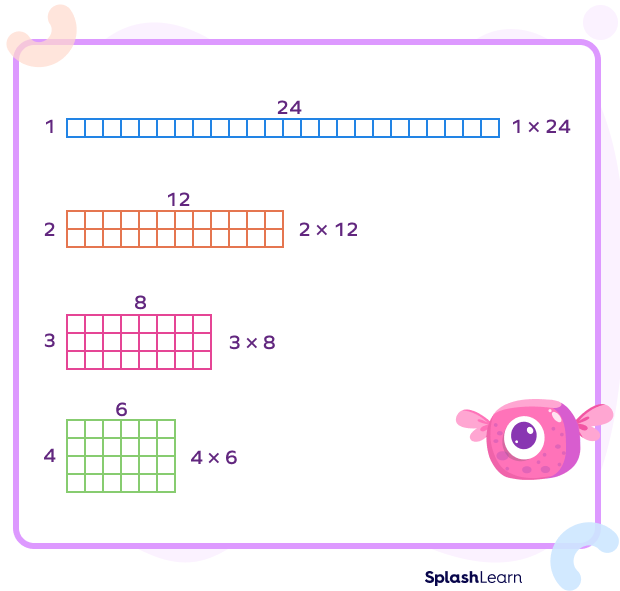
Factors of 24 are 1, 2, 3, 4, 6, 8, 12 and 24
We can write 24 as the product of 1 × 24; 2 × 12 ; 3 × 8; 4 × 6
So, the factor pairs of 24 are (1, 24); (2, 12); (3, 8) and (4, 6).
Negative Factor Pairs:
We can also find negative factor pairs of a number since the product of two negative integers is always positive. For example, the negative factor pairs of 24 are (-1, -24); (-2, -12); (-3, -8) and (-4, -6).
Recommended Worksheets
Factor Pairs of Integers
An integer is a whole number(not in fractional form) that can be positive, negative or 0.
For example: -3, -10, 0, 18 etc.
- Positive Integers
Factor pairs of positive integers are the pairs of integers whose product will be the integer.
For example: Factors of 12 are 1, 2, 3, 4, 6, and 12.
We can write 12 = 1 × 12; 2 × 6; 3 × 4
So, the factor of 12 in pairs = (1, 12); (2, 6); (3, 4)
- Negative Integers
Negative numbers are the numbers that lie on the left side of 0. For example: -2, -10, -150.
When we talk about the factor pairs of such numbers, we need to see the sign of the number. Since, the negative numbers have minus(-) sign in front of them, so one factor in the factor pair will be a negative number.
For example: Find the factor pairs of -24.
Factors of -24 are 1, 2, 3, 4, 6, 8, 12, 24, -1, -2, -3, -4, -6, -8, -12, and -24.
We can write -24 = 1 × -24, 2 × -12, 3 × -8, 4 × -6, 6 × -4, 8 × -3, 12 × -2, and 24 × -1.
The factor pairs of -24 are (1, -24); (2, -12); (3, -8); (4, -6); (6, -4); (8, -3); (12, -2); (24, -1).
- Prime Numbers
Prime Number is a number that has only two factors, 1 and the number itself.
Any prime number will have only a single factor pair since there are only two factors. For Example: For the prime number 13: 13 × 1 = 13, therefore it has only one factor pair. In this case the factor pair will be (1, 13) only.
Factor Pairs of Fractions
Fractions are the numbers that can be represented in the form of $\frac{p}{q}$ where p is the numerator and q is the denominator. For example: $\frac{3}{5}$, $\frac{11}{15}$ etc.
Finding the factors of the fractions is the same as finding the factors of a whole number.
For example: In the fraction $\frac{3}{5}$, factors of 3 are 1, 3 and factors of 5 are 1, 5.
So, the factors of $\frac{3}{5}$ are 1, 3,$ \frac{1}{5}$, $\frac{3}{5}$.
So, the factor pairs of $\frac{3}{5}$ are (1, $\frac{3}{5})$; (3, $\frac{1}{5}$).
Factor Pairs of Decimal Number
A decimal number is a number whose whole number part and the fractional part is separated by a decimal point. For example: 1.2, 3.456, 5.28 etc
For example: For the decimal 1.2.
Factors of 1.2 are 1, 2, 3, 4, 6, 12, 0.1, 0.2, 0.3, 0.4, 0.6, 1.2.
The factor pairs of 1.2 are (1, 1.2); (2, 0.6); (3, 0.4); (4, 0.3); (6, 0.2); (12, 0.1).
Factor Pairs of Algebraic Expressions
An algebraic expression is an expression that is made up of variables and constants along with the algebraic operations like addition, subtraction etc.
The factors of an algebraic expression can be formed by either splitting the middle term or finding the HCF.
Example 1: For the expression 2 x + 6
2 x + 6 = 2 (x + 3)
Factors of 2 x + 6 are 1, 2, (x + 3), (2 x + 6).
So, the factor pairs of 2 x + 6 are (1, (2 x + 6)) and (2, (x + 3)).
Example 2: For the expression $x^ 2$ – x-2.
$x^2$ – x – 2 = $x^2$ – 2 x + x – 2 = x (x – 2) + 1(x – 2) = (x + 1) (x – 2)
Factors of $x^ 2$ – x – 2 are 1, (x + 1), (x – 2) and ($x^2$ – x – 2)
So, the factor pairs of $x^2$ – x – 2 are (1, ($x^2$ – x – 2)); ((x + 1),(x – 2)).
Conclusion
In this article, we learnt about factor pairs. The pair of two factors which gives the product is known as factor pair. To read more such informative articles on other concepts, do visit our website. We, at SplashLearn, are on a mission to make learning fun and interactive for all students.
Solved Examples
1. Find the factor pairs of the whole number 25?
Answer: The factors of 25 are 1, 5 and 25.
The factor pairs of 25 are (1, 25) and (5, 5).
2. How many factor pairs can you find for the number 35?
Answer: Factors of 35 are 1, 5, 7 and 35.
The factor pairs of 35 are (1, 35) and (5, 7).
So, there are two factor pairs for the number 35.
3. What are the factor pairs of 2.45?
Answer: The factors of 2.45 are 1, 5, 7, 0.1, 0.5, 0.7, 0.35, 0.01, 0.05, 0.07, 0.35, 0.49, 4.9, 24.5, 2.45 and 245.
1, 5, 7, 35, 49, 245, 0.1, 0.5, 0.7, 3.5, 4.9, 2.45, 0.01, 0.05, 0.07, 0.35, 0.49, and 2.45
The factor pairs of 2.45 are (1, 2.45), (5, 0.49), (7, 0.35), (35, 0.07), (49, 0.05), (245, 0.01), (0.1, 2.45), (0.5, 4.9), and (0.7, 3.5).
Practice Problems
Factor Pairs
How many factor pair(s) are there for a prime number?
A prime number has only two factors i.e. one and itself. So, there is only one factor pair of a prime number.
Which one of the following is a factor pair for $\frac{4}{11}$?
2 ✕ $\frac{2}{11}$ = $\frac{4}{11}$. So, (2, $\frac{2}{11}$) is a factor pair of $\frac{4}{11}$.
Which one of the following is a factor pair for x$^{2}$ - 5x + 6?
x$^{2}$ - 5x + 6 = x$^{2}$ - 2x - 3x + 6 = x(x-2)-3(x-2) = (x-3)(x-2)
Factors of x$^{2}$ - 5x + 6 are 1, (x-3),(x-2) and (x$^{2}$ - 5x + 6)
So, ((x-3),(x-2)) is a factor pair of x$^{2}$ - 5x + 6.
Frequently Asked Questions
What is the difference between factors and factor pairs?
A number or algebraic expression that divides the another number or expression evenly is known as a factor. For example: Factors of 6 are 1, 2, 3 and 6
On the other hand, a factor pair is the pair of the factors which when multiplied together gives the product. For example: Factor pairs of 6 are (1, 6) and (2, 3).
What are the minimum factor pair(s) of a composite whole number?
The minimum factor pairs of a composite whole number are 2.
Which numbers have only one factor pair?
Prime numbers have only one factor pair.




































