Axis: Introduction
The plural of axis is axes. An axis is a fixed reference line around which figures are drawn, and which is used for plotting the coordinates. In a coordinate system, the horizontal axis is known as the x-axis, and the vertical axis is known as the y-axis. The plural of axis, axes, refers to the “x” and ”y” axes that intersect each other at a right angle on a graph.
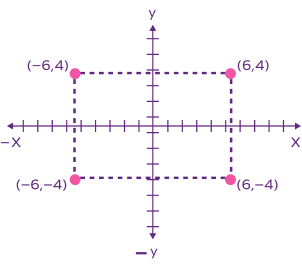
Look at the image below to understand the x-axis and y-axis.
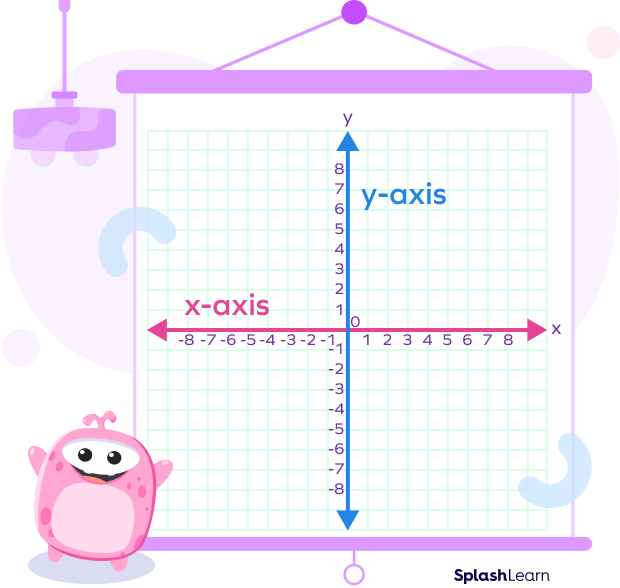
What Is the Plural of Axis?
The plural form of axis is axes. It is the collective term used to describe the horizontal line (x-axis) and vertical line (y-axis) on a coordinate plane. Axes (plural of axis) are the lines that help measure data on a graph’s grid lines.
Definition of Axis
Axis refers to one axis, and to talk about x-axis and y-axis we use the plural form “axes.” We now know that axes is the plural of axis. According to the axis definition in math, we refer to an axis as the lines that can be used to measure different coordinates on a graph or a grid.
The definition of axes is self-sufficient in understanding the meaning of different axes and their purpose on the Cartesian plane.
The Vertical Axis and the Horizontal Axis
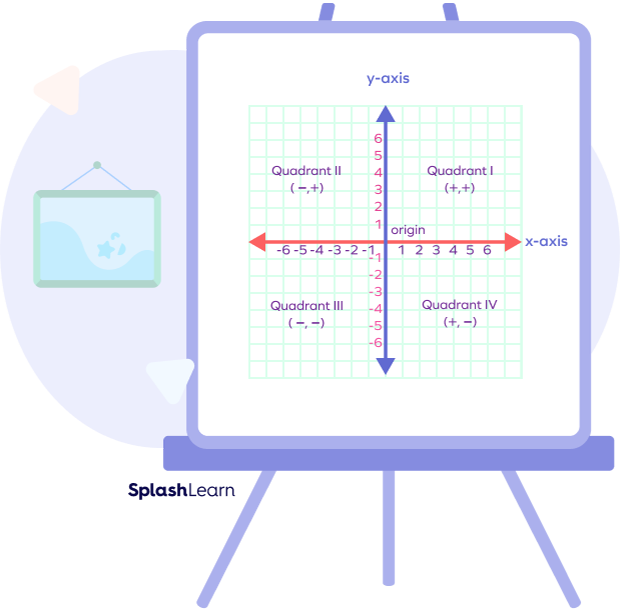
When we draw axes (plural of axis) on graph paper, we draw one vertical axis and one horizontal axis.
We call the vertical axis the y-axis, whereas the horizontal axis is the x-axis. Both the x-axis and the y-axis meet each other at a point, which is called the origin.
On a graph, the two axes (plural of axis), the x-axis and y-axis, can be plotted with the help of a ruler. Only occasionally can we also use the z-axis, in which case, the coordinates are depicted as (x, y, z).
Coordinate Point
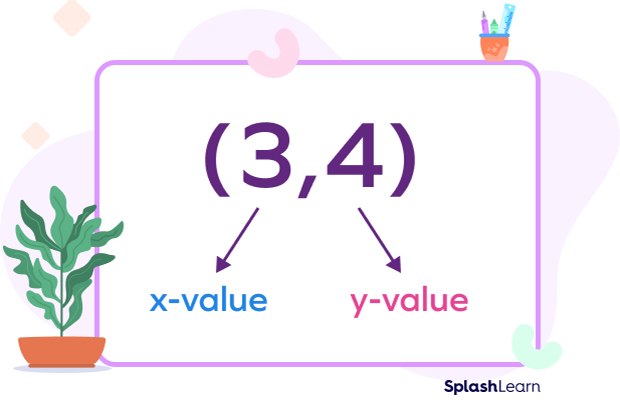
Using the x-axis and the y-axis, we can locate any given coordinate point. A coordinate point is like a dot on the Cartesian Coordinate plane. Every coordinate is designated using both axes (plural of axis).
The x value will tell us the location of the coordinate on the x-axis, and the y value will tell us the location of the coordinate on the y-axis. A coordinate point is written in brackets, with a comma separating the two values. The x-axis value is written first, followed by the value of the y-axis.
Another traditional definition of an axis in math is a line used as a reference to represent a position, rotation, or symmetry.
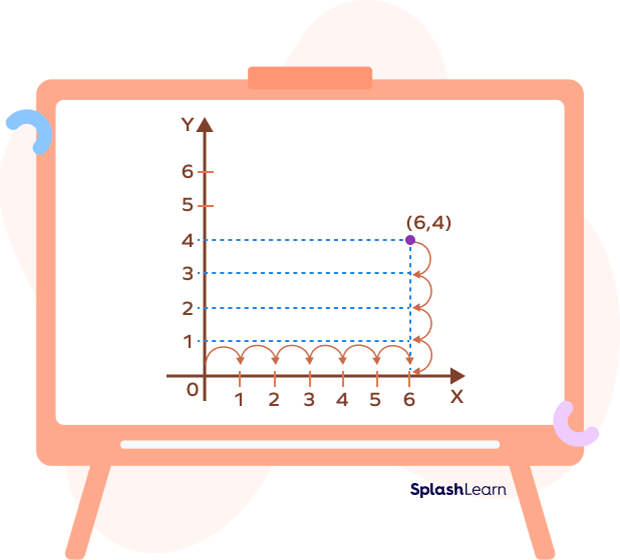
Example: Let’s represent a point (6, 4) on a coordinate plane using the two axes. The point is 6 units away from the y-axis, and 4 units away from the x-axis.
Different Meanings of Axis
Let’s understand how we use the word “axis” in different contexts.
Coordinate Geometry
In a coordinate plane, we can locate any point on the plane using two axes (plural of axis). The coordinates of any point are written as an ordered pair (x, y), where x represents the distance of the point from the y-axis; and y represents the distance of the point from the x-axis.
In the 3D coordinate system, there are three axes: x, y, and z. So, the coordinates of any point are given in the form (x, y, z).
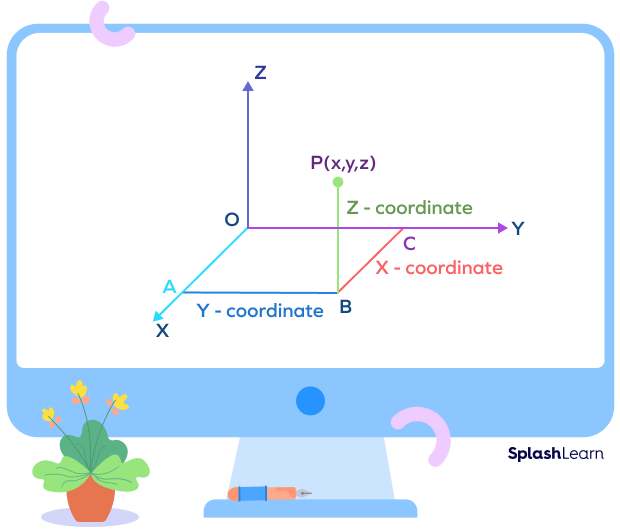
Axis of Symmetry
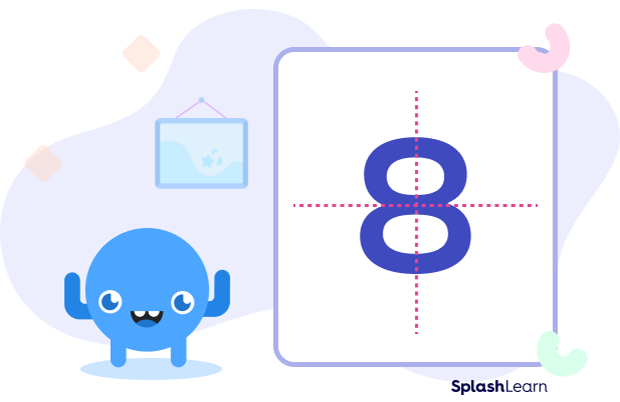
An axis of symmetry is a line that divides a shape such that the resulting shapes on both sides of the figure are mirror images of each other. We can find the axis of symmetry for a mathematical function or even for a physical object.
The following image shows two axes of symmetry or two lines of symmetry for the number 8.
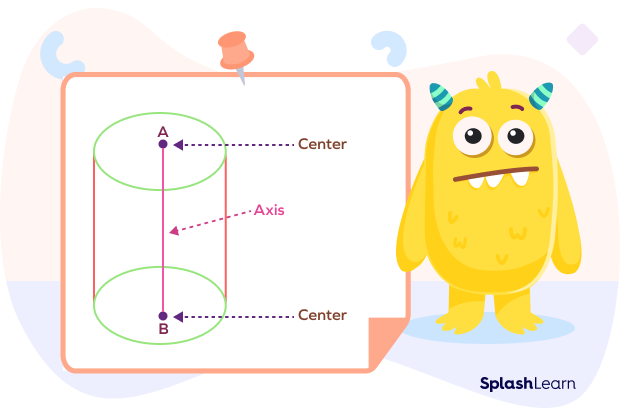
Axis of a Solid
Axis of a solid is considered to be an imaginary line that passes through a solid object. Usually, it passes through the center of the solid object.
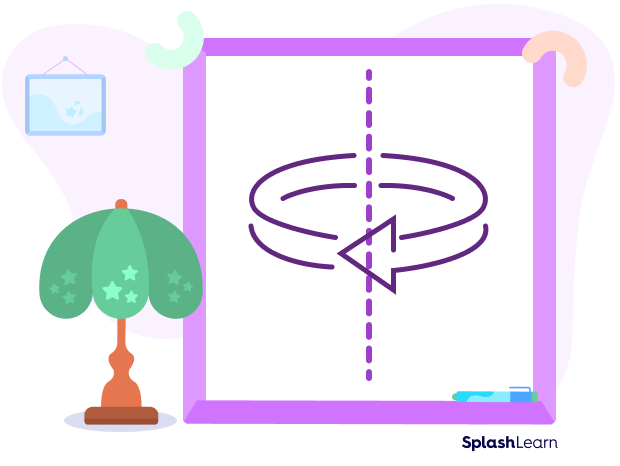
Axis of Rotation
The axis of rotation is a line along which a solid object rotates. If we rotate a disc around a fixed line passing through its center, the line is called “axis of rotation.”
Conclusion
Now you know the axis math definition. The x-axis and y-axis are the horizontal and vertical lines drawn on a Cartesian plane. Using this plane, we can plot any coordinates on a graph to depict the relative position. The intersection of these two axes forms an origin and divides the plane into four different quadrants. Take a look at the fun examples and practice problems shared above to understand how best to deal with mathematical concerns relating to the axis. The detailed problems will help you understand the concept of the Cartesian plane in great depth.
Solved Example on Plural of Axis
1. Show the four quadrants of a Cartesian plane along with the signs of coordinates of any point.
Solution:
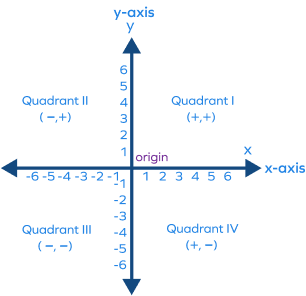
First Quadrant (Top right)
Second Quadrant (Top left)
Third quadrant (Bottom left)
Fourth Quadrant (Bottom right)
As you can see, the following is a Cartesian plane showing the two axes (plural axis) and the four quadrants resulting from the intersection of the two axes.
2. How will you plot the coordinates (2, 3) on the Cartesian Plane?
Solution:
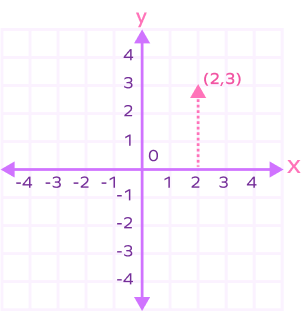
To plot the coordinates (2, 3) on the Cartesian plane, we will need to identify the value of the x-axis and the y-axis, which are 2 and 3, respectively. We will plot the values 2 on the x-axis and 3 on the y-axis. Both values are positive, so the coordinates must lie in the first quadrant.
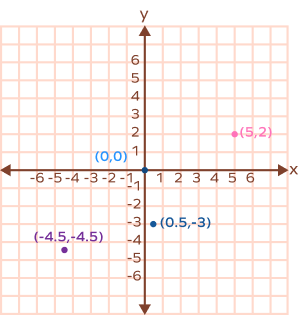
3. Plot the following coordinates on a Cartesian plane.
$(0, 0)$
$(5, 2)$
$(\;-\;4.5, \;-\;4.5)
$(\frac{1}{2}, \;-\;3)$
Solution:
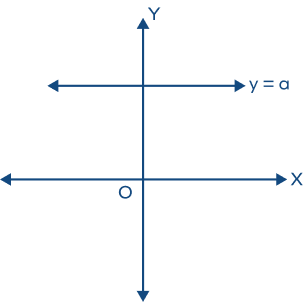
4. If we draw a graph for the equation $\text{y} = \text{a}$, how can we best describe the position of the resulting line?
Solution:
Since we will plot a line for a given value of y, it will be a horizontal line, a line parallel to the x-axis.
5. Draw a Cartesian Plane to show all the four quadrants of the plane. Also, represent any point in each quadrant.
Solution:
Practice Problems on Plural of Axis
Plural of Axis (Axes)
What is the name of the vertical line on a Cartesian Coordinate Plane?
On a Cartesian Coordinate plane, the y-axis is the vertical line, whereas the x-axis is the horizontal line.
The coordinates in the first quadrant for any point can be denoted in which way?
In the first quadrant of the Cartesian Plane, both the x-axis and y-axis are positive as we move to the next quadrant, the sign changes.
Where would the point $(\;-\;2, 3)$ lie on the Cartesian Plane?
In the given case, the coordinates -2 indicate the x-axis, whereas 3 indicates the y-axis. This means that the x-axis is negative while the y-axis is positive, which indicates the coordinates lying in the second quadrant.
On a Cartesian Plane, where do the x-axis and y-axis intersect each other?
A Cartesian plane is defined by the intersection of the x-axis and the y-axis at the coordinates $(0,\; 0)$, where the values are neither positive nor negative.
On which axis would the coordinates $(0,\; 4)$ lie?
The value 0 indicates the coordinates are located on the y-axis itself. Looking at the value 4, we can say it lies on the y-axis and on the positive side since the value is not negative.
Frequently Asked Questions on Plural of Axis
What do you mean by a Cartesian Plane?
In mathematical terms, a Cartesian Plane is a type of coordinate plane with two dimensions. It is formed by the intersection of two lines called axes in math. The said axis in math is the x-axis and y-axis, respectively.
What is abscissa and ordinate?
In the context of the Cartesian plane, the term abscissa is representative of the value of x-coordinates. At the same time, the ordinate represents the value of coordinates on the y-axis.
What are the polar coordinates?
Polar coordinates are represented by $(\text{r},\; \theta)$, where r is the distance of the point from the origin, and $\theta$ is the angle made by the radius vector r with the positive x-axis
Are the x-axis and y-axis on a Cartesian Plane perpendicular to each other?
Yes, the x-axis and y-axis intersect each other at a right angle on a Cartesian Plane, making them perpendicular to each other. Due to this intersection, we get the four quadrants on a Cartesian Plane.
How can we represent the Cartesian Coordinate system in one dimension?
To represent the Cartesian Coordinate system in one dimension, we will need to draw a straight line choosing a point that marks the origin, such that it lies in the center of the straight line.
















