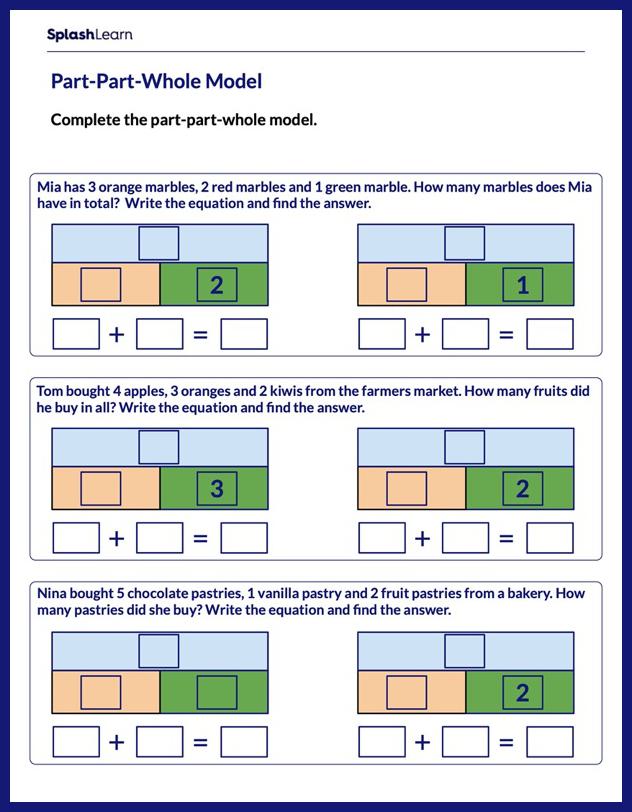
What is a Bar Model in Math?
A bar model is one such tool that helps us visualize the given math problem using different-sized rectangles or bars. The size of the bars are proportional to the numbers that it represents.
Let’s take up some bar model examples to understand them better.
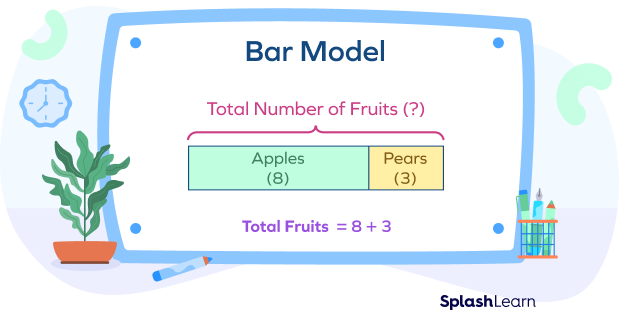
In the given example, the green bar represents 8 apples, and the yellow bar represents 3 pears. And their combination represents the total number of fruits, that is, $8 + 3$.
We can represent other operations like subtraction, multiplication, and division using a bar model, too. We can also show a comparison of numbers using this model.
Recommended Games
Types of Bar Models
The different types of bar models include
- Part-Part-Whole Model
- Equal Parts of a Whole Model
- Comparison Model
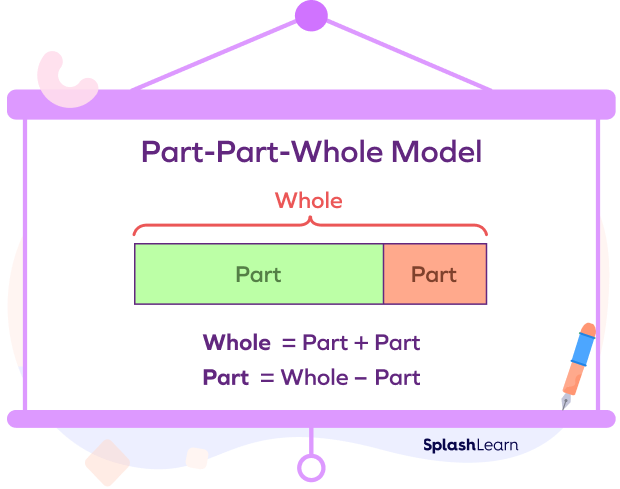
Part-Part-Whole Model
The part-part-whole model consists of two parts that together form a whole. This model can be used to show addition and subtraction.
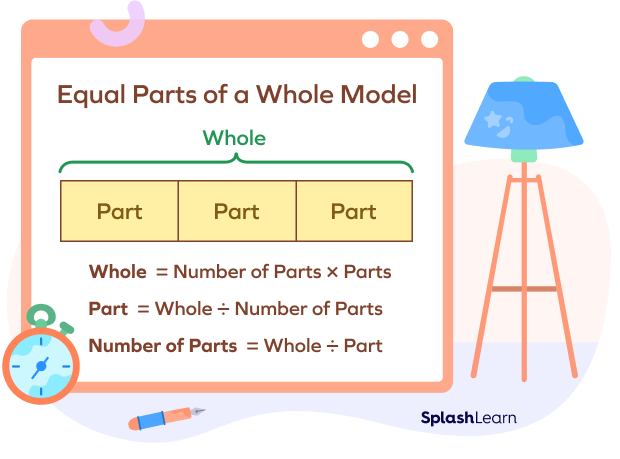
Equal Parts of a Whole Model
The equal parts of a whole model consist of multiple equal parts that together form a whole. This model can be used to show multiplication and division.
Comparison Model
The comparison model consists of two or more bars placed one below the other to compare the quantities.

Recommended Worksheets
Making Bar Models to Solve Word Problems
Bar Model Addition
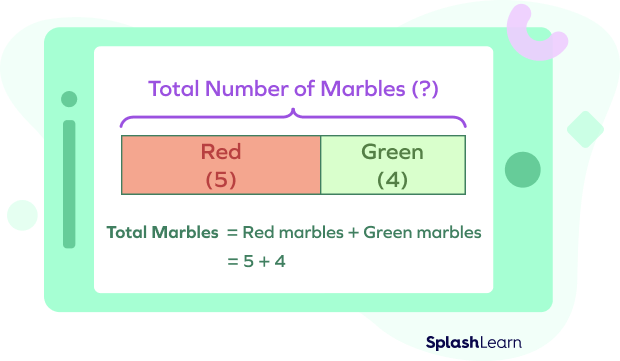
Sam has 5 red marbles and 4 green marbles. Find the total number of marbles with Sam.
In this example, we are given a number of red and green marbles, and we need to find the total number of marbles. This means that the parts are known and the whole is unknown. So, we add the parts to find the whole.
Bar Model Subtraction
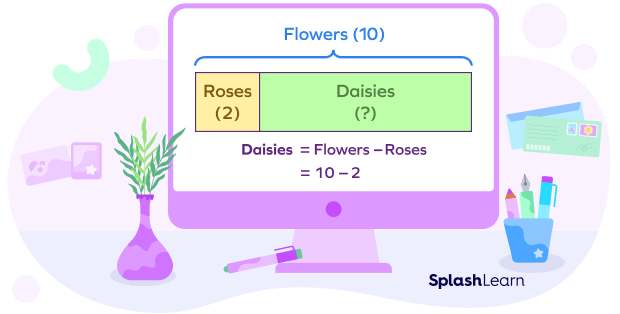
Kate has 10 flowers, out of which 2 are roses and the rest are daisies. How many daisies does Kate have?
In this example, we are given a total number of flowers and the number of roses, and we need to find the number of daisies. This means the whole and one part are known, and the other part is unknown. So, we subtract the given part from the whole to find the other part using the subtraction bar model.
Multiplication Bar model
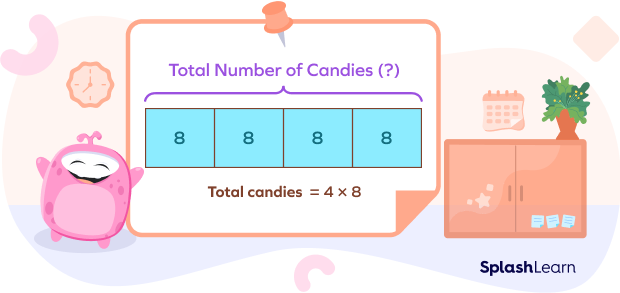
Beth has 4 bags of 8 candies each. How many candies does she have?
In this example, we have candies divided equally among 4 bags. We know the number of bags and the number of candies in each bag. So, we need to find the total number of candies.
According to the model, we know the number of equal parts and the size of each part. So, we multiply them to find the unknown whole.
Division Bar Model
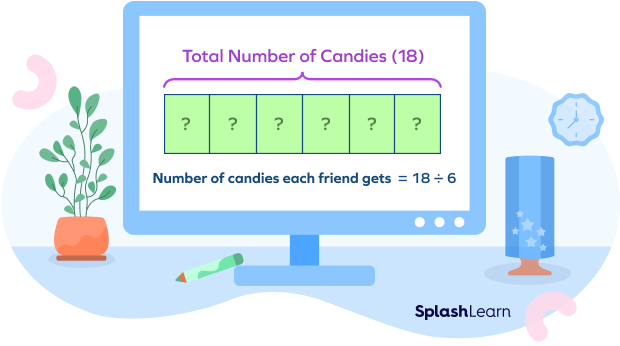
Tim had 18 candies, which he distributed equally among 6 of his friends. How many candies did each friend get?
In this example, we know the total number of candies and the number of friends. That is, the whole and the number of equal parts is known. We need to find the number of candies each friend will get, that is, the size of each part is unknown. We divide the whole by the number of parts to get the answer.
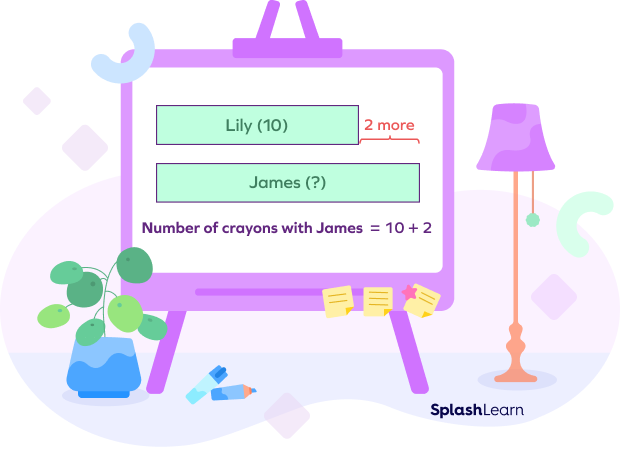
Comparison
Lily has 10 crayons. James has 2 more crayons than Lily. How many crayons does James have?
In this example, the number of crayons with Lily (Quantity A) and how many more crayons James has (difference) is known. We need to find the number of crayons with James (Quantity B).
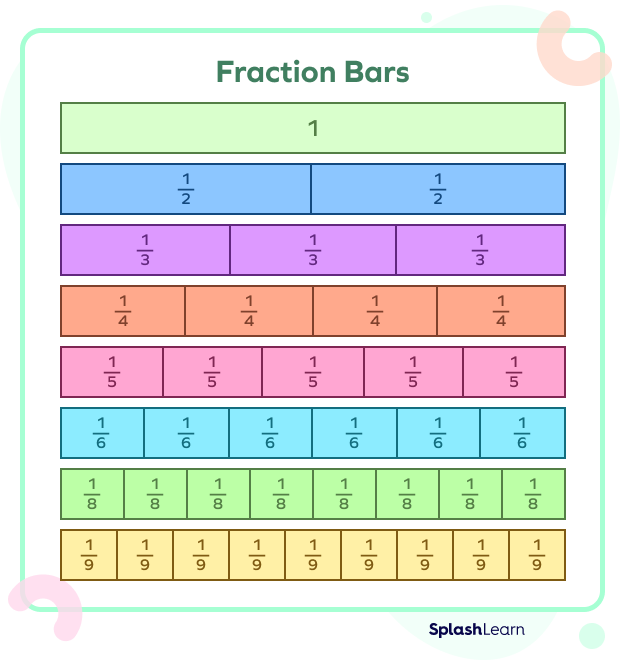
Bar Model Fractions
Bar models can also be used to show fractions, as shown below:
Conclusion
Bar models are a great way to visualize math problems and understand operations like subtraction, addition, multiplication, and division. They can help us compare different amounts and understand parts of a whole.
They can make word problems much easier to solve. Let’s try it!
Solved Examples
Example 1: Write an equation for the given bar model.

Solution:
The model clearly shows that the parts are known, and the whole is unknown.
So the equation that represents this model is:
$8 + 12 =$ ? = Total Number of Candies
Example 2: Write an equation for the given bar model.

Solution:
The model clearly shows that the total and one of the parts are known, while the second part is unknown.
So the equation that represents this model is:
$56 +$ girls $= 85$
or
$85 – 56 =$ ? $=$ girls
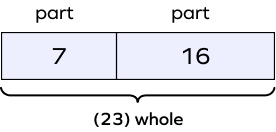
Example 3: What would be the bar model for this equation: $7 + 16 = 23$?
Solution: There are two parts, 7 and 16, that together make 23. So the model would be as follows:
Example 4: Grant has 40 fruit bars. Ken has 15 less fruit bars than Grant. How many fruit bars does Ken have?
Represent this situation using a bar model to find the answer.
Solution:
We know Grant’s number of fruit bars and how many more bars he has than Ken. Clearly, this is a comparison model and can be represented as:

Number of fruit bars with Ken $=$ Number of fruit bars with Grant $– 15$
$= 40 – 15 = 25$ fruit bars
Example 5: Create a word problem for the given model.

Solution:
Nina sells chocolate and vanilla ice cream cones. On a particular day, she sold 13 ice cream cones out of which 10 were vanilla. How many chocolate cones did she sell?
(Please note that there can be multiple answers to this problem.)
Practice Problems
Bar Model in Math - Definition with Examples
Which of the following equations correctly represents the given model?

Because the missing number represents 6 units of the value 12, that is, $6 \times 12 = \underline{}$.
Find the correct value for the missing number.

The bar model shows a large bar of value 24, which is divided into 6 smaller bars. We need to find the value of one small part. This means we need to divide 24 by 6. Here, $24 \div 6 = 4$.
Alex has 84 berries. He wants to eat them over 7 days, eating the same number of berries daily. Use the bar model to find how many berries he should eat daily.
Here, the total number of berries are to be divided equally over 7 days.
So, we need to find $84 \div 7$, which is 12.

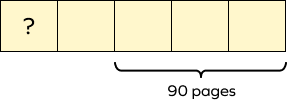
A book consists of 5 chapters. Each chapter has an equal number of pages. Katie has read the first chapter. How many pages has Katie read if the last three chapters are 90 pages altogether? Draw a bar model to find the answer.
The given model represents the situation.
According to the model, if we divide 90 by 3, we will get to know the number of pages in one chapter.
The number of pages in 1 chapter $= 90 \div 3 = 30$.
Since each chapter has an equal number of pages, Katie has read 30 pages.
Frequently Asked Questions
Why do bar models have different-sized boxes?
Bar models have different-sized boxes because the boxes represent different values or quantities. The size of each part shows how much it is as a proportion of the whole.
How can we write an addition statement where the whole and one part in the bar model are known?
We can write it like this: $3 +$ ? $= 24$?
How do bar models help solve math problems?
Bar models help solve math problems because they show us a visual representation of the problem and help us understand the missing number. They also help us compare different numbers or quantities and see how they relate to each other.
Can we represent different forms of numbers such as fractions, percentages, and decimals using a bar model?
Yes, we can represent fractions, percentages, and decimals using bar models.