Meaning of Congruent
If two figures can be placed precisely over each other, they are said to be ‘congruent’ figures.
If you place one slice of bread over the other, you will find that both the slices are of equal shape and size.

The term “congruent” means exactly equal shape and size. This shape and size should remain equal, even when we flip, turn, or rotate the shapes.
Examples of Congruent Figures

Two butterflies which have equal shape and size

Two candy ice creams which represent equal shape and size
Two lego bricks which represent equal shape and size
Symbol of Congruence
Congruence is represented by the symbol- ‘≅’
Since congruence in objects implies equal shape and size; the symbol of congruence is made of two symbols, one above the other. There is a symbol of tilde “” which represents similarity in shape and “=” represents equality in size.
Hence, congruence is represented by the symbol as ‘≅’
If two objects A and B are congruent to each other, we will write it as: A ≅ B
Congruent Line Segments
Since congruence implies equal shape and size, the line segments will be congruent if their shape and size is the same.
Observe the above image carefully.
Since both AB and PQ are line segments they are of the same shape. The length of line segment AB is equal to 5 cm and PQ is also equal to 5 cm. Hence, the length of both line segments are equal to each other.
So, if two or more lines are equal in length, they are said to be congruent to each other.
Hence, the line segments AB and PQ are congruent with each other.
Therefore, it will be represented as line segment AB ≅ line segment PQ.
Congruent Angles
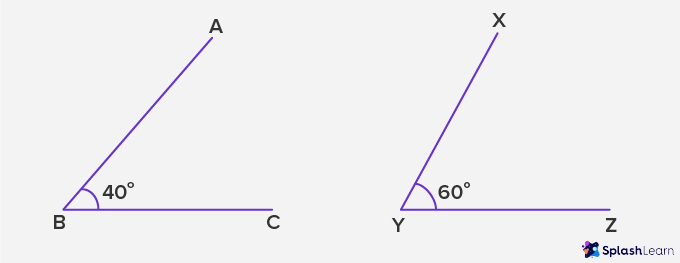
In the above diagram, ∠ ABC = 40°, whereas ∠ PQR = 40°.
If we superimpose or overlap ∠ ABC on ∠ PQR, we will find that both the angles are congruent to each other.
As per the rule, two angles are congruent if the measures of both the angles are equal to each other.
Hence, ∠ ABC ≅ ∠ PQR
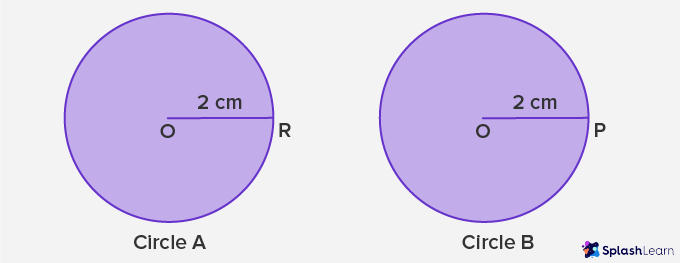
Congruent Circles
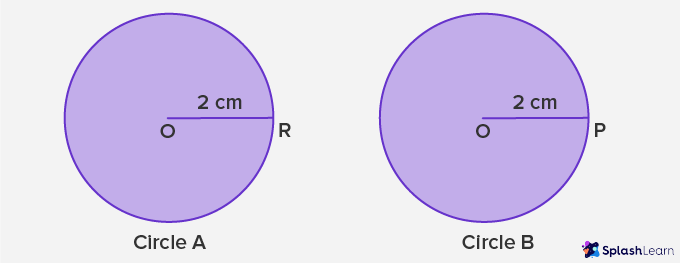
In the above diagram, the radius of Circle A is represented by radius OR, whereas the radius of Circle B is represented by OP.
The shape of both the circles is the same and the size is also the same as the length of radii OR and OP is equal to 2 cm each.
As per the condition of congruency, if the radius of two circles are equal in length, then both the circles are congruent to each other. It also means that both the circles can be easily placed over each other.
To conclude, Circle A is congruent to Circle B, and it can be written as Circle A ≅ Circle B.
Congruent Triangles
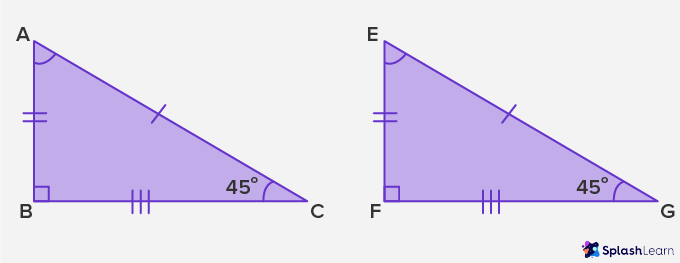
A triangle has 3 sides and 3 angles,so for triangles to be congruent all 3 sides and angles should be congruent.
We observe that:
Side AC = EG, AB = EF and BC = FG,
and ∠ A = ∠ E, ∠ B = ∠ F and ∠ C = ∠ G
Therefore, ABC ≅ EFG.
Whenever two or more triangles are congruent, their corresponding sides and angles are also congruent by the rule of Corresponding Parts of Congruent Triangles (CPCT),
Difference between Congruent Figures and Similar Figures
The significant difference between congruent figures and similar figures is that:
| Congruent Figures | Similar Figures |
|---|---|
| In two congruent figures, both the corresponding angles and the lengths of the corresponding sides are equal to each other. | In two similar figures, the shapes look the same. This is because the corresponding angles are equal. However, the lengths of the corresponding sides are not equal to each other. |
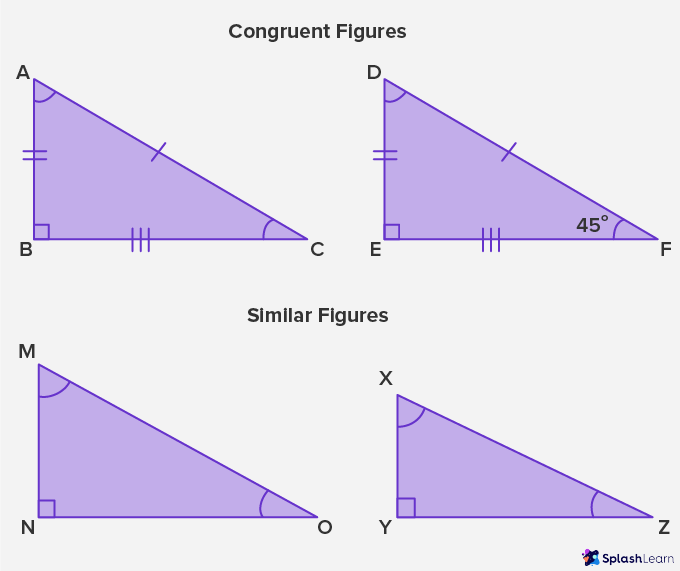
As per the above diagram, Congruent Figures are represented by ABC and DEF, whereas Similar Figures are represented by MNO and XYZ
In regards to Congruent Figures,
Side AC = DF, AB = DE and BC = EF,
∠ A = ∠ D, ∠ B = ∠ E and ∠ C = ∠ F
Therefore, ABC ≅ DEF, as both the corresponding angles and the lengths of the corresponding side are equal to each other.
Whereas, with respect to Similar Figures.
Only the angles are equal to each other, which are ∠ M = ∠ X, ∠ N = ∠ Y and ∠ O = ∠ Z.
The length of the corresponding sides are not equal to each other.
Hence, MNO and XYZ are similar to each other.
However, they are not congruent to each other.
Solved Examples
Example 1: Are the two angles ∠ ABC and ∠ XYZ congruent to each other?
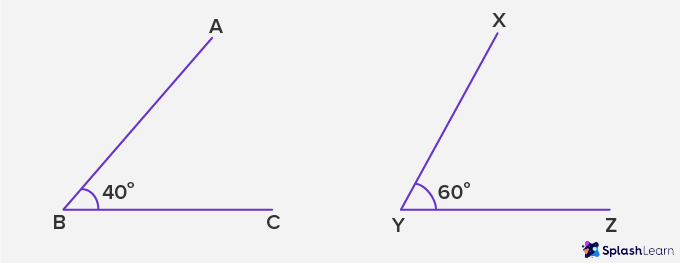
Solution:
The measure of ∠ ABC = 40° and ∠ XYZ = 60°.
As per the rule, two angles are congruent if the measures of both the angles are equal to each other.
Measure of ∠ ABC is not equal to measure of ∠ XYZ.
Therefore, ∠ ABC is not congruent to ∠ XYZ.
Example 2: Two triangles MNO and XYZ are congruent. Mention the corresponding sides and angles that will be equal.
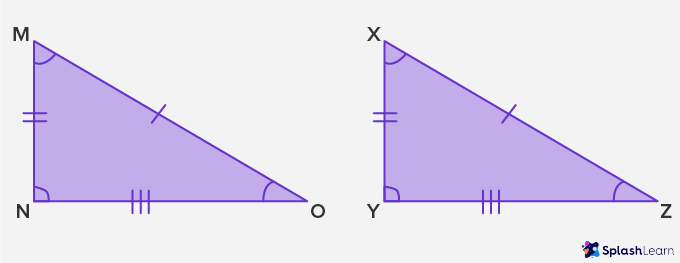
Solution:
Given, ∆MNO ≅ ∆XYZ
As per CPCT, all the three corresponding sides and angles of congruent triangles ∆MNO and ∆XYZ will be equal to each other.
Therefore,
MN = XY
NO = YZ
MO = XZ
Also,
∠ M = ∠ X, ∠ N = ∠ Y and ∠ O = ∠ Z
Example 3: Are the below figures similar or congruent to each other?
In the above diagram, the length of the radius OL is equal to 2 cm, whereas OM is equal to 1 cm.
For two circles to be congruent to each other, the length of the radius of both the circles should be equal to each other.
Therefore, both the circles are similar to each other, but they are not congruent to each other.
Conclusion
We understand that identical shapes and sizes are called congruent in geometry. In congruent figures, the shape and size should remain equal when we flip, turn or even rotate the shapes. And in congruent shape, two figures can be placed over each other.
With SplashLearn, your child can learn about this chapter with solved examples in an exciting way. To strengthen your child’s basics in mathematics, SplashLearn is the best and most trusted platform for every kid. This online educational platform makes learning easy and engaging for your child.
CTA
Are you looking for an online educational platform that is entertaining and educational at the same time? Do you want your child to learn and practice mathematics while having fun? Then, don’t wait too long!
Sign up for SplashLearn and boost your child’s confidence in learning mathematics.
Practice Problems
Congruent1 Find out the false answer in the case of two congruent figures.Congruent figures are equal in size Congruent figures can be overlapped Congruent figures are not equal in shape Congruent figures can be rotated CorrectIncorrect Correct answer is: Congruent figures are not equal in shape The answer is III. Congruent figures are equal in shape too. 2 In the case of two congruent triangles △ABC and △MNO, if angle A is 55°, what is the measure of angle M when it corresponds to angle A?65° 55° 40° None of the above CorrectIncorrect Correct answer is: 55° The answer is II, 55°. In the case of two congruent triangles, corresponding angles are equal. △ABC and △MNO, if angle A is 55°, angle M will also be 55°. 3 If △ABC ≅ △PQR, then which angle will be congruent to∠ R?∠B ∠C ∠A None of the above CorrectIncorrect Correct answer is: ∠C The correct answer is II. If △ABC ≅ △PQR, then angle C will be congruent to corresponding angle R. |
Frequently Asked Questions
When can we say two figures are congruent?
Two figures can be called congruent when they are of the same shape and the same size.
Can congruent shapes be of different sizes?
No, congruent figures cannot have different sizes. Instead, the figures are termed to be congruent if they have the same shape and same size. Figures with same shape and different sizes are said to similar.
Are all congruent figures similar?
Yes, all congruent figures are similar.
Can congruent shapes or figures be mirror images?
Yes, Congruent figures can be considered as mirror images as they have the same shape and same size.
Do congruent circles have the same diameter?
Two circles are known to be congruent if their radius is equal to each other. The length of a diameter is twice the radius. Therefore, congruent circles have the same diameter.
Can stars be congruent?
Two stars can only be considered congruent if both of them have the same shape and size, even when flipped, rotated or overlapped onto each other.
















