Decagon – Definition With Examples

What is a Decagon?

We know that a two-dimensional closed figure having a finite number of sides is known as a polygon. The minimum number of sides required to make a polygon are three. The number of angles in a polygon depends on the number of sides of the polygon. Polygons can be four sided (parallelogram), five sided (pentagon) and so on.

A decagon is simply a ten-sided polygon. 

In the above image, different sided polygons are given. 

One such type of polygon is a decagon having 10 sides. 

Decagon Definition

In geometry, a polygon having ten sides or a ten-sided polygon is called a decagon or ten-gon. It also has ten vertices and ten angles. 

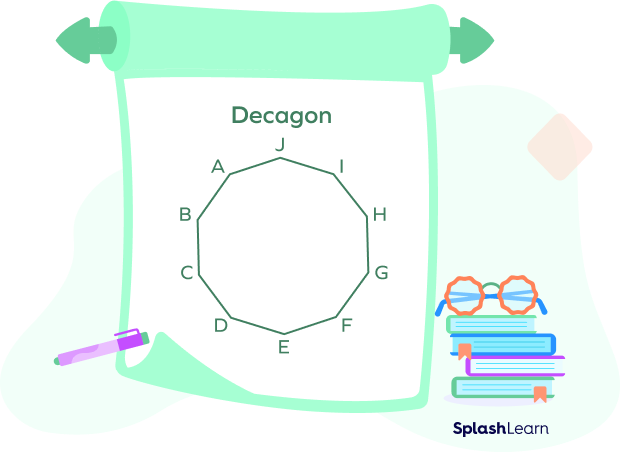
In the above image, there are 10 sides: AB, BC, CD, DE, EF, FG, GH, HI, IJ, and AJ.

There are 10 angles. 

Decagon interior angles: $\angle\text{ABC}$, $\angle\text{BCD}$, $\angle\text{CDE}$, $\angle\text{DEF}$, $\angle\text{EFG}$,$\angle\text{FGH}$, $\angle\text{GHI}$, $\angle\text{HIJ}$, $\angle\text{IJA}$, and $\angle\text{JAB}$

There are 10 vertices: A, B, C, D, E, F, G, H, I, and J. 

Sum of Interior Angles of a Decagon

The sum of interior angles of a polygon $=(n$$-$$2) \times 360^\circ$ where n is the number of sides.

Since the number of sides, i.e., $n=10$ in a decagon

The sum of interior angles of a decagon $=(10$$-$$2)\times180^\circ=8\times180^\circ=1440^\circ$

Thus, the sum of all the interior angles of a decagon $= 1440^\circ$

Types of Decagon

There are three possible ways in which we can classify decagons that are given below:

1. Regular and Irregular Decagons

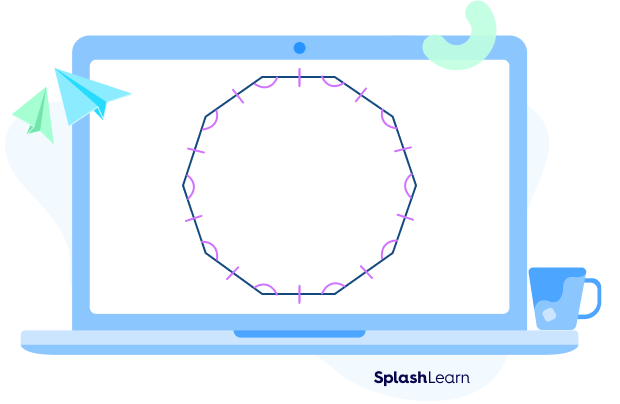
Regular Decagons

Decagons in which all the sides and angles are equal are known as regular decagons. 

The characteristics of a regular decagon are as follows:

a. All the sides are equal in length and all the angles are equal in measure.

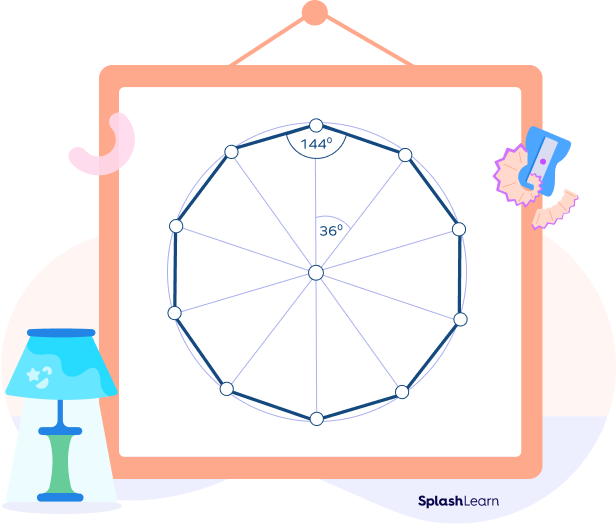
b. Each interior angle of a regular decagon $= \frac{1440^\circ}{10}=144^\circ$

c. Because the sum of exterior angles of a decagon = 360, each exterior angle of a decagon $=\frac{360^\circ}{10}=36^\circ $

d. The central angle is a circle and circle forms $360^\circ $. On drawing 10 diagonals, we get each central angle of a decagon $=\frac{360^\circ}{10}=36^\circ $

e. A regular decagon can be inscribed inside a circle. Also, the circle and the decagon share the same center. 

Irregular Decagons

Decagons in which sides and angles are not equal are known as irregular decagons. There should be at least two sides and angles that are different in measurement. Examples of an irregular decagon are given below:

2. Convex and Concave Decagons

Convex Decagons

Decagons in which all the interior angles are less than $180^\circ $ is known as convex decagons. Or, a convex decagon is a decagon whose diagonals lie inside it. 

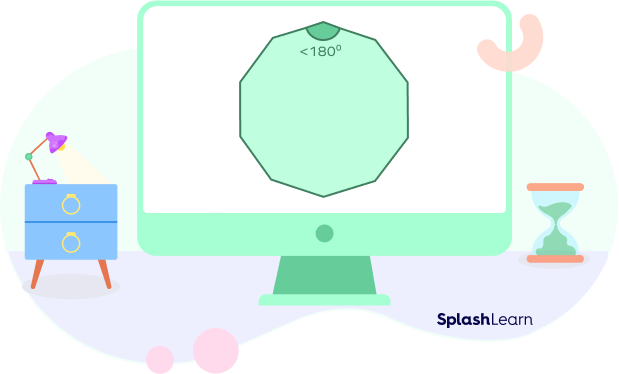
         In the above figure, all the diagonals will lie inside the decagon. 

        Concave Decagons

         Concave decagons are the decagons in which at least one interior angle is greater

         than $180^\circ $. Or, the decagons that have at least one diagonal that lies outside it are known as the concave decagons. 

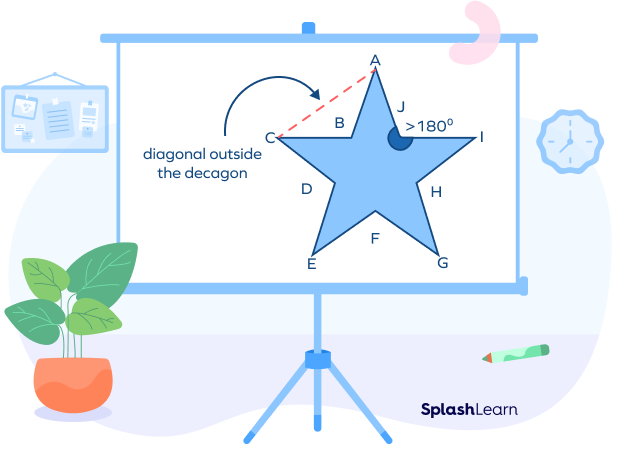
      In the above figure, $\angle$AJI is greater than $180^\circ $ and if we join the vertices A and C, the

       diagonal will lie outside the decagon. 

3. Simple and Complex Decagons

Simple Decagons

Simple decagons are the decagons in which no sides cross each other. Also, the diagonals don’t cross each other. A simple decagon can be regular as well as irregular. 

In the above figure, the decagon is a simple decagon with no sides crossing themselves. 

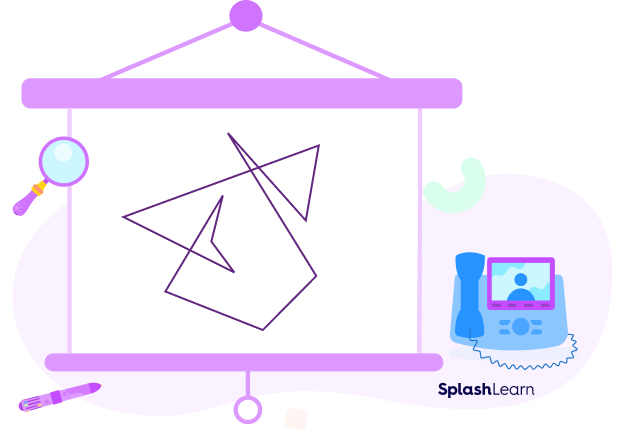
Complex Decagons

Complex decagons are the decagons that are self intersecting and there are additional interior spaces. 

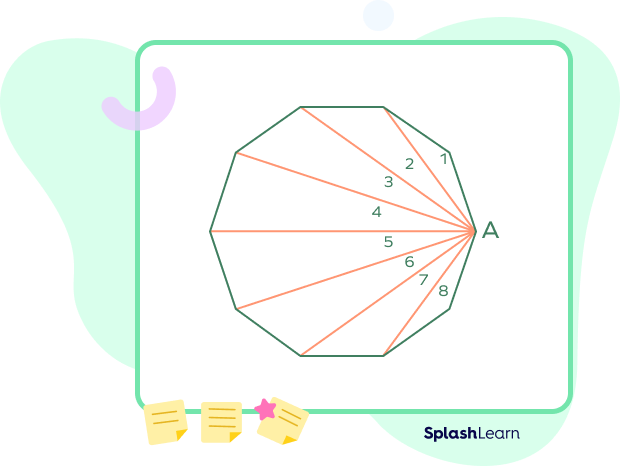
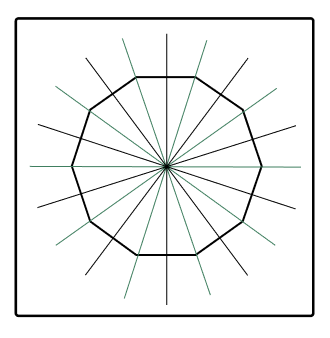
Number of Triangles and Lines of Symmetry in a Decagon

When we join one vertex to the remaining vertices of the decagon, we get 8 triangles. When we join all the vertices independently to each other, then we get $8 \times 10 = 80$ triangles.

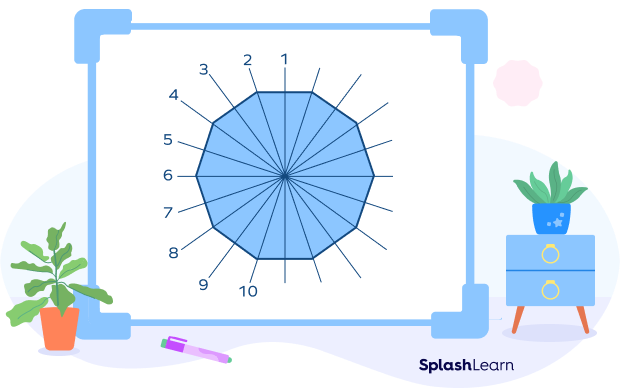
• A regular decagon has 10 lines of symmetry. 

• Irregular decagons may or may not have any line of symmetry. 

Number of Diagonals in a Decagon

The number of diagonals of a polygon $=\frac{n(n-3)}{2}$ where $n$ is the number of sides.

Since the number of sides, i.e., $n=10$ in a decagon

So, the number of diagonals in a decagon $=\frac{10\times7}{2}=35$

Area of a Regular Decagon

Area of a regular decagon is the space occupied between the boundary of the decagon. The formula for area of a decagon is given by: $\frac{5a^2}{2}\times\sqrt{5+2}\sqrt{5}$ where $a =$ length of the side of the decagon.

Decagon Facts

• All sides of a regular decagon are the same length.
• Decagram is a regular star polygon. Its vertex positions are the same as the regular decagon.
• A skew decagon is a skew polygon. It has 10 vertices and edges but not existing on the same plane.

Solved Examples

1. Find the perimeter of a regular decagon if the length of a side is 5 units?

Solution: The number of sides of a decagon $= 10$

Since, the decagon is regular. So, all sides will be equal.

Perimeter $= 5\times10 = 50$ units

2. What is the sum of the number of sides, vertices, and angles in an irregular decagon?

Solution: Number of sides of an irregular decagon $= 10$

Number of vertices of an irregular decagon $= 10$

Number of angles of an irregular decagon $= 10$

Sum $= 10 + 10 + 10 = 30$

3. The two interior angles of a decagon are given 200 and 250. Which type of a decagon is it?

Solution: Since, the two interior angles of the decagon given above are more than 180 so, it is called a concave decagon. 

4. How many lines of symmetry does a regular decagon have? 

Solution: A regular decagon has 10 lines of symmetry. 

Practice Problems

Frequently Asked Questions