- What Are Parallel and Perpendicular Lines?
- Properties of Parallel and Perpendicular Lines
- Difference between Parallel and Perpendicular Lines
- Solved Examples on Parallel and Perpendicular Lines
- Practice Problems on Parallel and Perpendicular Lines
- Frequently Asked Questions on Parallel and Perpendicular Lines
What Are Parallel and Perpendicular Lines?
Parallel and perpendicular lines are two important concepts in geometry. Parallel lines are the lines that never intersect each other. Thus, two parallel lines always maintain a constant distance between them. Perpendicular lines are the two lines that intersect each other at a right angle.
We come across examples of parallel lines and perpendicular lines in daily life. Observe the white lines or stripes in a marked crosswalk. They represent parallel lines. When an analog clock reads 03:00, the minute hand and the hour hand of the clock represent perpendicular lines since they make a right angle (90° angle).
Recommended Games
Definition of Parallel and Perpendicular Lines
Parallel and perpendicular lines play a vital role in geometry. Both of them have distinct properties and applications.
Definition of Parallel Lines
Two lines are said to be parallel if they lie in the same plane and the distance between them is the same. Parallel lines never meet each other. We use the symbol || for parallel lines.
If the lines AB and CD are parallel, we represent them as $AB\; || \;CD$.
Definition of Perpendicular Lines
Two lines are said to be perpendicular if they are intersecting and always meet at an angle of 90°. We use the symbol $\bot$ to represent the perpendicular lines.
If the lines PQ and RS are perpendicular, we write $PQ\; \bot \;RS$.
Let’s take a look at the visual examples of perpendicular lines and parallel lines!
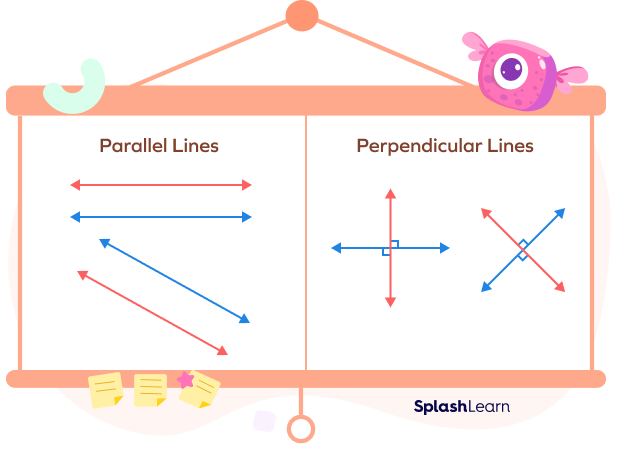
Properties of Parallel and Perpendicular Lines
Let’s discuss a few important properties of parallel and perpendicular lines.
Properties of Parallel Lines
- Parallel lines are always at an equal or same distance from each other.
- Parallel lines never meet even after they are extended infinitely.
- They have the same slope.
Properties of Perpendicular Lines
- Perpendicular lines always intersect at an angle of $90^{\circ}$.
- All perpendicular lines are intersecting lines, but all intersecting lines are not perpendicular because they need to intersect at right angles.
- The product of slopes of two perpendicular lines is $-1$.
Difference between Parallel and Perpendicular Lines
| Parallel Lines | Perpendicular Lines |
|---|---|
| Parallel lines never intersect each other. They are non-intersecting lines. | Perpendicular lines are two intersecting lines. They intersect each other at right angles. |
| We denote parallel lines by the symbol $||$. $AB\; || \;CD$ | We denote perpendicular lines by the symbol $\bot$. $AB \bot CD$ |
| The slopes of parallel lines are equal. | The product of slopes of two perpendicular lines is $-1$. |
| Examples: Tram tracks, Vertical lines in the letter H | Examples: Horizontal line and vertical line in the letter T, Hands of a clock when the analog clock reads 09:00 |
Equations of Parallel and Perpendicular Lines
We represent a straight line through an equation $y = mx + c$ where “m” represents the slope of the line and c is the y-intercept. Two parallel lines never intersect each other and have the same steepness, so their slopes are always equal.
Consider two lines $y = 2x\; – \;1$ and $y = 2x + 3$. We can see that both the equations have the same slope, 2. In mathematical terms, we can express it as $m_1 = m_2 = 2$, where $m_1$ and $m_2$ are the slopes of the lines.
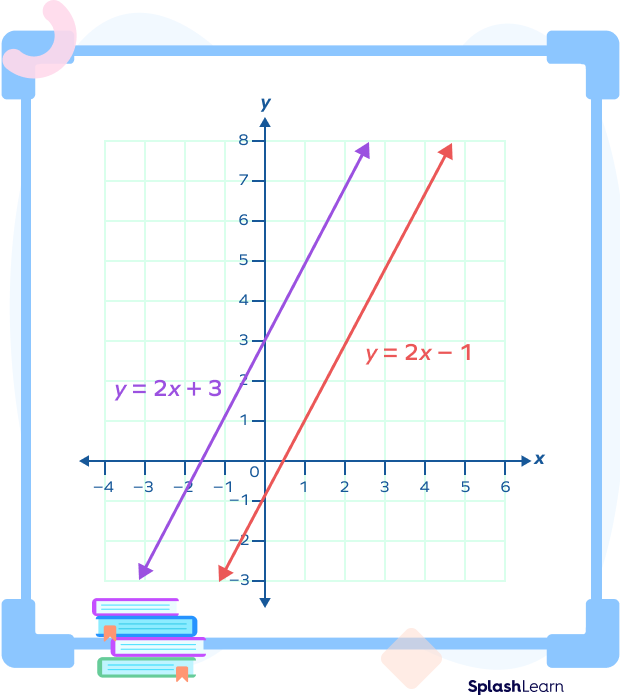
The slopes of perpendicular lines are not the same. The slope of one line is the negative reciprocal of the other line. In other words, their product is $-1$. We can mathematically express it as $m_1 \times m_2 = \;-1$, where $m_1$ and $m_2$ are the slopes of two perpendicular lines.
Suppose we have a two lines $y = 2x +3$ and $y = \;-\frac{1}{2}x \;-\; 1$.
Here, $m_1 = 2$ and $m_2 = \;-\;\frac{1}{2}$.
So, $m_1 \times m_2 = \;-1$.
Let’s plot these perpendicular lines on a graph.
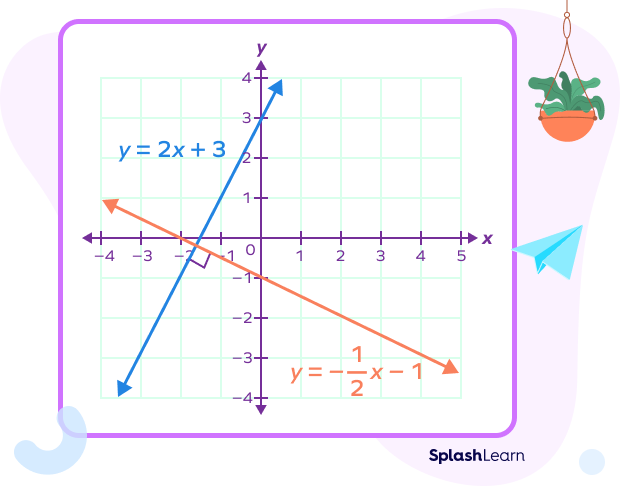
In summary:
- If the slopes of two lines are the same, they are parallel lines.
- if the slopes of two given lines are negative reciprocals of each other, they are perpendicular lines.
Writing Equations of Parallel Lines
Suppose we have a line whose equation is $y = 4x \;-\;3$ and the point on the other line parallel to it is $(2,\;12)$. Here, slopes $m_1 = m_2 = 4$ as the lines are parallel.
We know that equation of line with slope m is $y = m_2 x + c$.
Substituting the values of $(x,\;y)$ and m, we get:
$12 = 8 + c$
$c = 12 \;-\; 8 = 4$
So, the equation of line parallel to $y = 4x \;-\; 3$ is $y = 4x +4$.
Writing Equations of Perpendicular Lines
Suppose we have a line whose equation is $y = 3x + 2$ and the point on the other line parallel to it is (0,1). Here, slopes $m_1 \times m_2 = \;-\;1$ as the lines are perpendicular.
$m_2 = \frac{-1}{m_1} = \frac{-1}{3}$
We know that equation of line with slope m is $y = m_2 x + c$.
Substituting the values of $(x,\;y)$ and $m_2$, we get:
$1 = \frac{-1}{3} \times 0 + c$
$c = 1$
So, the equation of line perpendicular to $y = 3x +2$ is $y = \frac{-1}{3} x + 1$.
Solved Examples on Parallel and Perpendicular Lines
1. Which triangle has perpendicular lines in it?
Solution: Right-angled triangle has perpendicular lines in it.

2. If the slope of one of the two parallel lines is 5, then what will be the slope of the other parallel line?
Solution: $m_1 = 5$
We know that the slopes of two parallel lines are equal, i.e., $m_1 = m_2$.
So, $m_2 = 5$.
3. Find the slopes of the lines $5x + 2y\;-\;6 = 0$ and $-2x + 5y + 3 = 0$. Also, which types of lines are they?
Solution: Converting both the equations in slope intercept form, we get:
$5x + 2y\;-\;6 = 0 \Rightarrow 2y = \;-\;5x + 6y = \frac{-5}{2} x + 3$. So, $m_1 = \frac{-5}{2}$.
$ – 2x + 5y + 3 = 0 \Rightarrow 5y = 2x\;-\;3 \Rightarrow y = \frac{2}{5}x\;-\;\frac{3}{5}$. So, $m_2 = \frac{2}{5}$.
$m_1 \times m_2 = \frac{\;-\;5}{2} \times \frac{2}{5} = \;-\;1$
The lines are perpendicular.
4. State true and false for the following statements. Also, give reason.
a.) The letter V has a set of parallel lines.
b.) The adjacent sides of a square are parallel lines.
c.) Perpendicular lines intersect each other at $90^\circ$.
Solution: V has intersecting lines as they meet each other. They are not perpendicular. Hence, (a) is false.
The angle between the adjacent sides of the square is $90^\circ$ which means adjacent sides are perpendicular. Hence, (b) is false.
(c) is true as the angle between perpendicular lines is $90^\circ$.
5. If two lines are parallel to each other and equation of one line is $y = \;-\;7x + 3$ and the point on the other line is $(2,-5)$, then what will be the equation of the other line?
Solution: Slope of $y = \;-\;7x + 3$ is $m_1 = \;-7$.
Since, the lines are parallel, so $m_1 = m_2 = \;-7$.
We know that equation of line with slope $m$ is $y = m_2\; x +c$.
Substituting the values of $(x,\;y)$ and m, we get:
$-5 = \;-7 \times 2 + c$
$c = \;-5 + 14 = 9$
The equation will be: $y = \;-7x + 9$.
Practice Problems on Parallel and Perpendicular Lines
Parallel and Perpendicular Lines - Definition With Examples
Which of the following is an example of parallel lines?
The opposite sides of a parallelogram are parallel to each other.
Which of the following letters is not an example of perpendicular lines?
L, T and H are the examples of perpendicular lines. N has no perpendicular lines.
If the slope of one of the perpendicular line is $\frac{-3}{4}$, then what will be the slope of the other perpendicular line?
The slopes of a perpendicular line are the negative reciprocal of another perpendicular line.
So, slope of other line $= \frac{4}{3}$.
Which word best describes the lines $3x + 4y \;-\; 6 = 0$ and $12x + 16y +9 = 0$.
$3x + 4y \;-\; 6 = 0 \Rightarrow 4y = \;-\; 3x + 6 \Rightarrow y = \frac{-3}{4} + \frac{6}{4}$. So, $m_1 = \frac{-3}{4}$.
$12x + 16y + 9 = 0 \Rightarrow 16y = \;-\;12x\;-\;9 \Rightarrow y = \frac{-12}{16}\;-\;\frac{9}{16}$. So, $m_2 = \frac{-12}{16} = \frac{-3}{4}$.
$m_1 = m_2$.
Hence, the lines are parallel.
If two lines are perpendicular, then which of the following is true?
If two lines are perpendicular, the slope of them are negative reciprocals of each other.
Frequently Asked Questions on Parallel and Perpendicular Lines
What is the difference between parallel lines and intersecting lines?
Parallel lines are the lines which never intersect each other even if we extend them infinitely whereas intersecting lines meet each other at a point.
Are all intersecting lines perpendicular?
No. Intersecting lines can meet at any angle. But all perpendicular lines are intersecting lines.
What common characteristics do parallel and perpendicular lines have?
The common characteristic is that both have straight lines.
Can a figure have both parallel and perpendicular lines?
Yes. A figure can have both Parallel and Perpendicular Lines. Some examples are: Letter H, Letter E, Square, Rectangle etc.
How many pairs of parallel and perpendicular lines are there in a rectangle?
A rectangle has 2 pairs of parallel lines and 4 pairs of perpendicular lines.


























