What is one of the first things that come to mind when you think of Egypt? The most likely answer to this question would perhaps be the Great Pyramid of Giza.

Looks like a three-dimensional triangle, doesn’t it?
What Is a Pyramid?
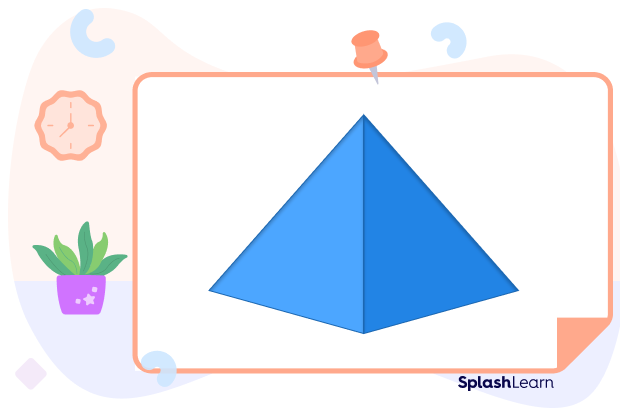
Well, a pyramid is a three-dimensional shape. It has a polygon at the base. It also has sloping sides that meet at a point at the top. The Great Pyramid of Giza that we just spoke about has been constructed using the same concept.
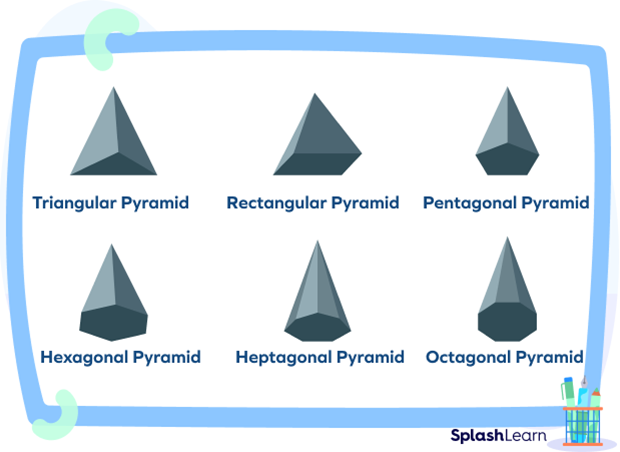
Pyramids come in different types. And what is it that makes them different from one another? It is their base. Different types of pyramids are named after the shape of their bases. For example, a pyramid with a triangle for a base is called a triangular pyramid.
What is a Pentagonal Pyramid?
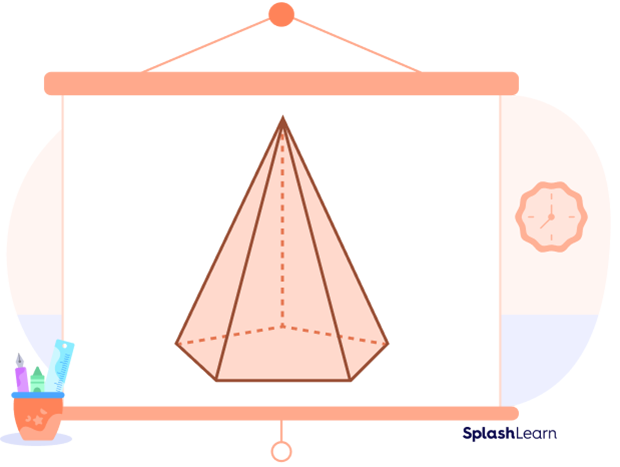
Like all pyramids, a pentagonal pyramid is a three-dimensional shape. It has its base as a pentagon. You already know that a pentagon is a polygon with five sides. In geometry, a pentagonal pyramid is a pyramid with a pentagon as a base upon which five triangles have raised that meet at a point.
Recommended Worksheets
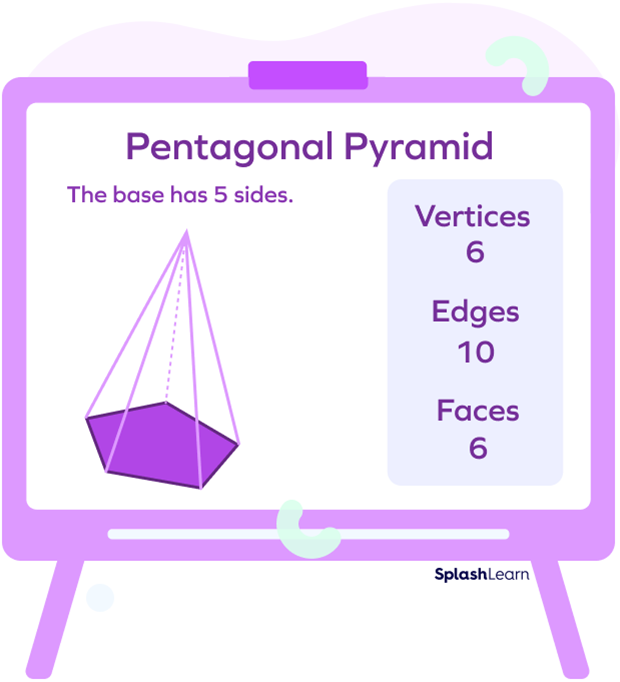
What Are the Properties of a Pentagonal Pyramid?
Now, the general properties of a pyramid apply to a pentagonal pyramid as well. But it doesn’t stop there. Since it has a unique pentagonal base, certain additional properties also come into play. Let us find out some fun things about the properties of a pentagonal pyramid:
- It has 6 faces. It has 5 triangles as lateral sides. It also has a pentagon at the base. (So, $5 +1 = 6$ faces in all)
- It has 6 vertices.
- It also has 10 edges.

How Do We Calculate the Surface Area of a Pentagonal Pyramid?
Let’s figure out how to calculate the surface area of a pentagonal pyramid. The surface area of a pentagonal pyramid is a measure of all its faces. We have already learned that a pentagonal pyramid has 6 faces. Now, we need to get three elements. They are its apothem (a), its base length (b), and slant height (s).
The new term here is the apothem, let us try and understand it. An apothem is a perpendicular (90 degrees) line from the center of a regular polygon to one of the sides.
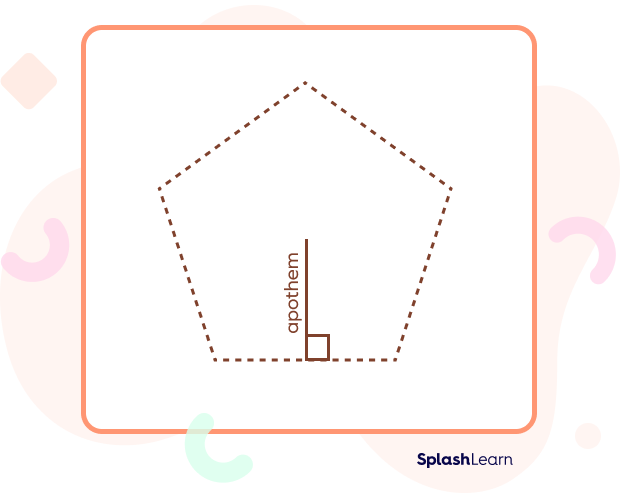
Now that we have understood all three elements, let us learn the formula.
Total surface area of a regular pentagonal pyramid $= 5/2 \times b (a + s)$
How Do We Calculate the Volume of a Pentagonal Pyramid?
Now that we know how the surface area of a pentagonal pyramid is calculated, it makes calculating its volume much simpler. You see, the formula uses pretty much the same elements. Once again we have the apothem (a), base length (b), and height (h). The formula goes like this:
The volume of a regular pentagonal pyramid = (5/6) abh
Solved Examples
Example 1: Which of the following shapes can be the base of a pyramid?
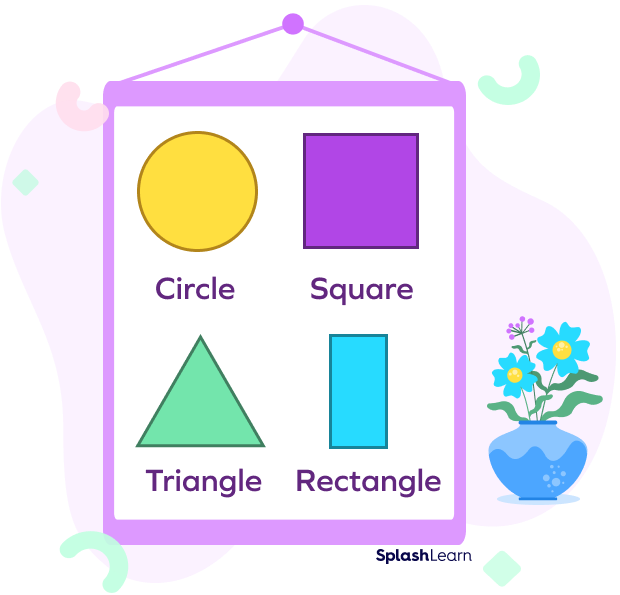
Solution:
The only base of the pyramid is a polygon (no circles or ovals). So, the triangle, rectangle, and square can be the base of a pyramid.
Example 2: A pentagonal pyramid has a base length of 8 inches. Its slant height is 10 inches and its apothem length is 6 inches. Calculate its surface area.
Solution:
In the pentagonal pyramid, the base length is 8 inches, the slant height is 10 inches, and the apothem length is 6 inches.
Therefore, b = 8 inches, s = 10 inches and a = 6 inches
Formula to calculate the surface area of a pentagonal pyramid $= 5/2 \times b(a + s)$
Substituting the values in the formula, we get
$5/2 \times 8 (10 + 6 )$
$= 5/2 \times 8 \times 16$
$= 320$
So, the surface area of this pentagonal pyramid is 320 square inches.
Example 3: Find the volume of a pentagonal pyramid with an apothem of 5 cm, a base length of 9 cm, and a height of 12 cm.
Solution:
In the pentagonal pyramid, the base length is 9 cm, the height is 12 cm, and the apothem length is 5 cm.
Therefore, $b = 9 cm , h = 12 cm$ and $a = 5 cm$
Formula to calculate the volume of a pentagonal pyramid = (5/6) abh
Substituting the values in the formula, we get
$5/6 \times 5 \times 9 \times 12$
So, the volume of this pentagonal pyramid is 450 cm³.
Practice Problems
Pentagonal Pyramid - Definition with Examples
Which of the following is an incorrect statement about a pentagonal pyramid?
A pentagonal pyramid has 10 edges.
How many sides does the base of a pentagonal pyramid have?
The pentagonal pyramid has a pentagon for its base. A pentagon is a polygon made up of five sides.
Identify the pentagonal pyramid from the shapes given below:
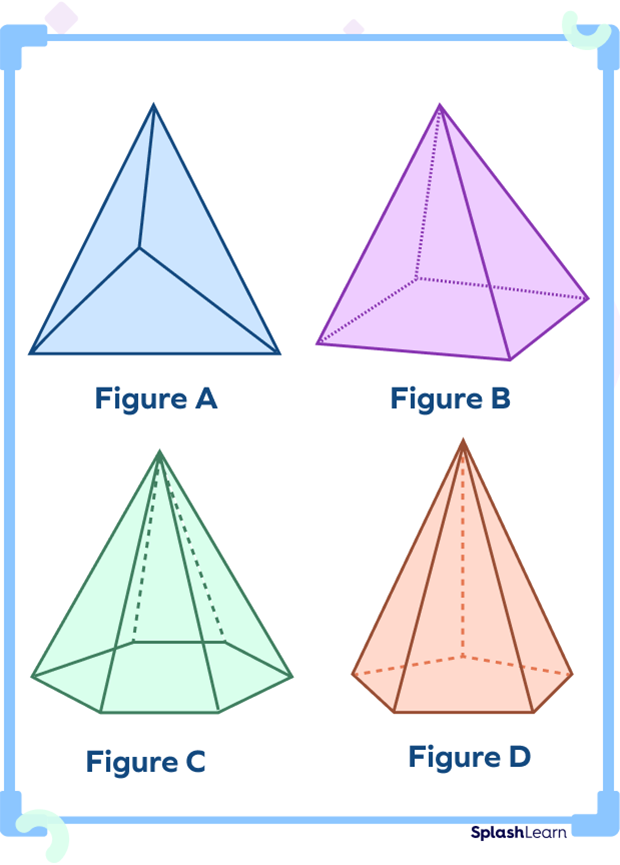
In the image in option D, the pyramid has a pentagon for a base, making it a pentagonal pyramid.
How many faces does a pentagonal pyramid have?
A pentagonal pyramid has 6 faces. It has 5 triangles as lateral sides. It also has a pentagon at the base. (So, $5 +1 = 6$ faces in all)
Frequently Asked Questions
What is the shape of the base of a pentagonal pyramid?
As the name suggests, the base of a pentagonal pyramid is shaped like a pentagon. A pentagon is a five-sided polygon.
How many triangular faces can be found on a pentagonal pyramid?
A total of five triangular faces can be found on a pentagonal pyramid.
Are the faces of the right pentagonal pyramid always equilateral?
The faces of a right pentagonal pyramid could be isosceles or equilateral triangles.



















