What is Plane Geometry?
Plane geometry deals in flat shapes that you can draw on a piece of paper, such as squares, circles, and triangles. Solid geometry deals in three-dimensional solid shapes that exist around us, such as spheres, cones, and cubes.
Suppose you have to draw Earth on a piece of paper. How would you do that? A simple way would be to draw a circle to represent the planet. The Earth you draw will have a flat shape. But the Earth we live on isn’t a flat object. It has a spherical shape.
The branch of mathematics that deals with the shapes, sizes, dimensions, and angles of objects is known as geometry. It is broadly divided into two types: plane geometry and solid geometry.
Today, we shall explore the definition of plane geometry and more. Let’s dive in right away!
Recommended Games
How to Identify a Plane in Geometry?
In geometry, a plane is a flat surface of two dimensions. It extends endlessly and has no thickness. You can think of a piece of paper or the surface of a wall as a part of a geometric plane.
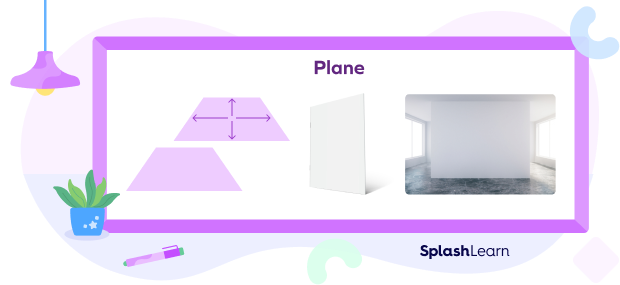
The flat shapes in plane geometry are known as plane figures. We can measure them by their length and height or length and width. But they don’t have any depth.
Some common examples of plane figures are lines, rectangles, circles, and triangles.

Recommended Worksheets
Basic Terminologies in Plane Geometry
When it comes to plane geometry, we need to know about a few terminologies, such as:
- Point
- Line
What Is a Point?
A point denotes an exact location on a plane. It gives us a position, but it has no dimension.
Usually, a dot is used to represent a point. A point often has a name, such as “A”, “B”, “C”, etc.
What Is a Line?
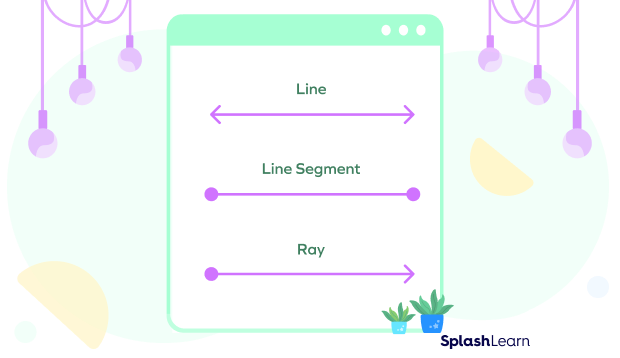
A line is a one-dimensional straight figure. It forms when countless points combine. It has no thickness and extends limitlessly in both directions. We can’t measure its length. A line is represented by two arrows at each end to indicate that it extends endlessly in both directions.
You might have come across the terms, “line segment” and “ray”. They are both parts of a line.
Line Segment: A line segment has two defined endpoints. We can measure its length. An example of a line segment is the edge of a paper sheet. A line segment is represented by a line with no arrows at either end.
Ray: A ray has a defined starting point, but it has no endpoint and can extend endlessly in one direction. We can’t measure its length. A ray is represented by a line with a single arrow at one end to indicate that it extends endlessly in one direction. An example of a ray is a sun ray.
Fun Fact: The Greek mathematician Euclid defined line as a “breadthless length”.
Angles in Plane Geometry
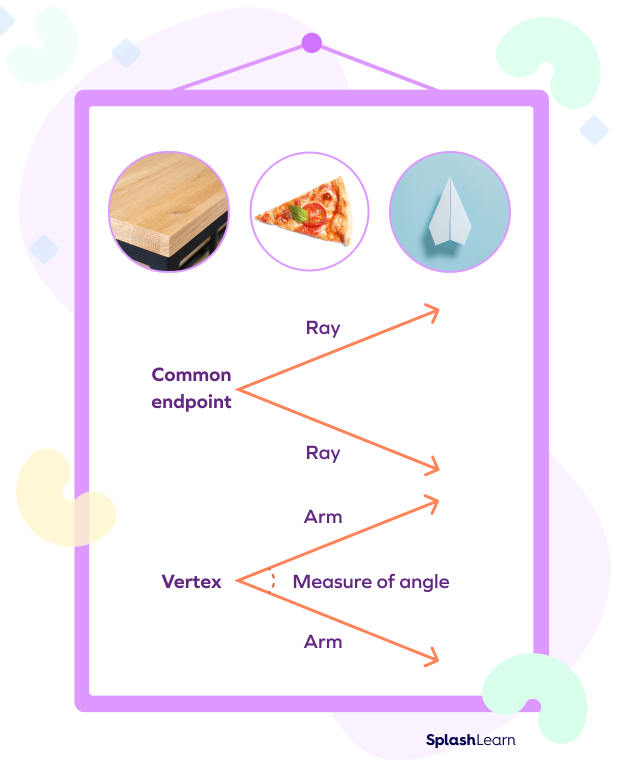
What is common between the edge of a table, an arrowhead, and a slice of pizza? They are all examples of angles we see around us.
An angle forms when two rays meet at an endpoint. The rays are the sides of an angle, while the common endpoint is the vertex.
Angles are measured in degrees (°).
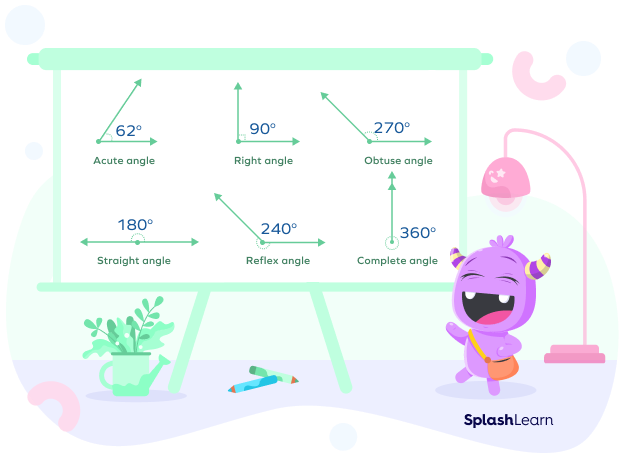
Types of Angles
Acute Angle: An acute angle (or sharp angle) measures between 0° and 90°.
Right Angle: A right angle measures 90°.
Obtuse Angle: An obtuse angle measures between 90° to 180°.
Straight Angle: A straight angle measures 180°.
Reflex Angle: A reflex angle measures between 180° to 360°.
Complete Angle: A complete angle measures 360°.
Plane Geometry Examples
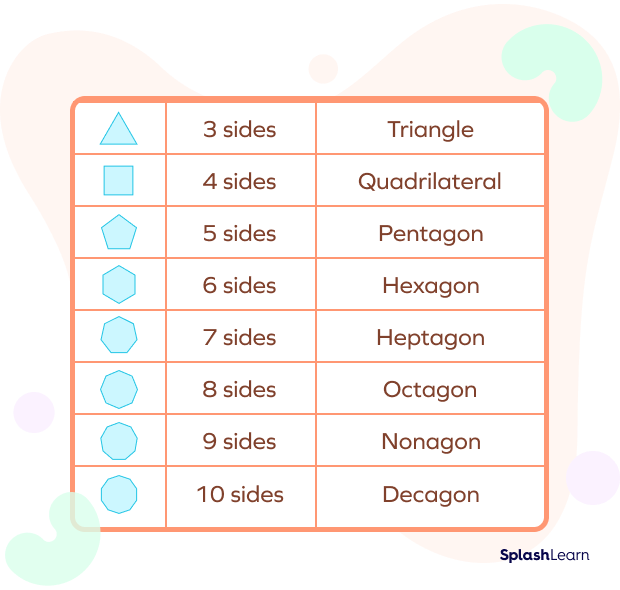
Polygon
A polygon is a closed shape formed by straight line segments. It is a two-dimensional figure with a finite number of sides.
The sides form the edges of a polygon. The meeting point of the two sides is known as a vertex.
A polygon is named depending on its number of sides. It is usually denoted by n-gon, where n is the number of sides. Every polygon has 3 or more sides.
A few examples of polygons are triangles, squares, and rectangles.
Circle in Geometry
A circle is a closed round figure without any edges or corners. It is a two-dimensional curved shape.
The word circle comes from the Greek word kirkos, which means ring or hoop.
The distances between the center of the circle and every point on the circle are the same. This distance is the radius of the circle.

Fun Fact: Flatland is a fictional story by Edwin Abbott, in which he speculates what it would be like to live in a two-dimensional world (a plane). Think for a while about what changes it will bring to your world if such a thing happens!
Conclusion
Knowledge of plane geometry is essential for measuring lines, angles, and surfaces. It lays the foundation for learning solid geometry.
Solved Examples
Example 1: Is the figure below a line or a line segment?
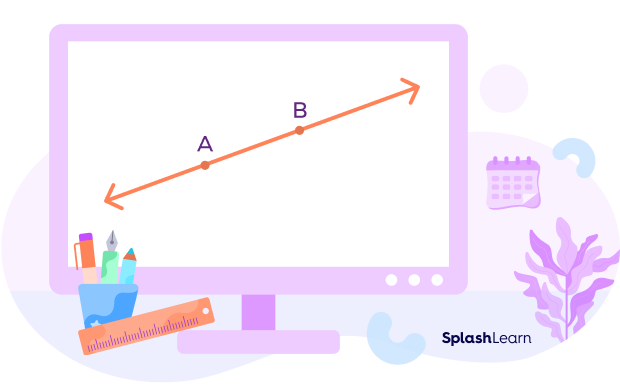
Solution: The given figure is a line. Even though it has two defined points A and B, the two arrows indicate that it extends endlessly in both directions. This shows it is a line.
Example 2: Which of the following figures is not a polygon?
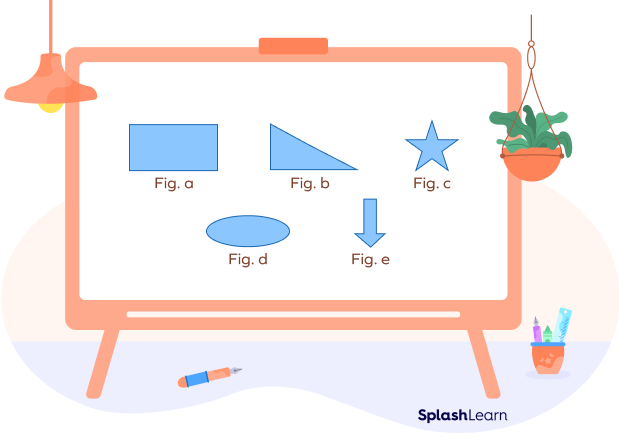
Solution: Fig: d is not a polygon. It is a curved shape, and polygons are formed by straight line segments.
Example 3: Identify the obtuse angles in the following intersection of lines.
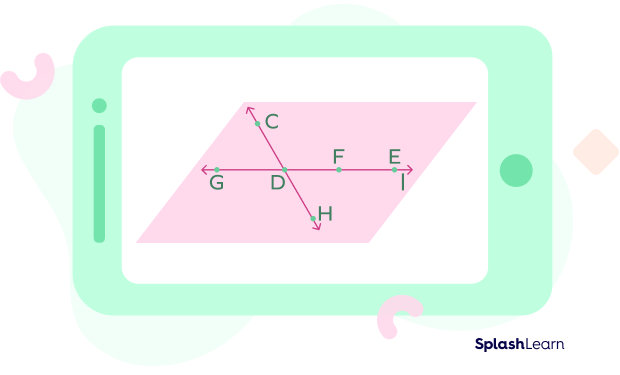
Intersection of LinesSolution: Here, ∠CDE and ∠GDH are the two obtuse angles. They are greater than 90° but less than 180°.
Practice Problems
Plane Geometry - Definition With Examples
Which of the following is an incorrect statement?
In geometry, a plane doesn't have any thickness.
How many dimensions does a point have?
A point has no dimension.
Which of the following is a reflex angle?
Reflex angles measure between 180° and 360°.
Frequently Asked Questions
Are all 2D shapes polygons?
No, all 2D shapes aren’t polygons. For example, a circle is a 2D figure, but it’s not a polygon.
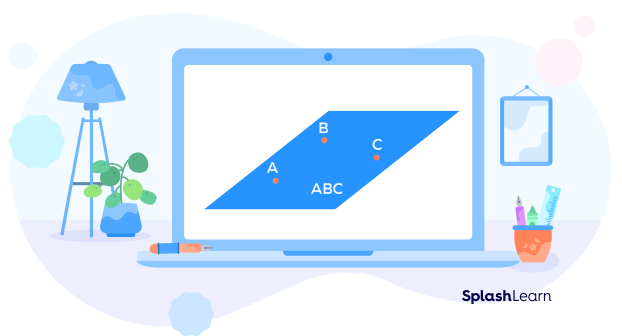
How many points can make up a plane?
Any three points not in a straight line can make up a plane.
What is a regular polygon?
A regular polygon has equal sides and angles.



















