What Is Identity Function?
An identity function is a polynomial function that maps every element to itself. So, the image of any element is the element itself. It is a function in which the output is the same as the input.
Identity function is denoted by “I” and it has the form I(x) = x for all real numbers.
An identity function is also known as an identity map, identity relation or identity transformation. It is known as an identity function because the image of an element in the domain is the same as the output in the range. The identity of the element is maintained.
Recommended Games
Identity Function Definition
Identity function is a real-valued function $f\:R \rightarrow R$ such that $f(x) = x$ for all $x\;\in \;R$.
An identity function maps each real number to itself. The preimage and the image are equal for identity functions.
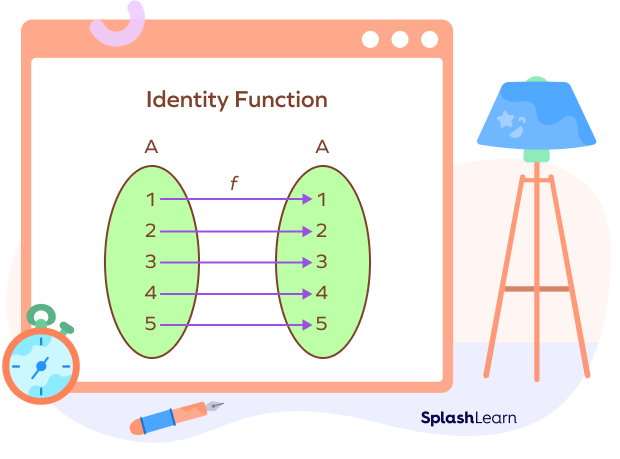
It is noted from the above image that the function f is an identity function as each element of A is mapped onto itself. Hence, the function f is one-one and onto.
Domain and Range of Identity Function
The domain of the identity function is R, the set of real numbers.
The range of the identity function is also R.
The co-domain and the range of an identity function are equal sets.
Hence, the identity function is onto.
Inverse of Identity Function
When we find the inverse of any function, the domain and range of that function gets exchanged. This implies that the identity function is invertible and is its own inverse.
Identity function takes an element and maps it to itself.
Inverse of the identity function (which is itself) again maps the same element to itself.
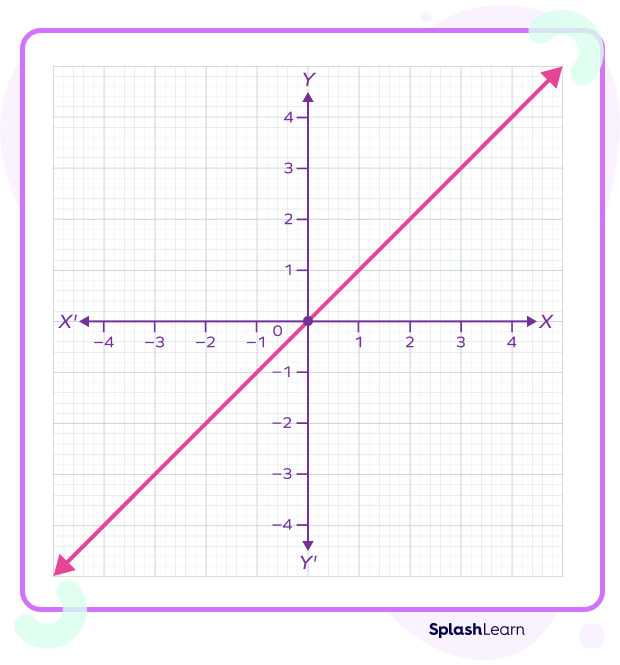
Identity Function Graph
To graph the identity function, we plot the different points as shown below.
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| I(x) | -4 | -4 | -2 | -1 | 0 | 1 | 2 | 3 |
The graph of the identity function is a straight line that passes through the origin.
The straight line makes an angle of 45° with the positive x-axis.
Slope of a straight line = tan θ where θ is the angle between line and positive x-axis.
So, slope of an identity function graph = tan 45° = 1
Properties of Identity Function
- It is a real-valued linear function.
- The graph of an identity function is a straight line that makes an angle of 45° with both x-axis and y-axis.
- Identity function is bijective.
- The inverse of the identity function is the identity function itself.
- Identity function is an odd function since $I(x) /neq I(\;-\;x)$.
Solved Examples on Identity Function
1. If g is an identity function, then find g(0), g(1), g(100), g(6.4).
Solution:
g is an identity function. So, it will return the same value.
g(0) = 0
g(1) = 1
g(100) = 100
g(6.4) = 6.4
2. What is the domain of the identity function?
Solution:
Domain of the identity function is the set of real numbers.
Identity function maps every real number to itself.
3. Define an identity function. What is the graph of identity function?
Solution:
An identity function is defined as a real-valued function f : R → R such that f(x) = x for all x in R.
Its graph is a straight line passing through the origin.

Practice Problems on Identity Function
Identity Function: Definition, Graph, Examples, FAQs
The identity function will map the real number 0 to
The identity function returns the same value.
Thus, I(0) = 0
Which of the following is the domain of an identity function?
The identity function is defined as f: R → R such that f(x) = x.
The identity function has the form
The identity function is defined as f: R → R such that f(x) = x.
Which of the following is a slope of the graph of an identity function?
θ = 45°
Slope (m) = tan 45° = 1
The identity function is
The identity function is bijective. Thus, it is one-one and onto.
Frequently Asked Questions about Identity Function
What is the difference between a constant function and an identity function?
A constant function is a function whose output remains the same irrespective of the input. It is defined as f(x) = c, where x ∈ R. On the other hand, an identity function is a function that returns the same value. It is defined as f(x) = x, where x ∈ R.
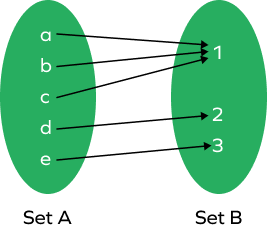
What is a many-to-one function?
According to the many-to-one function, the two or more different elements are mapped to the same image. One example of this function is:
Is identity function even or odd?
Identity function is an odd function.
f(x) = x is an identity function.
f( – x) = – x

















