What Is an Isosceles Trapezoid?
Isosceles trapezoid is a trapezoid in which the top and bottom sides are parallel, while the remaining two non-parallel sides have the same length.
We know that a trapezoid is a quadrilateral with two parallel sides and two non-parallel sides. In an isosceles trapezoid, the non-parallel sides are equal.
Thus, we can say that the parallel sides of an isosceles trapezoid are not equal and equal sides are not parallel. Two base angles in an isosceles trapezoid are equal to one another.
The angles of a trapezoid always add up to 360 degrees, just like any quadrilateral.
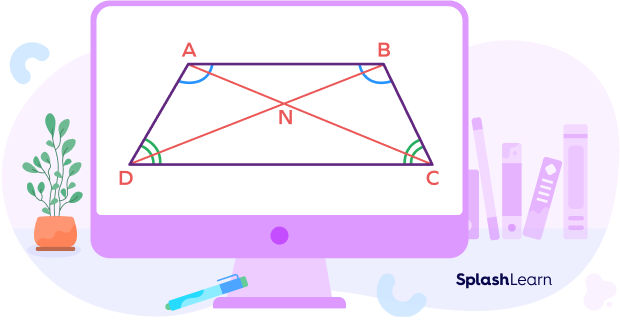
Take a look at the following image to understand the isosceles trapezoid shape.
An isosceles trapezoid can be defined as a trapezoid in which non-parallel sides are of the same length; also the base angles are of the same measure.
Recommended Games
Properties of an Isosceles Trapezoid
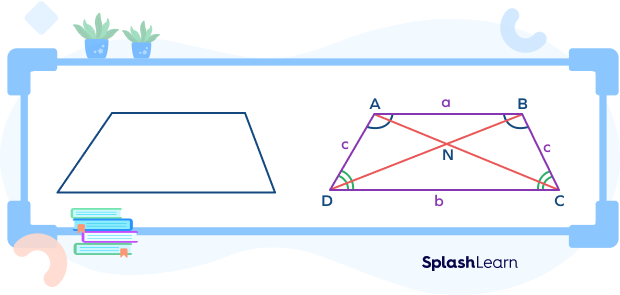
The properties of the isosceles trapezoid are discussed below.
- Only one pair of sides is parallel. $AB | | CD$
- Non-parallel sides (legs) are equal in measure. $AD = BC \Rightarrow c = d$
- The diagonals are equal. $AC = BD$
- The base angles are congruent. $\angle D = \angle C;\; \angle A = \angle B$
- The opposite angles are supplementary. $\angle D + \angle B = 180^\circ;\; \angle C + \angle A = 180^\circ$
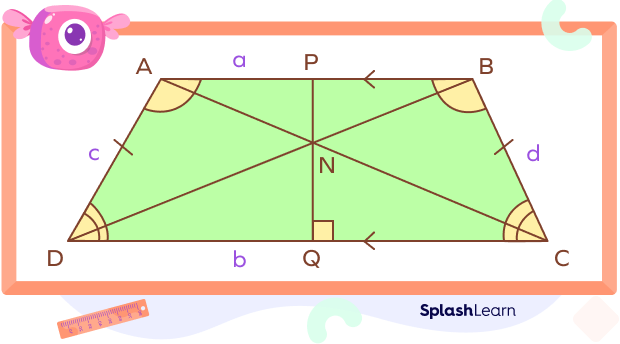
- Line segments joining the midpoints of parallel sides are perpendicular to the base sides.
- A trapezoid can be inscribed in a circle if and only if the trapezoid is isosceles.
- The diagonals divide one another into pairs of segments of equal length.
- It has an axis of symmetry that joins the midpoints of the parallel sides.
Recommended Worksheets
Isosceles Trapezoid: Formulas
Let’s discuss formulas for finding area, and perimeter, median of an isosceles trapezoid.
Median of Isosceles Trapezoid
A line that joins the midpoints of the non-parallel sides creates the midline or the median. The median forms a special theorem that applies only to isosceles trapezoids. The length of the midline is half the sum of the two parallel sides. If we assign the variables a and b to the measurements of the parallel sides, then the length of the median is given by:
$Median = \frac{a + b}{2}$
Perimeter of Isosceles Trapezoid Formula
$P = a + b + 2 c$
Where a, b, and c are the sides of the trapezoid.
Area of the Isosceles Trapezoid Formula
$A = \frac{1}{2} h (a+b)$
where a and b are the lengths of the parallel sides, and h is the distance in perpendicular terms between them.
How to find the Perimeter of an Isosceles Trapezoid
Calculating the perimeter of a shape simply means finding the length around the shape. Let’s understand the steps using an example.
Step 1: Recall the formula. The perimeter of an isosceles trapezoid is given by
$P = a + b + 2c$
The lengths of the sides must simply be added because the perimeter is equal to the sum of the length of the shape’s borders. The legs of this isosceles trapezoid are equal in length, hence you may use 2c in the formula because both legs are identical in length.
Step 2: Replace variables with known values.
Step 3: Write the proper unit as per the question.
Example: Find the perimeter of the given isosceles trapezoid.
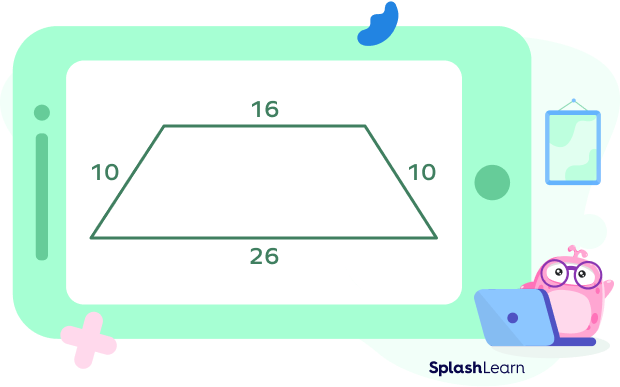
Here, $a = 16$ units, $b = 26$ units, $c = 10$ units
Perimeter $= 16 + 26 + 10 + 10$
$= 16 + 26 + 2(10)$
$= 62$ units
How to Find the Area of an Isosceles Trapezoid
The formula for the area of an isosceles trapezoid is given by
$A = \frac{1}{2} h (a + b)$, where a and b are the base lengths, and h is the height.
Simply substitute the values in the formula. The area is measured in square units. So, apply the appropriate unit to the answer.
Facts about Isosceles Trapezoid
- An isosceles trapezoid’s interior angles add up to 360 degrees.
- The non-parallel sides of an isosceles trapezoid are congruent.
- The median runs parallel to both bases, and its length is equal to the sum of the bases’ lengths.
- “Trapezium” is another name for a trapezoid.
Conclusion
In this article, we learned about isosceles trapezoid, its properties, and formulas associated with it. Let’s solve a few examples to apply what we have learned!
Solved Examples on Isosceles Trapezoid
- Assuming that the isosceles trapezoid has an area of 128 inches2and bases that are 12 inches and 20 inches long, determine its height.
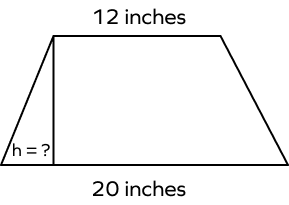
Solution:
Area $= 128\; inches^2$
Bases $= 12$ inches and 20 inches
we know that area of isosceles trapezoid $= A = \frac{1}{2} h(a + b)$
$128 = \frac{1}{2} h(12 + 20)$
Height $= \frac{128}{16} = 8$ inches
2. Calculate the area of an isosceles trapezoid with a height of 4 inches and bases of 3 inches and 5 inches.
Solution: Isosceles trapezoid’s area$ = \frac{1}{2} (sum\; of\; parallel\; sides) \times height$
given, bases $= 3$ inches and 5 inches, height $= 4$ inches
$Area = \left[(3+5) \frac{1}{2} \right]×4$
$Area = 16\; in^2$.
3. Calculate the perimeter.
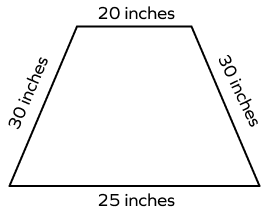
Solution:
An isosceles trapezoid’s perimeter $=$ sum of all sides
Perimeter of an isosceles trapezoid $= 20 + 25 + 30 + 30 = 105$ inches.
4. In a trapezoid, the bases are 2 inches and 4 inches. Find the length of the midline using the median formula.
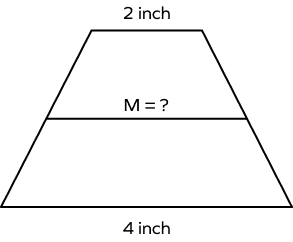
Solution: Median of Isosceles Trapezoid $= \frac{a+b}{2}$.
Where a and b are the parallel sides of a trapezoid.
So, the length of the midline $= \frac{2 + 4}{2} = 3$ inches
5. Determine the perimeter of an isosceles trapezoid with bases of 10 and 15 inches and non-parallel sides of 20 inches each.
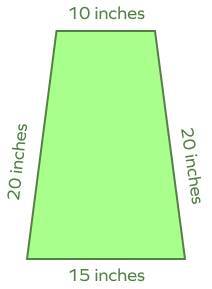
Solution: Perimeter of an isosceles trapezoid $=$ sum of all sides of isosceles trapezoid
Perimeter of an isosceles trapezoid $= 10 + 15 + 20 + 20 = 65$ inches.
Practice Problems on Isosceles Trapezoid
Isosceles Trapezoid: Definition, Formula, Properties, Examples
Which of the following is a property of an isosceles trapezoid?
Isosceles trapezoids have non-parallel sides that are congruent to each other.
Opposite angles of an isosceles trapezoid are ____________.
Opposite angles of an isosceles trapezoid are supplementary.
A trapezoid has legs 8 cm each in length. Its bases are 10 cm and 15 cm respectively. Calculate its perimeter.
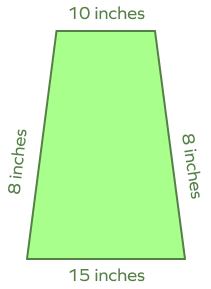
Perimeter of a Trapezoid $=$ Sum of all its sides $= 10 + 8 + 15 + 8 = 33$ inches
In a trapezoid, the bases are 8 inches and 4 inches. Find the length of the midline using the median formula.
Median of a trapezoid $= \frac{1}{2} \times $ Sum of the parallel sides $= \frac{1}{2} \times (8 + 4) = 6$ inches
Calculate the area of an isosceles trapezoid with a height of 6 inches and bases of 8 inches and 4 inches.
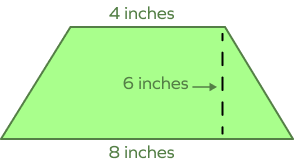
The area of a trapezoid can be calculated if the length of its parallel sides and the distance (height) between them is given.
Frequently Asked Questions on Isosceles Trapezoid
What distinguishes an isosceles trapezoid from a trapezoid?
In an isosceles trapezoid, non-parallel sides are equal, base angles are equal, diagonals are congruent, and opposite angles are supplementary.
Why is it called isosceles trapezoid?
Isosceles means “equal legs.” In an isosceles trapezoid, the non-parallel sides (or legs) are of equal length. Thus, it is called an isosceles trapezoid.
What are the properties of an isosceles trapezoid?
The number of sides in an isosceles trapezoid is four. While the two bases (opposite sides) are parallel to one another, the other two sides are equal in length but not parallel to each other.
What is a right trapezoid?
A right trapezoid is a trapezoid that has two adjacent right angles.
What is the scalene trapezoid?
A trapezoid in which all the four sides are of different lengths is called a scalene trapezoid.






















