What Are Lines of Symmetry in a Rectangle?
A rectangle has two lines of symmetry, one horizontal and one vertical. Each of these lines divide the rectangle into two identical parts. In simple words, you can fold a rectangle into half either horizontally or vertically.
In geometry, a symmetrical figure is a figure that can be folded along a line such that the two parts are identical. The line through which we fold is known as the line of symmetry. A line of symmetry always cuts the shape into two mirror images.
A rectangle is a quadrilateral in which opposite sides are parallel and equal. It has 4 right angles $(90^\circ)$. Since a rectangle is a 2-D shape, it is characterized by two dimensions, length, and width. Length is the longer side of the rectangle and width is the shorter side.
Lines of Symmetry in a Rectangle: Definition
Lines of symmetry in a rectangle are the lines that divide the rectangle into two equal parts.
We know that the opposite sides of a rectangle are equal.
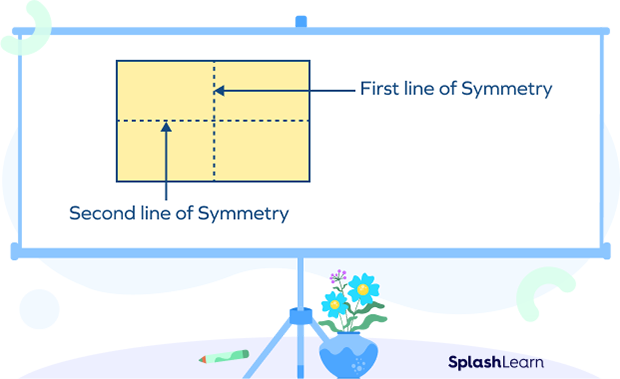
We can try this out by taking a rectangular piece of paper. The simple technique of folding through can help us to find out if a shape has a line of symmetry or not.
If the folded part overlaps the other one, then that folding line is known as the line of symmetry.
In the above figure, each half is placed on the other when the rectangle is folded along the lines of symmetry.
Recommended Games
Why Are Diagonals of a Rectangle Not Lines of Symmetry?
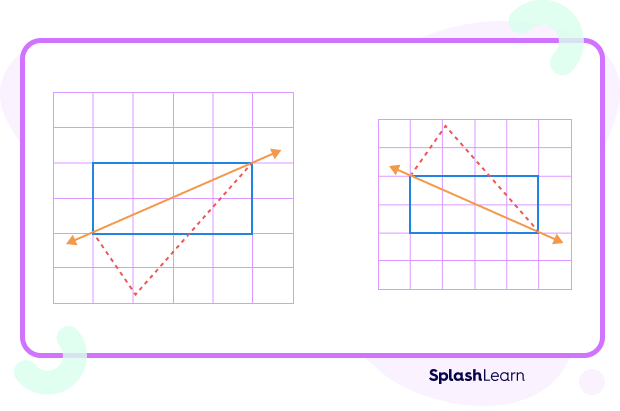
The diagonals of a rectangle are not lines of symmetry as they do not form equal matching shapes on both sides. The two parts of the rectangle formed by a diagonal do not overlap.
This can be seen in the figure given below that why a rectangle does not produce two halves when folded across the diagonal.
Recommended Worksheets
Rotational Symmetry of a Rectangle
If we rotate a figure or a flat shape along its axis and it still appears to be the same as before, we call it rotational symmetry.
In other words, if the shape remains the same as before on partial rotation, then it possesses rotational symmetry.
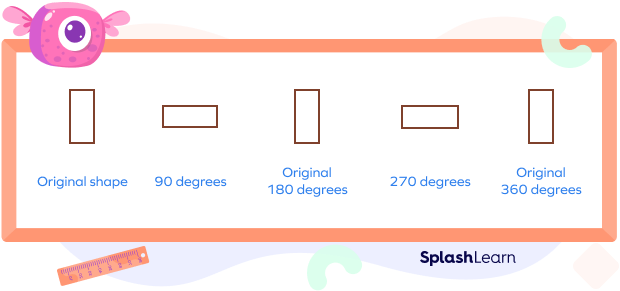
When a rectangle is rotated by $180^\circ$ and $360^\circ$ on its axis, it has rotational symmetry.
In a rectangle, since the length is greater than its breadth, we can say that there is no rotational symmetry at $90^\circ$ and $270^\circ$.
Order of rotational symmetry of rectangle $= 2$.
This means a rectangle comes back to its original position 2 times during rotation of $360^\circ$.
Facts about Lines of Symmetry in a Rectangle
- A square has 4 lines of symmetry.
- A circle has infinitely many lines of symmetry.
Solved Examples on Line of Symmetry in a Rectangle
1. Draw a rectangle and mark the line of symmetry passing through the width.
Solution:
The line of symmetry along the width is the horizontal line of symmetry.
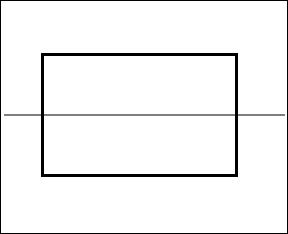
2. Draw a rectangle and mark the line of symmetry through the center along the length.
Solution:
The line of symmetry in a rectangle passing through the length is the vertical line of symmetry.
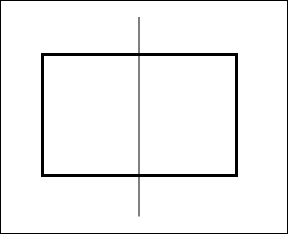
3. Check whether l and m marked in the figure are lines of symmetry in the rectangle given below. Justify your answer.
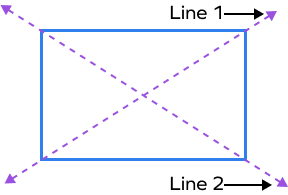
Solution:
Here, l and m are not lines of symmetry because the diagonals of a rectangle do not form lines of symmetry.
4. At which two angles does rotational symmetry not hold for a rectangle?
Solution:
The rotational symmetry does not hold at $90^\circ$ and $270^\circ$ as the length is greater than the breadth.
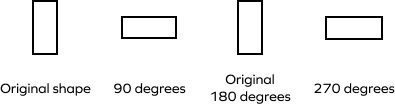
5. Why does the rotational symmetry of the rectangle have order 2?
Solution:
When we rotate the rectangle at $180^\circ$ and $360^\circ$, we get the original rectangle. Hence, the order of rotational symmetry of a rectangle is 2. This means a rectangle comes back to its original position 2 times during rotation of $360^\circ$.
Practice Problems on Line of Symmetry in a Rectangle
Lines of Symmetry in a Rectangle - Definition with Examples
A rectangle has ___ lines of symmetry.
A rectangle has only 2 lines of symmetry – one through the center along length and other along breadth.
The order of rotational symmetry of a rectangle is ___.
We only get the original shape of a rectangle when we rotate it at $180^\circ$ and $360^\circ$.
At what angles a rectangle possesses rotational symmetry?
We only get the original shape of a rectangle when we rotate it at $180^\circ$ and $360^\circ$.
Which of the following are not the lines of symmetry in the figure given below?
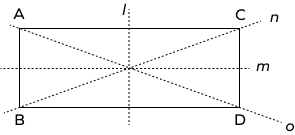
n and o are the diagonals of a rectangle which are not the lines of symmetry.
In how many parts are rectangles divided if we fold it through length and breadth?
The rectangle gets divided into 4 parts if we fold it through length and breadth.
Frequently Asked Questions on Line of Symmetry in a Rectangle
How many lines of symmetry does a square have?
A square has 4 lines of symmetry—one through the center along the length, one along the breadth and two diagonals.
How many lines of symmetry does a scalene triangle have?
A scalene triangle has no lines of symmetry because all sides are of different measure.
How can we find lines of symmetry of any shape?
We can find the line of symmetry of a shape by folding it. If we get two identical halves, then the line will be a line of symmetry.
How many lines of symmetry does a general parallelogram have?
A general parallelogram has no lines of symmetry.
Does a rectangle have a diagonal line of symmetry?
No, a rectangle does not have a diagonal line of symmetry.
How many lines of symmetry does a rectangle have?
A rectangle has 2 lines of symmetry.
Why does a rectangle have 2 lines of symmetry?
In a rectangle, the opposite sides are the equal and all interior angles are right angles. Therefore, it can be folded once along the length and once along the breadth. This way, we get two lines of symmetry.
Can a rectangle have a line of symmetry?
Yes! There are two lines of symmetry in a rectangle, one line through the center along its length and the other is drawn along the width (breadth).



























