Equal Shares: Introduction
To understand the concept of equal shares, let’s first understand what “equal” means.
What is “equal”? “Equal” refers to being the same amount, number, value, shape, and size as something else.
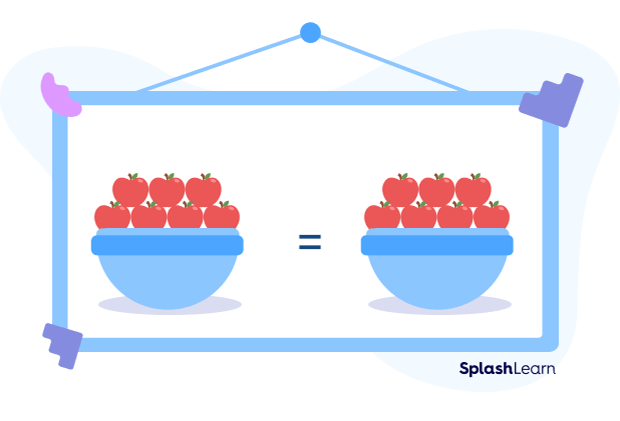
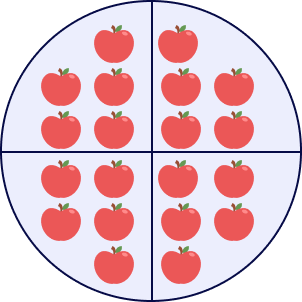
For example, in the figure below, both baskets have the equal number of apples. Each basket has 7 apples.
Recommended Games
What Are Equal Shares in Math?
On dividing the whole or a group of objects into equal parts, we get equal shares.
We need to “divide” an object or a “number” into equal parts in order to distribute it equally. These equal parts have to be the same in measurements like weight, volume, dimensions, numbers, etc. So, equal shares is a simple strategy to teach division.

Recommended Worksheets
Equal Shares Definition
Dividing a number or a collection of objects into smaller and equal groups is called equal sharing.
Equal sharing happens when we know the number being divided and the number of groups but we don’t know the number of items in each group or the size of each group.
Example of equal shares:
8 balloons are to be distributed among 4 kids. How many balloons will each kid get?

Number to be divided $= 8$ and number of groups $= 4$
Size of each group $=$ Number of balloons each kid gets $=$ ?
We can find it by dividing 8 by 2.
$8 \div 4 = 2$. Quotient is 2
So, there will be 4 equal shares and each kid will get 2 balloons.

Equal Shares vs. Equal Groups
In equal grouping, we know the number being divided and the size of each group, but we don’t know how many groups will be formed.
Let’s consider the same example.
Example of equal groups:
8 balloons are distributed among kids such that each kid gets 2 balloons. How many kids are there?
Here, Number to be divided $= 8$ and Size of each group $= 2$
Number of groups $= ? = 8 \div 2 = 4$
Quotient is 4. So, there will be 2 equal groups of 4.
So, in equal sharing, the quotient represents the number of shared objects in each group.
In equal grouping, the quotient represents the number of groups formed.
Equal Shares of a Group of Objects
When shares are equal, each share or group has the same number of objects. The groups which have the same number of objects are called “equal groups.”
Equal shares of objects can be done in many ways, depending on the number of shares or portions we want to create.
For example, 10 kites can be equally grouped as follows:
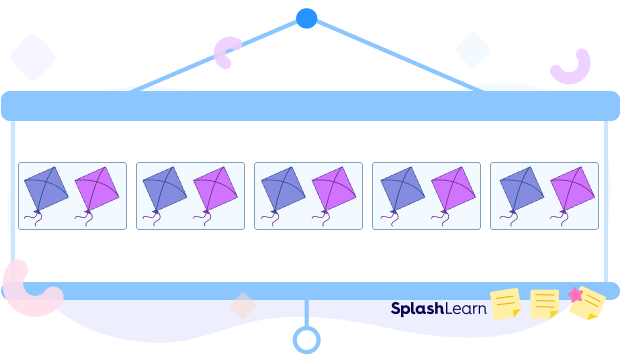
First Way:
There are 10 kites. There are 5 groups.
Each group has 2 kites.
So, 5 groups with 2 kites $= 10$ kites.
You can also write the following expression to represent the situation: $10 \div 5$
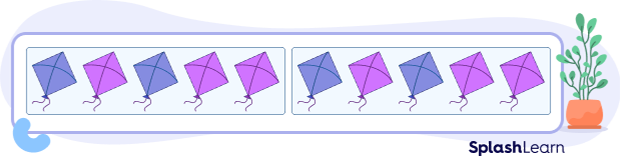
Second Way:
There are 10 kites. There are 2 groups.
Each group has 5 kites.
So, 2 groups with 5 kites $= 10$ kites.
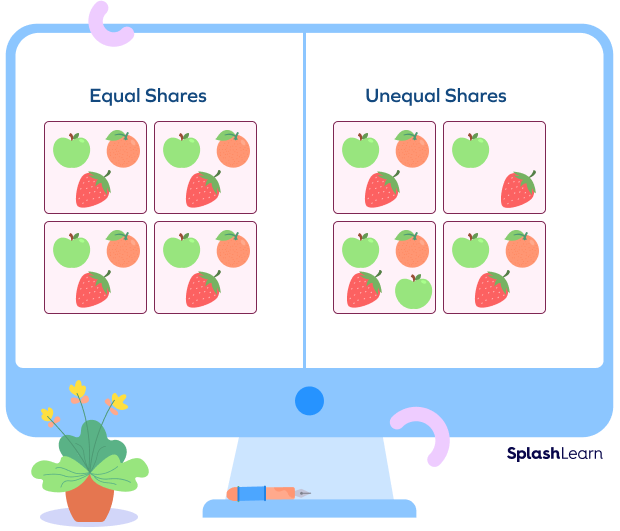
Examples and non-examples of equal shares of a group of objects:
Equal Shares of a Whole
We can also make equal shares of a whole by dividing it into equal parts. A whole could be divided horizontally, vertically, or diagonally to get equal shares.
A simple example of equal shares of an object is cutting a pizza or a cake into equal slices.

Let’s understand this concept more clearly with the help of another example.
Example: Distribute 1 cake equally among 4 friends.
As 1 cake needs to be divided among 4 people, we use 1 in the numerator and 4 in the denominator.
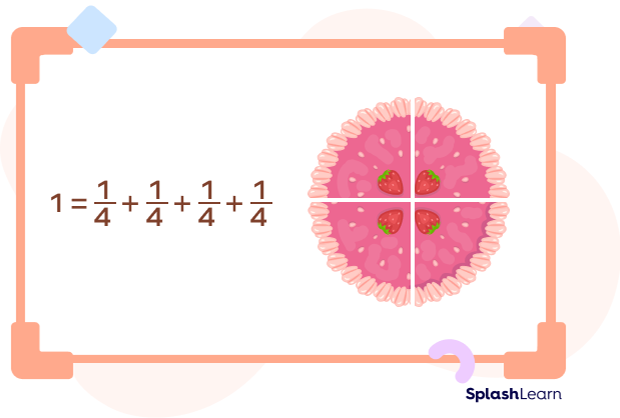
This means that each friend gets a one-fourth share of the cake. It can also be said that each friend receives 1 portion of the 4 equal portions.
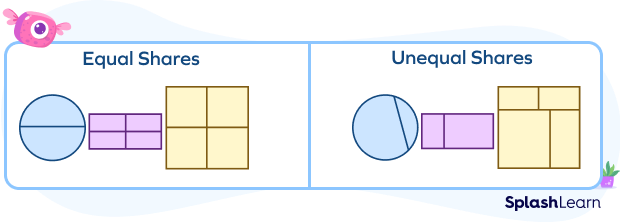
Equal Shares of a Shape
Let’s see some examples and non-examples of equal shares of a shape using images.
Using equal shares, the circle, rectangle and square is divided into equal parts.
Fun Facts!
- Equal shares, when added together, give us the whole.
- Equal shares can be used to divide either a single object or a group of objects equally.
- The result of an equal share can sometimes be a fraction.
Conclusion
Equal shares refer to equal parts of an object or shape. They can exist in different forms, such as circles, squares, rectangles, etc. They can also be grouped in several ways.
Usually, equal shares are introduced in first and second grade and are very helpful in learning division, especially when learning how to divide objects equally.
Solved Examples on Equal Share
1. If we distribute one whole pizza equally among 8 friends, how much pizza will each friend get?
Solution: To divide 1 large pizza among 8 friends, we use 1 in the numerator and 8 in the denominator, as shown in the image below.
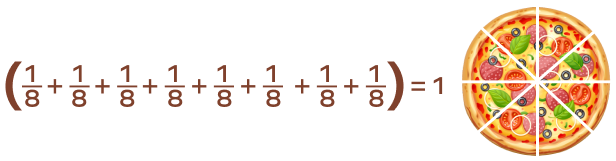
This means that each sibling gets a one-eighth share of the pizza. It can also be said that each sibling receives 1 portion of the 8 equal portions.
2. How does shape A differ from shape B?
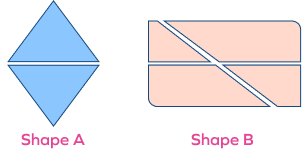
Solution: Observing shape A, we can tell that it is equally divided into 2 parts, while shape B is not equally divided into 4 parts.
3. Shane has 12 muffins. He wants to divide them equally between himself and his two friends, Ben and Ray. How can he share the muffins equally?
Solution:
So, to divide the 12 muffins equally, Shane needs to divide 12 muffins into 3 equal shares.
We know that $\frac{12}{3} = 4$
This means that person will get 4 muffins.

4. June has 20 apples with her. She wants to divide them equally in different boxes. Give any two ways by which she can arrange 20 apples equally in boxes?
Solution:
There are 20 apples in total. June can arrange them in two different ways.
1st way: Two equal shares
$10 + 10 = 20$, as shown in the image below.

So, 20 apples can be arranged in 2 boxes containing 10 apples each.
2nd way: 4 equal shares
Since $5 \times 4 = 20$ and $\frac{20}{4} = 5$
So, 20 apples can be arranged in 4 boxes containing 5 apples each.
5. Which of the following shapes show unequal shares?
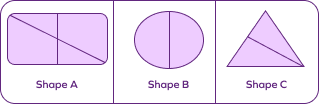
Solution: Observing the shape A, we can tell that it is not equally divided.
Practice Problems on Equal Share
Equal Shares in Math
Find the correct option.
Since, $4 + 4 = 8$. So, 8 can only be arranged into 2 equal shares of 4.
Which of the following shapes is divided into 2 equal shares?
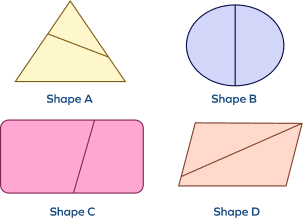
By observing the shape B, it is clear that it is divided into two equal shares.
In how many equal shares can 15 be grouped into?
Since, $3 \times 5 = 15$.
So, 15 can be divided into 3 equal shares of 5 or 5 equal shares of 3.
Find the odd one out.
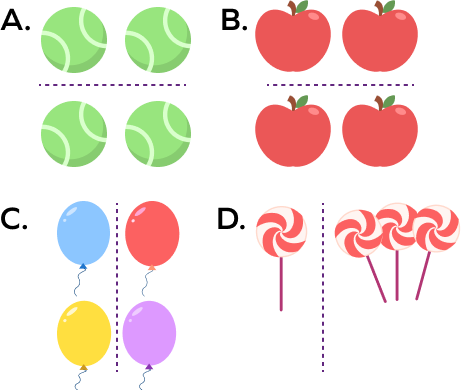
Image D has unequal shares while the others show equal shares. Hence, option D is the odd one out.
30 cupcakes are to be distributed among 5 friends. How many cupcakes will each friend get?
Since, $30 \div 5 = 6$
So, each friend will get 6 cupcakes each.
Frequently Asked Questions on Equal Share
What is another name for equal shares?
Equal shares are also known as uniform distribution.
What is the meaning of whole numbers?
Whole numbers are those that contain natural numbers along with 0.
What is the meaning of a fraction?
A fraction is a part or portion of a whole.
What are 3 equal parts of a shape called?
3 equal parts are known as thirds.
What are 4 equal shares of a shape called?
4 equal shares are known as fourths.




































