Negative Slope: Definition, Graph, Solved Examples, Facts

What Is a Negative Slope?

Negative slope refers to the slope of a line that is trending downwards as we move from left to right. In mathematics, the slope of a line is the change in y-coordinate with respect to the change in x-coordinate.  

So, what does negative slope mean? A negative slope means that two variables are negatively related. When x increases, y decreases. 

A line that makes an obtuse angle (an angle greater than 90 degrees) with the positive x-axis in the counterclockwise direction is known as a line with a negative slope. If the line makes an acute angle with the positive direction of the x-axis, the line has a positive slope. A simple real-life example of negative slope is going down a hill.

Negative Slope: Negative Rise Over Run Ratio

We know that the slope is given by the rise over run ratio.

Slope $= m = \frac{Rise}{Run} = \frac{\Delta y}{\Delta x}$

We can also say that a line has a negative slope when it has a negative rise over run ratio. Rise is the change in y-coordinates, and run is the change in x-coordinates. Let’s take a look at example of the negative slope equation with graphs showing rise over run ratio.

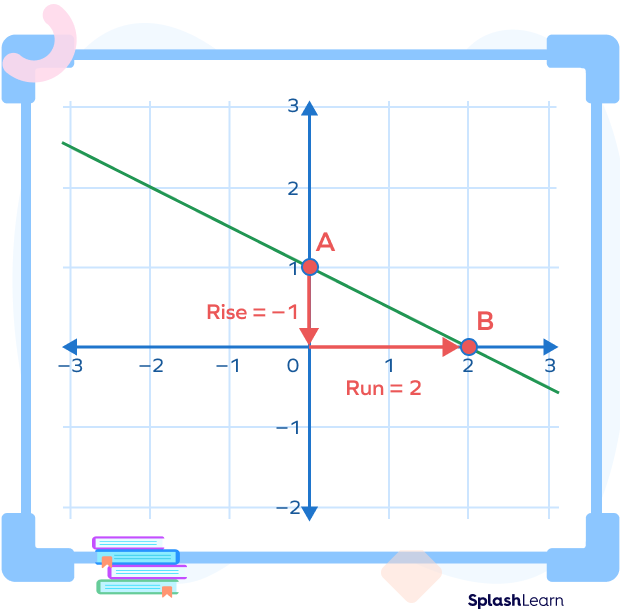
Example 1: Here, the line AB has a slope of $\frac{-1}{2}$.

Equation of line is $y = \frac{-1}{2}x + 1$

Slope $= \frac{Rise}{Run} = \frac{-1}{2}$

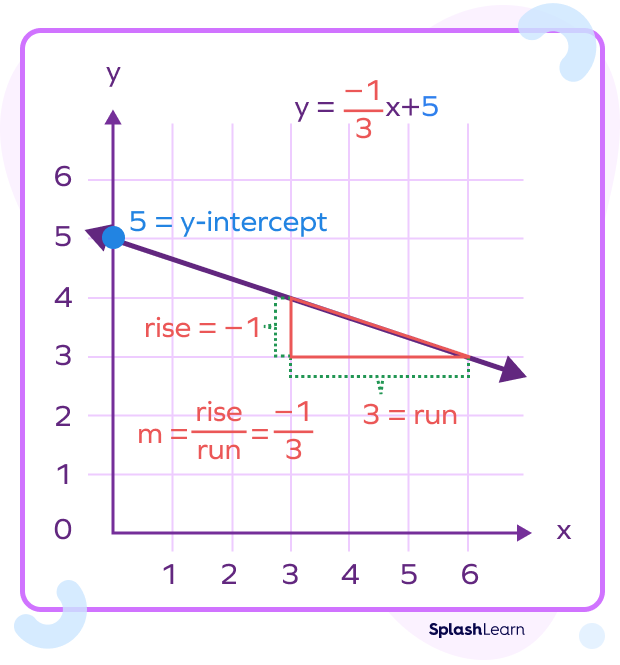
Example 2: Here, the line $y = \frac{-1}{3}x + 5$ has the rise over run ratio equal to $\frac{-1}{3}$. 

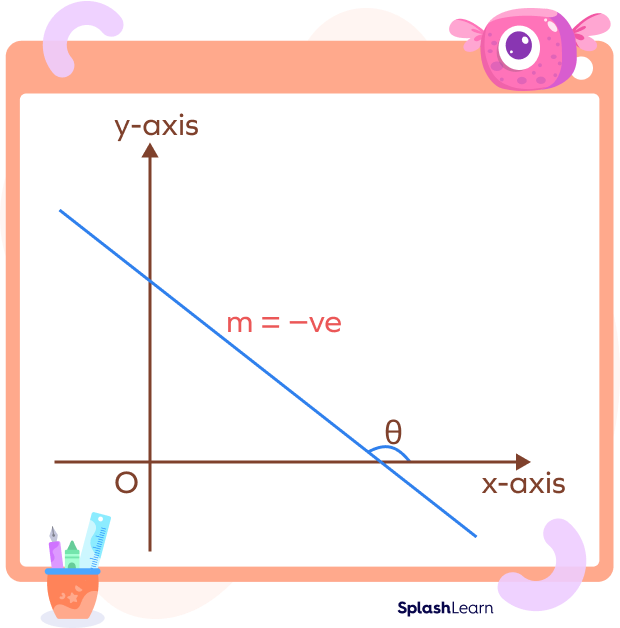
Negative Slope Graph

A line with a negative slope goes downward as we move in the positive direction of the x-axis. Mathematically, it means that as x increases, y decreases. 

So, what does a negative slope look like? Take a look at the blue line shown below.

You can see that the blue line is trending downwards as it moves from left to right.

How to Calculate Negative Slope

Let’s discuss methods to calculate negative slope.

Method (i)

When the coordinates of two points on the line are given, we can use this method.

Example: A line passes through points (4,2) and (3,5). To find if the line has a negative slope, we can use the slope formula.

Let us assume $(x_1,\;y_1) = (4,\;2)$ and $(x_2,\;y_2) = (3,\;5)$

Slope(m) $= \frac{y_2\;-\;y_1}{x_2\;-\;x_1}$

Then we have $m = \frac{5 \;-\; 2}{3 \;-\; 4} = \frac{3}{-\;1} = -\;3$

Since m has a negative value, the line passing through points (4,2) and (3,5) has a negative slope.

Method (ii)

If the equation of a line is of the form $ax + by = c$, then we can use this method.

Example: The equation of a line is $2x + 3y = 5$

We can rewrite the equation as $y = \frac{-\;2}{3} x + \frac{5}{3}$

If we equate the above equation with the general equation of the line in the slope-intercept form, which is $y = mx + c$ (here in the equation, m is the slope of the line, and c is the intercept made by the line with the x-axis)

Comparing the equation $y = \frac{-\;2}{3} x + \frac{5}{3}$ with $y = mx + c$, we get

We get $m = \frac{-2}{3}$ 

Since m has a negative value, the line $2x + 3y = 5$ has a negative slope.

Method (iii)

If the angle made by the line with the x-axis is given, then we can use this method.

Example: If a line makes an angle of 135 degrees with the positive direction of the x-axis then to find the negative slope, we use the slope formula.

Since the line makes an angle of 135 degrees with the positive direction of the x-axis, the slope of that line will be

$m = tan\; 135^\circ = tan\; (90 + 45) = -\;tan\; (45)= \;-1$

Thus, the given line has a negative slope. 

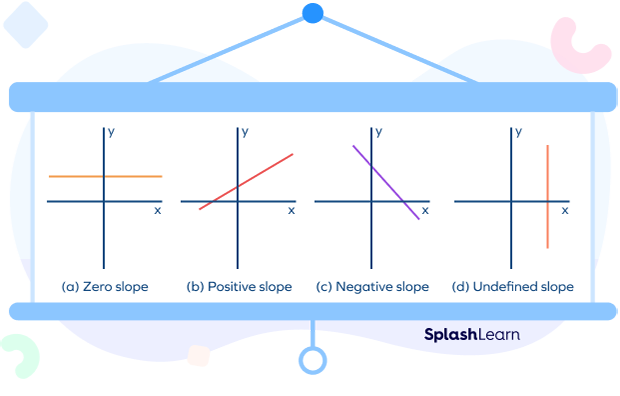
Types of Slope

There are four types of slope.

1. Positive slope: A line that makes an acute angle with the positive direction of the x-axis has a positive slope. The line with a positive slope rises up as we move from left to right.
   
2. Negative Slope: A line that makes an obtuse angle with the positive x-axis has a negative slope. The line with a negative slope sinks down as we move from left to right.
   
3. Zero slopes: A line that makes an angle of 0 degrees with the positive x-axis has zero slope. The line with zero slope does not have a rise, it remains horizontal, parallel to the x-axis.
   
4. Undefined slope: A line that makes 90 degrees with the positive x-axis has an undefined slope. The line with an undefined slope is a vertical line or a line parallel to the y-axis.

Facts about Negative Slope

Conclusion

In this article, we learned about the negative slope and properties of lines having a negative slope. Let’s solve a few examples and practice problems based on these concepts.

Solved Examples on Negative Slope

1. Find whether the line passing through the points (5,2) and (2,-5) has a negative slope.

Solution: 

We have the slope formula

 Slope$(m) = \frac{y_2\;-\;y_1}{x_2\;-\;x_1}$

Let us assume $(x_1,\;y_1) = (5,\;2)$ and $(x_2,\;y_2) = (2,\;-5)$

Now, we have to find $y_2\;-\;y_1 = (\;-5)\;-2 = \;-7$

Again, we are to find $x_2\;-\;x_1 = 2\;-\;5 = \;-3$

Now using the formula, Slope$(m) = \frac{y_2\;-\;y_1}{x_2\;-\;x_1} =\frac{-7}{-3} = \frac{7}{3}$

Since the value of the slope(m) is positive, the line passing through the points (5,2) and (2,-5) does not have a negative slope.

2. Show that the line with equation $5x + 2y = 5$ has a negative slope.

Solution: 

The equation of a line is given as $5x + 2y = 5$.

$2y = -\; 5x + 5$

$y = \frac{-\;5}{2} x + \frac{5}{2}$

Rewriting the equation as $y = \frac{-\;5}{2}x + \frac{5}{2}$ to compare it with the general form of a line in slope-intercept form, which is $y = m x + c$.

Hence, we get the value of $m = \frac{-5}{2}$ which is a negative number.

So, the line  $5x + 2y = 5$ has a negative slope.

3. Show that the line that makes an angle of 60 degrees with the positive direction of the x-axis does not have a negative slope.

Solution: 

We have a formula of slope(m) $= tan\; \theta$; here$\theta$ is the angle made by the line with the positive direction of the x-axis.

It is given that the line makes an angle of 60 degrees with the positive direction of the x-axis.

Hence, slope(m) $= \tan\;60^\circ = \sqrt{3}$, which is a positive value.

Therefore, the line with an angle of 60 degrees along the positive direction of the x-axis does not have a negative slope.

4. Show that the line that makes an angle of 150 degrees with the positive direction of the x-axis has a negative slope.

Solution: We have a formula of slope(m) $= tan\; \theta$; here $\theta$ is the angle made by the line with the positive direction of the x-axis.

It is given in the question that the line makes an angle of 150 degrees with the positive direction of the x-axis.

Hence, slope$(m) = tan\; 150^\circ = tan\;(90 + 60) =\;-\frac{1}{3}$, which is a negative value.

Therefore the line with an angle of 150 degrees along the positive direction of the x-axis has a negative slope.

Practice Problems on Negative Slope

Frequently Asked Questions on Negative Slope