What Are Benchmark Numbers?
A benchmark is defined as the standard or reference point based on which other things can be measured, or assessed, or compared. So, what is a benchmark in math? What does benchmark mean in math?
Benchmark numbers are numbers using which other numbers or quantities can be estimated and compared. Benchmark numbers are usually multiples of 10 or 100, and sometimes multiples of 25. They are used to simplify the operations such as addition, subtraction, etc.
Here are some examples of benchmark numbers.

Recommended Games
Definition of Benchmark Numbers
Benchmark numbers are numbers that are easy to add, subtract, multiply or divide.
Any multiple of 10, 100, or multiples of 25 is considered as a benchmark number.
Benchmark numbers are also known as “friendly” numbers.
Examples: 10, 50, 1000, 80, 5000
A benchmark number is usually a multiple of 10, 100, 1000, etc., or a number having 0 at the ones place or any other decade number, such as 1, 20, 30, 40, etc.
Let’s take a look at examples and non-examples of benchmark numbers.
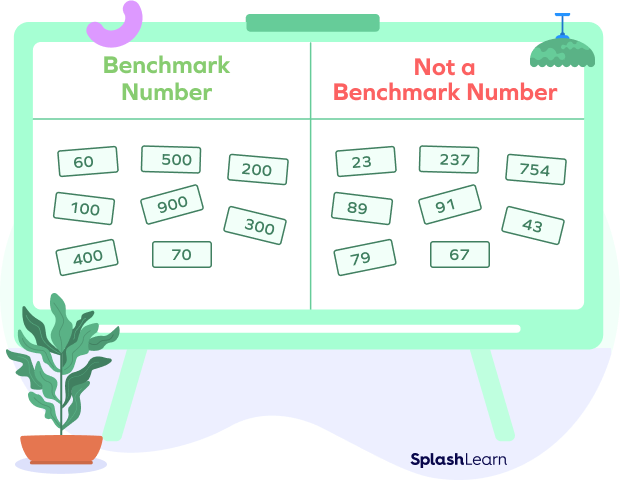
Note: The most important benchmark numbers for young learners are 5 and 10. Because the number 10 plays such a huge role in our number system, and because $5 + 5 = 10$, it is very useful to develop relationships between the numbers 1 to 10.
Recommended Worksheets
List of Some Common Benchmark Numbers

Benchmark Numbers on a Number Line
Benchmark numbers help us to locate numbers, compare numbers. The following image shows benchmark numbers on the number line when counting by 1, 100, and 1000. Identify the benchmark numbers and locate any point on the number line.
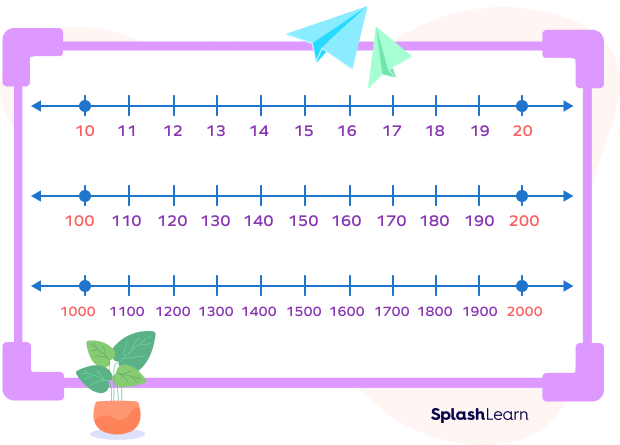
Let’s understand benchmark numbers on a number line with examples.
1. Show benchmark numbers of 43 when counting by 10 on a number line.
The benchmark numbers of 43, when counting by 10, include 40 and 50. Observe the number line below to know how to locate 43 between its two benchmark numbers on the number line.

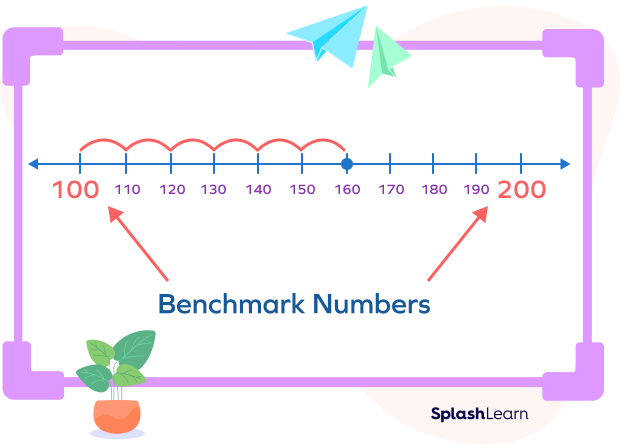
2. Show benchmark numbers of 160 when counting by 100 on a number line.
The benchmark numbers of 160 when counting by 100 include 100 and 200. Observe the number line below to know how to locate 160 between its two benchmark numbers on the number line. Notice that 160 itself is a benchmark number!
Addition Using Benchmark Numbers
Benchmark numbers make addition strategies simple. When adding two or more numbers, try to reach a benchmark number!
Let’s see how!
Example 1: $34 + 57 + 31 + 9$
Let’s break down this problem to reach benchmark numbers.
$34 + 57 + 31 + 9 = 30 + 4 + 50 + 7 + 30 + 1 + 9$
$= 110 + 11 + 10$
$= 130 + 1$
$= 131$
Refer to the following chart to reach the benchmark numbers faster. These number pairs make tens.

You can also use them to make multiples of ten or even “hundreds” or “thousands.”
For example, if $2 + 8 = 10$, then
$22 + 8 = 30$
$20 + 80 = 100$
$200 + 800 = 1000$
There are many such combinations you can make!
Estimation Using Benchmark Numbers
Since the benchmark numbers are easy to add, subtract, multiply or divide easily, we can use them for estimation where some error in calculation is allowed.
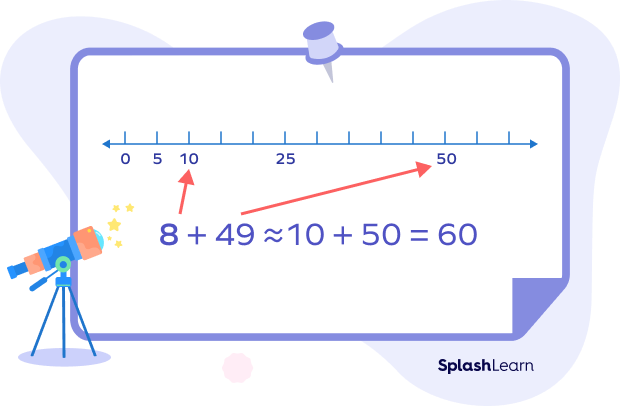
Example 1: Estimating addition using benchmark numbers
Example 2: $31 \times 11 \approx 30 \times 10 \approx 300$
Let’s Sing!
When there are big numbers to compare,
Don’t let them give you a scare!
Bring in the benchmarks, to be fair!
Conclusion
In this article we studied benchmark numbers. A benchmark number is any multiple of 10, 100, 1000, and sometimes 25 against which other numbers or quantities can be compared or accessed.
Solved Examples on Benchmark Numbers
- Identify the benchmark numbers: 43, 90, 100, 76, 500, 300
Solution:
Benchmark numbers in the given list are 90, 100, 500, 300.
- How to solve $54 + 32 + 67 + 13$ using benchmark numbers?
Solution:
Club the number pairs which make benchmark numbers or multiples of tens.
$54 + 32 + 67 + 13 = 50 + 4 + 30 + 2 + 60 + 7 + 10 + 3$
$= 150 + 16$
$= 166$
- Which numbers should be added to the following numbers to get a benchmark number?
- 4 b) 35 c) 313 d) 999
Solution:
Benchmark numbers are usually multiples of 10 or numbers having “0” at the ones place.
- $4 + 6 = 10$
- $35 + 5 = 40$
- $313 + 7 = 320$
- $999 + 1 = 1000$
Practice Problems on Benchmark Numbers
Benchmark Numbers: Definition with Examples
When looking at the tens place, the number 18 comes between which two benchmark numbers?
18 comes between two benchmark numbers, 10 and 20.
Which number comes between the benchmark numbers 80 and 90?
The numbers lying between the benchmarks 80 and 90 are:
81, 82, 83, 84, 85, 86, 87, 88, 89
When looking at the hundreds place, the number 462 comes between which two benchmark numbers?
The hundred place benchmark of 462 is 400 and 500.
Which number pair makes a benchmark number?
$101 + 99 = 100 + 1 + 99 = 200$
What numbers come between the benchmark numbers 3500 and 3600?
$3599 = 3500 + 90 + 9$
So, it lies between 3500 and 3600.
Frequently Asked Questions on Benchmark Numbers
Why is the benchmark number used in mathematics?
Benchmark numbers are used as a point of reference based on which we can compare different numbers. They make calculations easier.
What is the reason behind which the benchmark number is called a friendly number?
Since benchmark numbers make calculations easier and also they make calculations easier, they are called friendly numbers.
What is the difference between benchmark number and benchmark fraction?
A benchmark number is a number that is used as a reference point whereas a benchmark fraction is a fraction that is used as a reference point. For example, 10 is a benchmark number, whereas $\frac{1}{2}$ is a benchmark fraction.
Give two examples of benchmark number and benchmark fraction
Example for benchmark numbers: 10, 100
Example for benchmark fractions: $\frac{1}{2},\; \frac{1}{4}$
What is the need for a benchmark number?
Benchmark, according to the Oxford Dictionary, means “something that can be measured and used as a standard that other things can be compared with.” It’s a part of math. They make calculations easy.




































