Open Interval and Closed Interval – Definition, Examples, FAQs

What Is Open Interval and Closed Interval?

There are two types of intervals known as open interval and closed interval. In an open interval (a, b), the endpoints are not included. In a closed interval [a, b], the endpoints are included. 

Before we dive into the details of open intervals and closed intervals, let us first understand the definition of interval in math. 

What Is an Open Interval?

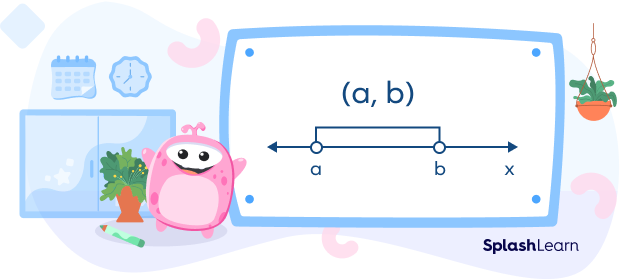
An interval in which the endpoints are not included is called an open interval. An open interval (a, b) represents the set of all real numbers x such that a $\lt x \lt b$.

We get an open interval if an inequality has the signs

• less than $\lt$
• greater than $\gt$

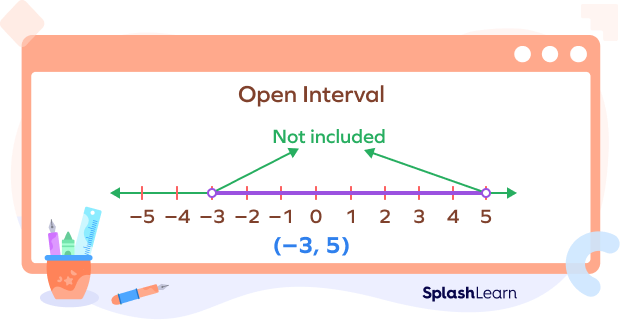
Example: (-3, 5) is an open interval that includes all the real numbers greater than -3 but less than 5. We can write is with the help of compound inequality $\;-\;3 \lt x \lt 5$. In the set notation, we can express the open interval $(\;-\;3,\; 5)$ as $\left\{ x | \;-\;3 \lt x \lt 5\right\}$.

Open Interval Notation

A round bracket or parentheses ( ) is used to denote an open interval. An open interval is written as an ordered pair within round brackets as (a, b). 

Open Interval on a Number Line

To represent an open interval on a number line, we use two hollow circles to denote the endpoints. These hollow circles show that the points are not included.

Open interval (-3, 5) on a number line:

What Is a Closed Interval?

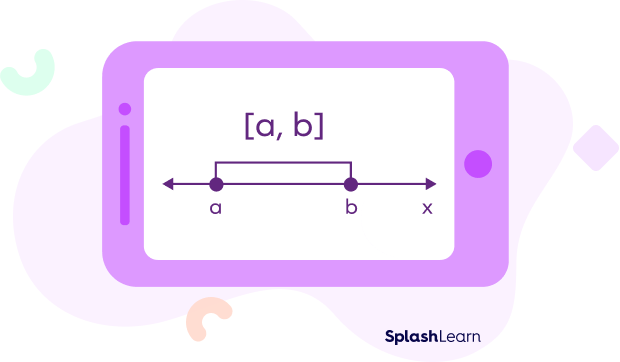
An interval in which the endpoints are included is called a closed interval. A closed interval [a, b] represents the set of all real numbers x such that $a\le x \le b$.

We get closed interval if an inequality has the signs

• less than or equal to $\le$
• greater than or equal to $\ge$

Example: $\left[2, 7\right]$ is a closed interval which includes 2, 7 and all the real numbers between 2 and 7. We can write it with the help of compound inequality $2 \le x \le 7$. In the set notation, we can express the open interval $\left[2, 7\right]$ as $\left\{ x | 2 \le x \le 7\right\}$.

Closed Interval Notation

Square brackets $\left[ \right]$ are used to denote a closed interval. We write a closed interval as an ordered pair within square brackets as $\left[a,\; b\right]$.

Closed Interval on a Number Line

To represent a closed interval on a number line, we use two solid circles to denote the endpoints. Solid circles convey that these points are to be included.

Closed interval [2, 7] on a number line:

What Is the Difference between Open Interval and Closed Interval?

Open Interval vs. Closed Interval
Open Interval	Closed interval
Open intervals are denoted by an ordered pair (a, b) with round brackets or parentheses ( ).	Closed intervals are denoted by an ordered pair [a, b] with square brackets [ ].
Endpoints a and b are not included.	Endpoints a and b are also included.
Open interval (a, b) can be defined by an inequality $a \lt x \gt b$.	Closed interval [a, b] can be defined by an inequality $a \le x \ge b$.
Endpoints are denoted by hollow circles on a number line.	Endpoints are denoted by solid circles on a number line.

Operations on Open Intervals and Closed Intervals

Let’s discuss two operations on intervals that are similar to the operations we perform on sets.

Union of Two Intervals

The union of two intervals A and B included all the elements that are in A, in B, or both in A and B.

Examples: 

$(1, 5) (2, 7) = (1, 7)$

$\left[4, 9\right] (5, 15) = \left[4, 15\right)$

Intersection of Two Intervals

The intersection of two intervals is the collection of all the elements that are common to both the intervals.

Examples:

$(1, 5) (2, 7) = (2, 5)$

$\left[4, 9\right] (5, 15) = (5, 9)$

Complement of an Interval

The complement of an interval with respect to the set of real numbers is the set of all real numbers that are not in the given interval.

Example: $A = (4, 8)$

Complement of $A = A’ = (-,4] [8,)$

Facts about Open Interval and Closed Interval

Conclusion

In this article, we learned about open and closed intervals, definitions, notations along with operations on them. Let’s solve a few examples and practice problems based on these concepts to understand the concept better.

Solved Examples on Open Interval and Closed Interval

1. Look at the two intervals $\left[3, 7\right]$ and $(2, 6)$. Which interval includes the number 3? Which interval includes 6?

Solution: 

The closed interval $\left[3, 7\right]$ includes all the real numbers between 3 and 7, including both 3 and 7.  The open interval (2, 6) includes all the real numbers greater than 2 but less than 6. 

Both intervals include the number 3. 

The closed interval $\left[3, 7\right]$ includes the number 6. 

The open interval (2, 6) does not include 6. 

2. Write the given inequalities as intervals.

i) $0 \lt x \lt 99$

i) $\;-\;5 \le x \le 8$

Solution: 

i) $0 \lt x \lt 99$

Endpoints are not included. So, we use an open interval.

The inequality can be written as (0,99).

ii) $\;-\;5 \le x \le 8$

Endpoints are included. So, we use a closed interval.

The inequality can be written as $\left[\;-5,\;8\right]$.

3. What is the union and intersection of the intervals $(0,\; 99)$ and $[1,\; 100]$?

Solution: 

$(0,\; 99)$ represents the inequality $0 \lt x \lt 99$.

$\left[1,\; 100\right]$ represents the inequality  $1 \le x \le 100$.

The union of intervals includes the elements present in either of the intervals.

$(0,\; 99) \cup \left[1,\; 100\right] = \left(0,\; 100\right]$

The intersection includes the elements common to both intervals.

$(0,\; 99) \cap \left[1,\; 100\right] = \left[1,\; 99\right)$

4. Observe at the inequality $\;-\;4 \lt x \lt 3$ and state if it is an open interval or a closed interval. Represent it on a number line.

Solution: 

The inequality is $\;-\;4 \lt x \lt 3$ is an open interval. This means x is less than 3 but greater than -4. Here, as  -4 and 3 are not included, it is an open interval.

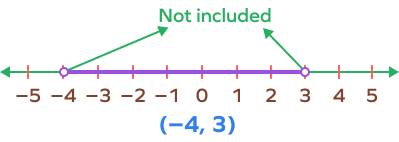
Practice Problems on Open Interval and Closed Interval

Frequently Asked Questions on Open Interval and Closed Interval