Interval in Math

Imagine if you had to sit in class continually without a recess or lunch break. What would that be like?
Most things cannot go on without break. There is usually a gap that comes in between. These gaps are known as intervals.
Did you know there are intervals in math as well? They help us measure these gaps in terms of numbers. Let’s understand what is an interval in math in detail.
Recommended Games
What is an Interval in Math?
Let’s look at the definition of interval in Math.
An interval is a gap between two things or points. Let’s understand this better.
How are these two lines different?
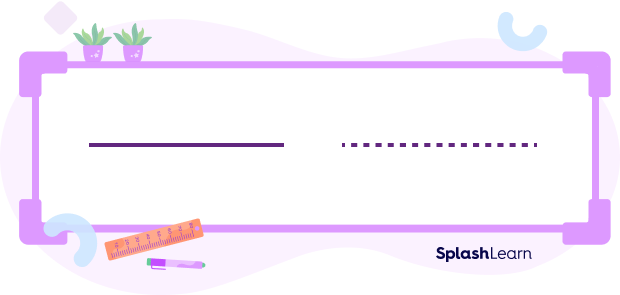
The first line is continuous, and the second line has gaps.
What is the difference between the emergency flashing light of an ambulance and its headlamp?

The headlamps flash continuously. However, the emergency flashing lights flash at intervals. Continuous means without any gap whereas interval means with gaps.
Let us see another example to understand intervals:
When a car moves on the road, it has to stop when the traffic light flashes red. However, if the traffic light is green, the car would continue moving without having to stop.

Recommended Worksheets
Interval in Math
An interval in math is measured in terms of numbers. An interval includes all the numbers that come between two particular numbers.
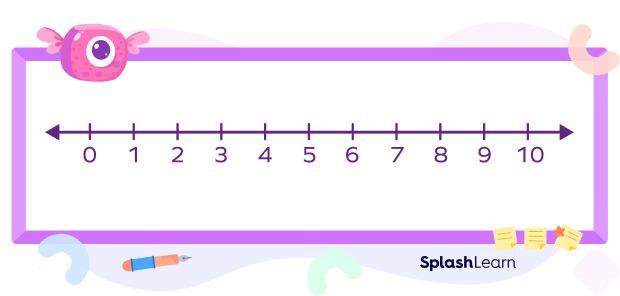
This range includes all the real numbers between those two numbers. Real numbers are any kind of number you can think of.
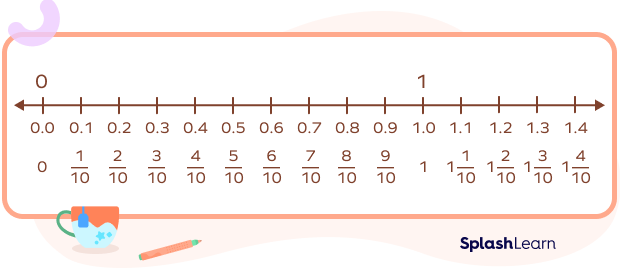
For example, an interval between 0 and 10 would include not just 1, 2, 3, 4, 5, 6, 7, 8, and 9 but also the other kinds of numbers between them. These would include decimal numbers like 1.3 and fractions like 1/10 as well.
Interval Notation
Interval notation is a simplified way of describing a particular interval. Let’s see how it’s done.
Step 1: We write the first and last number of the interval, which are the endpoints of the interval. For example, if the interval is from 6 to 20, we write 6, 20.
Step 2: We use a round or square bracket on each side of the two numbers. We use:
- A square bracket [ ], if we want to include the endpoints
- A round bracket ( ), if we don’t want to include the endpoints
So in this example, we use:
- [6, 20] if the interval includes 6 and 20
- (6, 20) if the interval excludes 6 and 20
- (6, 20] if the interval excludes 6 but includes 20
- [6, 20) if the interval includes 6 but excludes 20
Types of Intervals in Math
So, we can see that some intervals include the endpoints, some partially include them, and some do not include them. Based on this, there are three types of intervals in math.
These are:
- Open interval
- Closed interval
- Half-open and half-closed interval
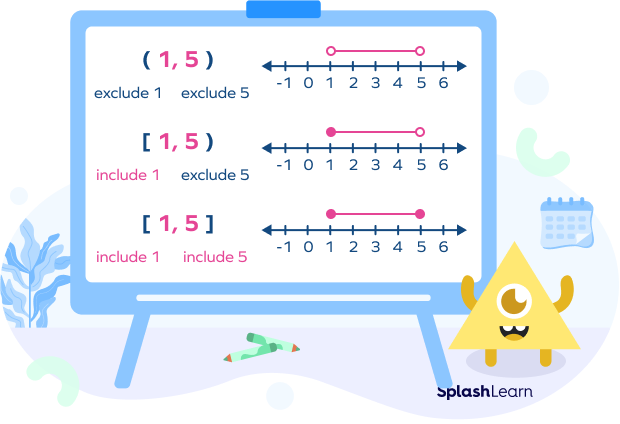
Open Interval
This type of interval does not include the endpoints. For example, (5, 10) does not include endpoints 5 and 10.
Closed Interval
This type of interval includes the endpoints. For example, [4, 9] includes the endpoints 4 and 9.
Half-Open and Half-Closed Interval
This type of interval includes only one of the endpoints.
For example, (6, 16] includes 16 but does not include 6, whereas [6,16) includes 6 but does not include 16.
This is what the different types of intervals look like on number lines:
Time Interval
Let us learn what a time interval is.
Suppose you are walking from your home to your school. You walk continually and reach school in 10 minutes.
Now, while walking back home, you get tired and decide to sit for 2 minutes. You stop for 2 minutes and then start walking home again. So, we say you took a time interval of 2 minutes while walking back home.
The time interval can be defined as the time between two events.
We can show time intervals on a timeline:
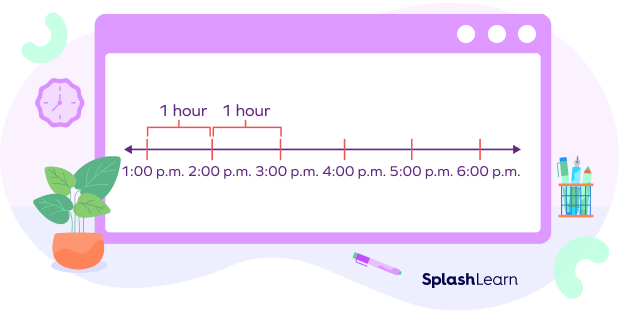
Here, the timeline shows intervals of 1 hour. We can find the time between events using intervals.
For example, Sam started playing soccer at 4:30 p.m. He finished the game at 6:00 p.m. For how long did he play?
We can draw a timeline as follows:
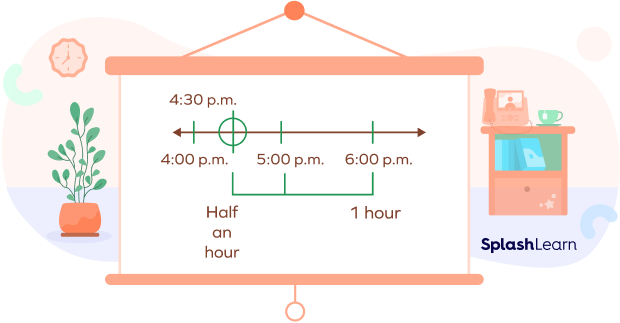
The interval from 4:30 p.m. to 5:00 p.m. is half an hour. Then, from 5:00 p.m. to 6:00 p.m. is an hour. So, that makes it an hour and a half. Sam played soccer for one and a half hours.
Fun Facts
- The word interval is derived from Latin “Inter” meaning “between” and “vallum” meaning “space between ramparts”, i.e., the space between protective walls of a castle.
Solved Examples
Example 1. What is the interval between 2 p.m. and 6:45 p.m.?
Solution: Let’s subtract the time values:
6:45 – 2:00 = 4:45
Thus, there are 4 hours and 45 minutes between 2 p.m. and 6:45 p.m.
So the interval will be 4 hours and 45 minutes.
Example 2. Students between the age of 12 and 17 can be on the school soccer team. Give an interval that will represent this information.
Solution. The permitted ages are between age 12 to age 17.
So, the interval is [12, 17].
Example 3: To pass a math exam, students need to score above 65 marks out of a total of 100. How will this be represented as an interval?
Solution. The students need to score above 65 marks and up to 100 marks.
The interval for this will be written as (65, 100].
Practice Problems
Interval in Math
For a class to take place, there need to be at least 10 students present out of a total of 40 students in the class. Represent this as an interval.
There need to be a minimum of 10 students present, and the maximum number of students that can be present is 40. So, the interval is [10, 40].
A sports competition requires the total number of participants from a school to be less than 30. However, there should be a minimum of 12 participants from the school. Represent this as an interval.
The minimum number of participants required is 12, so 12 is included. The maximum number of participants must be less than 30, so 30 is not included. Therefore, the interval is [12, 30).
While going from 2 to 3:25 on a clock, what is the interval covered by the minute hand?
We know that the interval between 2 and 3:25 on a clock is 1 hour and 25 minutes or 85 minutes. So the minute hand covers an interval of 85 minutes.
Your mom is driving and stops at a traffic light that has just turned red. The light stays red for 2 minutes. Then, it turns green, and she drives ahead. What is the interval of the red light?
The traffic light stays red for 2 minutes, so she stops for 2 minutes. The interval of the red light is 2 minutes.
Frequently Asked Questions
Can an interval be measured in fractions or decimals?
Yes, an interval can be measured in fractions or decimals because they are real numbers. For example, 17 minutes, 0.5 second, ¼ of an hour, etc. Time intervals, however, cannot be negative.
What units are used to measure time intervals?
Units like seconds, minutes, hours, days, months, years, etc., are used to measure time intervals.
Can you measure a distance between two points as an interval?
Yes, you can, because it will be a range between two numbers measuring in inches, feet, yards, or miles.




































