Perfect Squares – Definition, Formula, List, Examples

What Are Perfect Squares?

A number expressed as a product of an integer by itself is called a perfect square. Since the same number is multiplied twice, the perfect square is also written as the second exponent of an integer. Thus, the squares of all integers are known as perfect squares.

Example: 16 is a perfect square since it is a product of an integer with itself.

$4 \times 4 = 16$

Also, the product $(-\;4)$ with $(-\;4)$ gives 16.

$(-\;4) \times (-\;4) = 16$

Notice that the squares of 4 and $-4$ are the same. 

Perfect Squares: Definition

The definition of perfect squares in math can be given as the positive integers obtained by multiplying an integer with itself.

To find a perfect square, simply multiply any integer by itself!

How to denote a perfect square? We write “2” as the power of the given number.

We read $5^2$ as “five squared.”

Examples of Perfect Squares

Here are a few examples of perfect squares.

$1^2 =$	1
$2^2 =$	4
$3^2 =$	9
$4^2 =$	16
$5^2 =$	25
$6^2 =$	36
$7^2 =$	49
$8^2 =$	64
$9^2 =$	81
$10^2 =$	100

Let’s consider the visual representation. Perfect squares can be represented in the shape of a square. In other words, you can represent them in equal numbers of rows and columns in a multiplication array.

Example: Suppose you have 4 marbles. You can arrange them in 2 rows and 2 columns such that they will fit in a square shape. Similarly, you can arrange 9 marbles in a square shape using 3 rows and 3 columns. 

Non Examples of Perfect Squares

If you take 6 marbles, you can either arrange them in an array of 2 rows and 3 columns, or 3 rows and 2 columns. Now that the number of rows and columns are different, the number 6 cannot be a perfect square number.

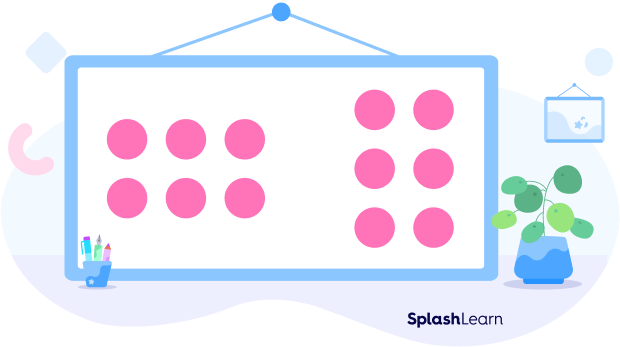
Perfect Squares: Formula

Since perfect squares are numbers that can be expressed as a product of an integer with itself which ultimately gives us the square of that integer. The perfect squares formula can be expressed as:

$P = n \times n = n^2$  

where P denotes a perfect square number and n denotes an integer.

Perfect Square Numbers

Perfect square numbers are positive integers that correspond to the multiplication of two of the same integers with themselves. It can also be that if you take the root of a perfect square number, you will only get a whole number. Below is a perfect squares list of the first 100 natural numbers.

Perfect Squares Chart (From 1 to 100)

Perfect Squares from 1 to 100
$1 \times 1$	$1^2$	1
$2 \times 2$	$2^2$	4
$3 \times 3$	$3^2$	9
$4 \times 4$	$4^2$	16
$5 \times 5$	$5^2$	25
$6 \times 6$	$6^2$	36
$7 \times 7$	$7^2$	49
$8 \times 8$	$8^2$	64
$9 \times 9$	$9^2$	81
$10 \times 10$	$10^2$	100

Perfect Squares List

$1^2 = 1$	$2^2 = 4$	$3^2 = 9$	$4^2 = 16$	$5^2 = 25$	$6^2 = 36$	$7^2 = 49$	$8^2 = 64$	$9^2 =81$	$10^2 = 100$
$11^2 = 121$	$12^2 = 144$	$13^2 = 169$	$14^2 = 196$	$15^2 = 225$	$16^2 = 256$	$17^2 = 289$	$18^2 = 324$	$19^2 = 361$	$20^2 = 400$
$21^2 = 441$	$22^2 = 484$	$23^2 = 529$	$24^2 = 576$	$25^2 = 625$	$26^2 = 676$	$27^2 = 729$	$28^2 = 784$	$29^2 = 841$	$30^2 = 900$
$31^2 = 961$	$32^2 = 1024$	$33^2 = 1089$	$34^2 = 1156$	$35^2 = 1225$	$36^2 = 1296$	$37^2 = 1369$	$38^2 = 1444$	$39^2 = 1521$	$40^2 = 1600$
$41^2 = 1681$	$42^2 = 1764$	$43^2 = 1849$	$44^2 = 1836$	$45^2 = 2025$	$46^2 = 2116$	$47^2 = 2209$	$48^2 = 2304$	$49^2 = 2401$	$50^2 = 2500$
$51^2 = 2601$	$52^2 = 2704$	$53^2 = 2809$	$54^2 = 2916$	$55^2 = 3025$	$56^2 = 3136$	$57^2 = 3249$	$58^2 = 3364$	$59^2 = 3481$	$60^2 = 3600$
$61^2 = 3721$	$62^2 = 3844$	$63^2 = 3969$	$64^2 = 4096$	$65^2 = 4225$	$66^2 = 4356$	$67^2 = 4489$	$68^2 = 4624$	$69^2 = 4761$	$70^2 = 4900$
$71^2 = 5041$	$72^2 = 5184$	$73^2 = 5329$	$74^2 = 5476$	$75^2 = 5625$	$76^2 = 5776$	$77^2 = 5929$	$78^2 = 6084$	$79^2 = 6241$	$80^2 = 6400$
$81^2 = 6561$	$82^2 = 6724$	$83^2 = 6889$	$84^2 = 7056$	$85^2 = 7225$	$86^2 = 7396$	$87^2 = 7569$	$88^2 = 7744$	$89^2 = 7921$	$90^2 = 8100$
$91^2 = 8281$	$92^2 = 8464$	$93^2 = 8649$	$94^2 = 8836$	$95^2 = 9025$	$96^2 = 9216$	$97^2 = 9409$	$98^2 = 9604$	$99^2 = 9801$	$100^2 = 10000$

How to Identify Perfect Squares

To identify perfect squares, we mostly have to pay attention to the last digit of the number. 

In the chart, we see that the integers 1, 2, 7, 8 never appear at the ones place. The ones place has the numbers 0, 1, 4, 5, 6, or 9. 

We can deduce that numbers with 00, 1, 4, 5, 6, 9 as their last digit can be perfect squares. So, if the last digit is 2, 3, 7, or 8, the given number is not a perfect square.

Here are some other observations you can make!

1. Perfect squares of numbers ending with 3 or 7 have 9 at their ones place. 
2. Perfect squares of numbers ending with 5 have 5 at their ones place.
3. Perfect squares of numbers ending with 4 or 6 have 6 at their ones place.
4. Perfect squares of numbers ending with 2 or 8 have 4 at their ones place.
5. Perfect squares of numbers ending with 1 and 9 have 1 at their ones place.

In summary, here are some ‘perfect square rules’ or tests you can apply to identify a perfect square.

1. All perfect squares end in 1, 4, 5, 6, 9 or 00 (even number of zeros). Thus, a number that ends in 2, 3, 7 or 8 is not a perfect square.

2. No number can be a perfect square unless its digital root is 1, 4, 7, or 9.

3. Total numbers of prime factors of a perfect square are always odd.

4. If the unit digit ends in 5, tens digit is always 2.

5. If a number ends with zero, you may look at how many zeroes are at the end. If the number of zeroes is odd, the number isn’t a perfect square. If the number of zeroes is even, then it might be a perfect square. 

For example, 1000 has an odd number of zeroes, so it is not a perfect square number. 

$400 = 20^2$ … a perfect square

300 … not a perfect square

Identify Perfect Squares Using the Square Root

One other way to check if a number is a perfect square is by finding out the square root of the number. The integer that is multiplied with itself to find the perfect square is called the “square root” of the perfect square.

For example, 4 and $-4$ are square roots of 16.

• If the square root comes out to be an integer, then the given number is a perfect square. 
• If the square root comes out to be a decimal number, then the given number is not a perfect square number. 

Example 1: $\sqrt{24} = 4.89$, which is not an integer. Thus, 24 is not a perfect square.

Example 2: $\sqrt{49} = \pm\; 7$, which is an integer. Thus, 49 is a perfect square.

Tips and Tricks to Find Perfect Squares

Sometimes, we can find perfect squares of some numbers without using the long multiplication method.

Example 1: Numbers ending with the digit 5

Separate the two digits of the number. Take the tens place digit and multiply it by its successor. Square the unit place digit. Write these two results together. $75^2 = 5625$.

Example 2: Using the formula $(a + b)^2 = a^2 + 2ab + b^2$

To find the square of large numbers, you can split them into friendly numbers using the above formula and then expand.

$67^2 = (60 + 7)^2 = 60^2 + 2(60)(7) + 7^2$ 

      $= 3600 + 840 + 49$

    $= 4489$

Facts about Perfect Squares

• If a number has zero at the ones place, then the square of the number will always have even numbers of zeros at the end. 
• Square roots of negative numbers are undefined. There doesn’t exist any negative perfect square numbers.
• The area of the geometric shape “square” having side “s” is given by $s \times s = s^2$.
• The principal square root of a number is the positive square root. Usually, “the square root” of a number refers only to the principal square root or the positive root.

Conclusion

In this article, we discussed the concept of perfect squares and learned how to identify them. We also discussed the definition of a perfect square, formula to find the perfect square. Let’s solve a few examples for better understanding.

Solved Examples on Perfect Squares

1. Find the perfect square of 13 using the formula $(a + b)^2 = a^2 + 2ab + b^2$.

Solution: 

We will split 13 as $(10 + 3)$ to use the formula.

$13 \times 13 = 13^2$

     $= (10 + 3)^2\; …(a+b)^2$

     $= 100 + 60 + 9\; …(a + b)^2 = a^2 + 2ab + b^2$

     $= 169$

2. Determine if 3600 is a perfect square or not.

Solution: 

Since 3600 ends with two zeros, it is likely that 3600 is a perfect square number. Factoring 3600 gives us the following expression:

$3600 = 6 \times 6 \times 10 \times 10 = 60 \times 60$, which satisfies the condition of perfect square numbers. So, 3600 is a perfect square number.

4. What is the smallest whole number to be added to 55 to make it a perfect square?

Solution: 

The next closest perfect square number to 55 is 64, which is the perfect square of 8. 

$64\;-\;55 = 9$

If we add 9 to 55, we will get 64, which is a perfect square number.

Practice Problems on Perfect Squares

Frequently Asked Questions on Perfect Squares