Solving Radical Equations: Steps, Definition, Examples

What Are Radical Equations?

Radical equations are equations in which a variable is under a radical symbol.

Before we explore the concept of radical equations, let’s quickly take a look at the important terminologies that will be helpful.

Radical symbol: The symbol “⎷” that we use to denote square root, cube root, or nth root (like $\sqrt{},\; ^3\sqrt{},\; ^4\sqrt{}$, etc.) is called a “radical symbol.”  

The horizontal line at the top is called the vinculum.

In the radical symbol, $(\sqrt{}$ or $^2\sqrt{}),\; ^3\sqrt{},\; ^4\sqrt{}$, etc., the numbers 2, 3, and 4 written in the little dent represent the “index.”

If the index is not written, it is considered to be 2.

Radical expression: A radical expression is the expression that has an n^th root (usually a square root).

Radicand: A number or expression inside the radical symbol.

Important Note: The square root of a number in an exponent form is the number raised to the power of $\frac{1}{2}$.

$\sqrt{x} = x^\frac{1}{2}$

The n^th root of x can be written as $^n\sqrt{x} = x^\frac{1}{n}$.

The n^th root of xm can be written as $^n\sqrt{x}^m = x^\frac{m}{n}$

Examples: $^3\sqrt{x^2} = (x^2)\frac{1}{3} = x^\frac{2}{3}$

       $^3\sqrt{x^4} = x^\frac{4}{3}$

      $^2\sqrt{x^5} = x^\frac{5}{2}$ etc.

Radical Equations Definition

A radical equation is an equation in which a variable is in the radicand of the expression. 

At least one radical sign of a radical equation includes a variable. 

In other words, a radical equation has a variable with a rational exponent. 

Examples of Radical Equations: $\sqrt{a} + 4 = 13,\; \sqrt{x\;-\;1} = 5$ 

How to Solve Radical Equations

Solving a radical equation simply means finding the value of the variable. The variable in a radical equation is under the radical sign. Thus, exponent rules and fundamental algebraic principles must be followed in order to solve radical equations. A square root can be eliminated by squaring, and cube roots can be eliminated by cubing, etc. 

Note that the solutions obtained by solving a radical equation must be verified.

The binomial square formulas are extremely useful when solving a radical equation where a binomial term is present on one side of the radical equation.

• $(a + b)^2 = a^2 + 2ab + b^2$
• $(a\;-\;b)^2 = a^2\;-\;2ab + b^2$

Let’s discuss the steps to solving radical equations with two cases.

I. Solving Radical Equation With One Radical

II. Solving Radical Equations with Two Radicals 

Solving Radical Equation with One Radical

Step 1: Isolate the radical symbol on one side of the equation.

Step 2: Eliminate the radical symbol by raising both sides of the equation to the power of the index. If it is a square root, then square both sides; if it is a cube root, cube both sides; and so on.

Step 3: Solve the obtained equation using the following formula:

For $x \gt 0$, we have $(^n\sqrt{x})^n = x$

Step 4: Verify by substituting the answer in the original equation.

(Note: The principal square root of a number can only be positive. A radical sign indicates a positive root. So, an equation will not have a solution if its radical has an even index equal to a negative number.)

Example: Solve $\sqrt{2x + 3} \;-\; 5 = 0$.

Step 1: Isolate the radical symbol. 

Add 5 on both sides. Use the addition property of equality.

$\sqrt{2x + 3} = 5$

Step 2: Eliminate the radical symbol. 

To eliminate the radicals, square both sides.

$(\sqrt{2x + 3})^2 = 5^2$

$\Rightarrow 2x + 3 = 25$

Step 3: Solve the obtained equation.

$2x = 25\;-\;3 = 22$

$\Rightarrow x = \frac{22}{2} = 11$

Step 4: Verify the answer. 

Substitute $x = 11$ in the given equation, we get

L.H.S. $= \sqrt{2 \times 11 + 3} \;-\; 5 = \sqrt{25} \;-\; 5 = 5 \;-\; 5 = 0 =$ R.H.S.

Hence, $x = 11$ is the solution of the given equation.

Solving Radical Equations with Two Radicals

If there are two in the radical equation, we begin by isolating one of the two radicals. Isolating the more complicated radical first often works best.

Step 1: Isolate one of the radical terms on one side of the equation.

Step 2: Eliminate the radicals by raising both sides of the equation to the power of the index. This means that if it is a square root, then square both sides; if it is a cube root, cube both sides; etc.

Step 3: Solve the obtained equation once the radical signs are eliminated.

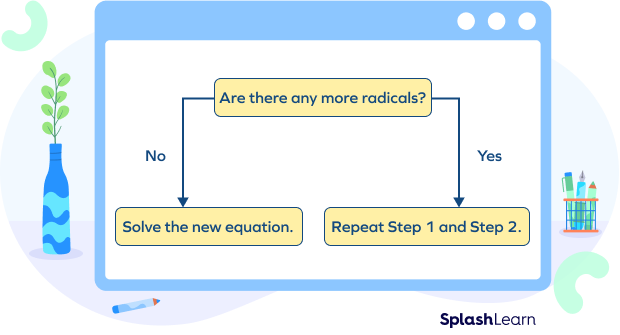
Step 4: Verify the answer in the original equation and check whether it is satisfying or not.

Let’s use this concept to solve an example.

Example: Solve $\sqrt{x + 5} \;-\; \sqrt{x} = 2$.

Step 1: Isolate one of the radical terms on one side of the equation.

$\sqrt{x + 5} = 2 + \sqrt{x}$

Step 2: Eliminate the radicals.

To eliminate the radicals, square both sides.

We get

$(\sqrt{x+5})^2 = (2 + \sqrt{x})^2$

$\Rightarrow x + 5 = 4 + 4 \sqrt{x} + x$ 

Step 3: Solve the obtained equation.

$\Rightarrow 1 = 4 \sqrt{x}$ 

Since a radical is still present in the obtained equation, square both sides again.

$1 = 16x$

$x = \frac{1}{16}$

Step 4: Verify the answer. 

Substitute x=116 in the given equation, and we get

L.H.S. $\sqrt{\frac{1}{16} + 5} \;-\; \sqrt{\frac{1}{16}} = \sqrt{\frac{81}{16}}\;-\; \sqrt{\frac{1}{16}} = \frac{9}{4}\;-\; \frac{1}{4}=2 =$ R.H.S.

Hence, $x = \frac{1}{16}$ is the solution of the given equation.

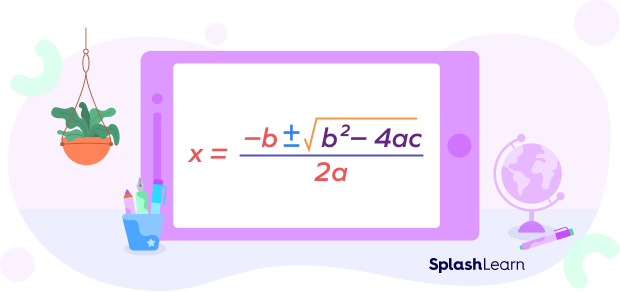
Note: A quadratic equation of the form $ax^2 + bx + c = 0$ obtained in the process of solving a radical equation can also be solved using the quadratic formula.

Facts about Radical Equations

• The modern radical sign, “√” was first introduced by a German mathematician Christoff Rudolff.

• European paper sizes are a good illustration of how a radical is used in the real world. The measurements of an A4-sized sheet of paper are $8.27 \times 11.67$ inches. The ratio of the lengths of the longer and shorter side of an A4 paper is approximately $\sqrt{2}$.

• When you square a radical equation, you sometimes get solutions to the squared equation which may not satisfy the original equation. Such a solution is called an extraneous solution. Thus, if you raise both sides of an equation by some power, then you have to verify your solutions to eliminate the extraneous solutions. 

Conclusion

In this article, we have discussed the radicals, methods, and steps for solving radical equations. Let’s solve a few examples and practice problems.

Solved Examples on Radical Equations

1. Solve $\sqrt{3x^2\;-\;12x} = 6$.

Solution:

Given, $\sqrt{3x^2\;-\;12x} =6$

To eliminate the radical sign, square both sides.

$\bigg(\sqrt{3x^2\;-\;12x}\bigg)^2 = 6^2$

$\Rightarrow 3x^2\;-\;12x = 36$

$\Rightarrow 3x^2\;-\;12x\;-\;36 = 0$

$\Rightarrow 3(x^2\;-\;4x\;-\;12) = 0$

$\Rightarrow x^2\;-\;4x\;-\;12 = 0$

$\Rightarrow x^2\;-\;6x + 2x\;-\;12 = 0$

$\Rightarrow x(x\;-\;6) + 2(x\;-\;6) = 0$

$\Rightarrow (x + 2) (x\;-\;6)=0$

$x=\;-\;2,\; 6$

Verification: 

For $x = \;-2$

L.H.S. $\sqrt{3(\;-\;2)^2\;-\;12(\;-\;2)} = \sqrt{12+24} = \sqrt{36} = 6 =$ R.H.S.

For $x = 6$

L.H.S. $= \sqrt{3(6)^2\;-\;12(6)} = \sqrt{108\;-\;72} = \sqrt{36} = 6 =$ R.H.S.

Hence, the solution of the given equation is $x = \;-\;2,\; 6$.

2. Solve:  $^3sqrt{x\;-\;1} = 3$.

Solution:

$^3\sqrt{x\;-\;1} = 3$

To eliminate the radical, cube both sides.

$(^3\sqrt{x\;-\;1})^3 = 3^3$

$\Rightarrow x\;-\;1 = 27$

$x = 28$

Verification: 

For $x = 28$

L.H.S. $= ^3\sqrt{x\;-\;1} = ^3\sqrt{28\;-\;1} = ^3\sqrt{27} = 3 =$ R.H.S.

Hence, the solution of the given equation is $x = 28$.

3. Solve $^3\sqrt{2x + 4} + 8 = 4$.

Solution:

Given, $^3\sqrt{2x + 4} + 8 = \;-4$

Here, the radical is not isolated, so first isolate the radical on one side.

$^3\sqrt{2x + 4} =\; -4$

To eliminate the radicals, cube both sides.

We get

$(^3\sqrt{2x+4})^3 =(-4)^3$

$\Rightarrow 2x + 4 =\; -64$

$\Rightarrow 2x = \;-64\;-\;4$

$\Rightarrow 2x= \;-68$

$\Rightarrow x = \frac{-68}{2} =\; -34$

Verification:

For $x = \;-34$

L.H.S. $= ^3\sqrt{2(\;-\;34)+4} + 8 = ^3\sqrt{\;-\;68+4} + 8 = ^3\sqrt{\;-\;64} + 8= \;-4 + 8 = 4 =$ R.H.S.

Hence, the solution of the given equation is $x = \;-34$.

4. Solve $\sqrt{x\;-\;2} + \sqrt{x\;-\;1} = 1$.

Solution:

Given, $\sqrt{x\;-\;2} + \sqrt{x\;-\;1} = 1$

Here, the radical is not isolated, so first isolate the radical on one side.

$\sqrt{x \;-\; 2} = 1\;-\; \sqrt{x\;-\;1}$

To eliminate the radicals, square both sides.

We get

$(\sqrt{x-2})^2 = (1-\sqrt{x\;-\;1})^2$

$\Rightarrow x\;-\;2 = 1\;-\;2 \sqrt{x\;-\;1} + x\;-\;1$

$\Rightarrow \;-\;2 = \;-\;2\sqrt{x\;-\;1}$

$\Rightarrow 1 = \sqrt{x\;-\;1}$

Squaring both sides again, we get

$1 = x\;-\;1$

$x = 2$

Verification: 

For $x = 2$

L.H.S. $= \sqrt{x\;-\;2} + \sqrt{x\;-\;1} = \sqrt{2\;-\;2} + \sqrt{2\;-\;1} = 0 + 1 = 1 =$ R.H.S.

Hence, the solution of the given equation is $x = 2$.

5. $\sqrt{x + 4} =x \;-\; 2$

Solution: 

$sqrt{x + 4} = x – 2$

Squaring both sides:

$x + 4 = (x\;-\;2)^2$

$x + 4 = x^2\;-\;4x + 4$

$x^2\;-\;5x = 0$

$x (x\;-\;5) = 0$

$x = 0 ; x = 5$

Verification:

Put $x = 0$

L.H.S. $= \sqrt{0+4} = \sqrt{4} = 2$ 

R.H.S. $= 0 \;-\; 2 $

L.H.S. $\neq$ R.H.S.

Thus, $x = 0$ is not the solution.

Put $x = 5$

L.H.S. $= \sqrt{5 + 4} = \sqrt{9} = 3$

R.H.S. $= 5\;-\;2 = 3$

L.H.S. $=$ R.H.S.

Thus, $x = 5$ is the solution.

Practice Problems on Radical Equations

Frequently Asked Questions about Radical Equations