Repeating Decimal to Fraction: Definition, Steps, Tricks, Examples

What Is Repeating Decimal to Fraction Conversion?

Repeating decimal to fraction conversion is used to express a repeating or recurring decimal in the form of a fraction.

To convert a “terminating decimal” to a fraction, we simply count the number of digits after the decimal point (which are finite); then, we multiply and divide by the appropriate power of ten. 

Example: $0.75 = 0.75 \times \frac{100}{100} = \frac{75}{100} = \frac{3}{4}$   

This is pretty simple, isn’t it? But what about repeating decimals where we cannot count the number of digits after the decimal point? 

A repeating decimal (or a recurring decimal) is a decimal number in which a single digit or a group of digits after the decimal point is repeated infinitely. 

Examples of repeating decimals: 

• $0.4545454545… = 0.\overline{45}$
• $2.333333… = 2.\overline{3}$
• $14.35353535… = 14.\overline{35}$

So, how to write a repeating decimal as a fraction? Let’s find out!

How to Convert Repeating Decimal to Fraction

Repeating or Recurring decimals have a repetitive pattern in the digits after the decimal point. With repeating decimals, it is not possible to count the number of decimal places as it is infinite. So, we follow simple steps to convert repeating decimals to fractions. 

Single Repeating Digit

Example: Convert 0.33333… to a fraction.

Step 1: Identify the repeating digits and the number of repeating digits in the given decimal number. 

Here, the repeating digit is 3.

Number of repeating digits $= 1$

Step 2: Equate the decimal number to some variable. 

Here, we assume $x = 0.3333…$  …(1)

Step 3: First ensure that only the repeating digits come after the decimal point. Then

multiply both the sides of the equation by a power of ten equal to the number of repeating digits.

$x = 0.3333…$

$10x = 10 \times 0.3333…$

Here, after multiplying 0.3333… with 10, the decimal point will shift one position to the right. 

$10x = 3.3333…$ …(2)

Step 4: We subtract the equation (1) from the equation (2). In this case, we get 

$10x \;-\; x = 3.3333… \;- \;0.3333…$

$9x = 3$

Step 5: Simplify to get the answer. 

In this case, we get $x = \frac{3}{9} = \frac{1}{3}$

Multiple Repeating Digits

Now, let us convert a multi-digit repeating decimal to a fraction. 

Example: Convert 5.232323… to a fraction.

Step 1: The repeating digits in the given decimal number are 23.

The number of repeating digits $= 2$

Step 2: Let $x = 5.232323…$

Step 3: There are two repeating digits. Multiply the above equation by $10^2 = 100$. 

We will get 

$100x = 10 \times 0 5.232323…$

Shift the decimal point two places to the right. 

$100x = 523.232323…$

Step 4: Subtract $x = 5.232323….$ from $100x = 523.232323…$

We will get $99x = 518$

Step 5: $x = \frac{518}{99}$ 

Non-Repeating Digits Followed by Repeating Digits

Example: Convert 7.324242… to a fraction.

Step 1: Repeating digits $= 42$

Note that 3 is not repeating.

Step 2: Let $x = 7.3424242…$

Let’s first shift the non-repeating digit 3 to the left side of the decimal point by multiplying both sides by 10.

In this case, we get $10x = 73.424242…$ – (1)

Step 3: Multiply both the sides by the power of 10 equal to the number of repeating digits. 

In this case, we get $100x = 7342.424242…$ – (2)

Step 4: Subtracting (1) from (2), we get 

$1000x \;-\; 10x = 7342.424242… \;-\; 73.424242…$

$\Rightarrow 990x = 7269$

$\Rightarrow x = \frac{7269}{990} = \frac{2423}{330}$

Repeating Decimal to Fraction: Tricks

There is an easy trick to convert a repeating decimal to the fraction form. Write the repeating digits as the numerator over the same number of 9s. 

Repeating Decimal of the Form $0.\overline{pqrs}$

This trick is applicable only for repeating decimals having only repeating digits after the decimal point. 

We can write a formula to convert such decimals to fractions as

$0.\overline{pqrs} = \frac{Repeated\; digit\; or\; digits}{Number\; of\; 9’s\; Equal\; to\; the\; Number\; of\; Repeated\; Digits} $

Converting a fraction to a repeating decimal examples based on this trick:

Example 1: $0.2222… = \frac{2}{9}$ 

There is only 1 repeating digit, 2. So, the denominator will be 9.

Example 2: $0.323232… = \frac{32}{99}$

There are 2 repeating digits, 3 and 2. So, the numerator will be 32, and two 9’s or 99 will come in the denominator.

Example 3: $0.999… = \frac{9}{9} = 1$

Repeating Decimal of the Form $0.pq…\overline{rs}$

Here, the decimal consists of some non-repeating digits followed by the repeating digits.

The formula to convert such decimals to fractions is

$0.pq…\overline{rs} = \frac{pqrs \;-\; pq}{No.\; of\; 9’s\; equal\; to\; repeating\; terms\; followed\; by\; no.\; of\; 0’s\; equal\; to\; non‒repeating\; terms}$

Converting a fraction to a repeating decimal examples based on this trick:

Example 1: 0.12757575…

$0.12757575… = \frac{1275 \;-\; 12}{9900} = \frac{1263}{9900}$

Example 2: $0.00345345… = 0.00\overline{345}$

$0.00\overline{345} = \frac{345 – 00}{99900} = \frac{345}{99900}$

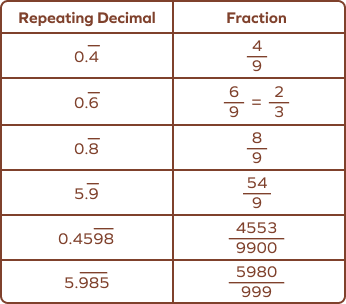
Repeating Decimal to Fraction Chart

The chart given below will help to convert some repeating decimals to a fraction. 

Facts about Repeating Decimal to Fraction

Rational numbers are of the form $pq; q \neq 0, p$ and $q$ are integers. Repeating decimals are considered as rational numbers since any repeating decimal can always be written in the form of a fraction.  

Example: $0.5555… = 0.\overline{5} = \frac{5}{9}$

Solved Examples of Repeating Decimal to Fraction

1. Convert 1.8888… to fraction.

Solution: 

Let $x = 1.8888…$ — (1)

Multiplying both the sides by 10, we get

$10x = 18.8888…$ — (2)

Subtracting (1) from (2), we get

$10x \;-\; x = 18.888…\;-\;1.888…$

$9x = 17$

$x = \frac{17}{9}$

2. What fraction is equivalent to the repeating decimal number 0.434343…?

Solution: 

Let $x=0.434343…$ — (1)

Multiplying both the sides by 100, we get

$100x = 43.434343….$ — (2)

Subtracting (1) from (2), we get

$100x\;-\;x = 43.4343…\;-\;0.4343…$

$99x = 43$

$x = \frac{43}{99}$

3. Convert 0.567567567… to fraction.

Solution: 

Let $x = 0.567567567…..$ — (1)

Multiplying both the sides by 1000, we get

$1000x = 567.567567….$ — (2)

Subtracting (1) from (2), we get

$1000x \;-\; x = 567.567567567…\;-\;0.567567567…$

$999x = 567$

$x = \frac{567}{999} = \frac{189}{333} = \frac{63}{111} = \frac{21}{37}$

4. Which fraction is equivalent to 2.34444…?

Solution: 

Let $x = 2.34444…$ 

Multiply both the sides by 10 so that all the repeating digits come after the decimal point.

$10x = 23.4444…$ — (1)

Multiplying both sides by 10 

$100x = 234.4444…$ — (2)

Subtracting (1) from (2), we get

$100x\;-\;10x = 234.444…\;-\;23.444…$

$90x = 211$

$x = \frac{21}{190}$

5. What fraction is equivalent to the repeating decimal number 24.579579…? 

Solution: 

Let $x = 24.579579…$ — (1)

Multiplying both the sides by 1000

$1000x = 24579.579579…$ — (2)

Subtracting (1) from (2), we get

$1000x \;-\; x = 24579.579579… \;-\; 24.579579…$

$999x = 24555$

$x = \frac{24555}{999} = \frac{8185}{333}$

Practice Problems on Repeating Decimal to Fraction

Frequently Asked Questions on Repeating Decimal to Fraction