Row Matrix: Definition, Formula, Properties, Facts, Examples

What Is a Row Matrix?

A row matrix is a type of a matrix that has only one row. 

The total number of columns in a row matrix is the total number of elements that make up the single row. 

The row matrix is not a square matrix as the number of rows is not equal to the number of columns. Thus, we cannot find the determinant of a row matrix.

Examples of a row matrix: 

A_{1 x 3} $= \left[7  \;5  \;6\right]$

B_{1 x 4} $= \left[10 \; 22 \; 63 \; 12\right]$

Definition of Row Matrix

A row matrix is a matrix of an order $1 \times n$, where n is the number of columns. 

A row matrix can be expressed in mathematical form as:

A = [a₁₁  a₁₂  a₁₃ ……. a₁ₙ]_{1 x n}

where,

a₁₁ , a₁₂ , a₁₃ ,……., a₁ₙ are the elements 

$n =$ number of columns 

Order of a Row Matrix

The order of a row matrix is $1 \times n$, where 1 represents the number of rows and n is the number of columns.

Transpose of a Row Matrix

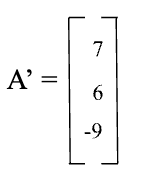
The transpose of a row matrix of order $1 \times n$ is a column matrix of order $n \times 1$. It is obtained by interchanging the row by a column. Transpose of a matrix A is denoted by A’ or A^T.

Example: The transpose of the row matrix $A = \left[ 7  \;6 \;-\;9\right]$ is 

Properties of Row Matrix

1. There is only one row in a row matrix.
2. The total number of columns in a matrix equals the total number of elements in the row.
3. A row matrix is a type of a rectangular matrix.
4. A transpose of a row matrix with order $1 \times n$ is a column matrix with order $n \times 1$.
5. The row matrix can only be added to (or subtracted from) another row matrix with the same order.
6. A row matrix with order $1 \times n$ can only be multiplied by a column matrix of order $n \times 1$.
7. A singleton matrix (matrix of order $1 \times 1$ which has only one element) is produced when a row matrix and a column matrix are multiplied.

Row Matrix Operations

We can perform simple arithmetic operations across a row matrix, such as addition, subtraction, multiplication, and division. 

We can only add or subtract row matrices of the same order. To add/subtract two or more matrices, we add/subtract the corresponding elements.  

Example: 

$A = \left[3  9  8\right]$ and $B = \left[5 \; 1 \; 7\right]$

$A + B = \left[3 + 5  \; 9 + 1  \; 8 + 7\right] = \left[8  \; 10   \;15\right]$

$A \;-\; B = \left[3 \;-\; 5 \; 9 \;-\; 1 \; 8 \;-\; 7\right] = \left[\;-\;2  \; 8  \; 1\right]$

We can multiply a row matrix with a column matrix. We can multiply a row matrix of order $1 \times n$ only with a column matrix of order $n \times 1$. The result of the multiplication of a row and a column matrix is a singleton matrix. 

Example: 

Let us consider matrix $A = \left[2 \; 5  \;3\right]$ and  

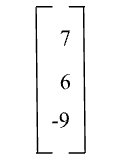
matrix B =

$A \times B = \left[(2 \times 7) + (5 \times 6) + (3\times -9)\right]$

$A \times B = \left[14 + 30 \;-\; 27\right]$

$A \times B = \left[44 \;-\; 27\right]$

$A \times B = \left[17\right]$

Types of Matrices

There are ten different kinds of matrices. They are as follows:

1. Row matrix: A matrix that has only one row.
2. Column matrix: A matrix which contains only one column.
3. Diagonal matrix: A square matrix that has 0 as the element on the leading diagonals.
4. Scalar matrix: This kind of matrix has the same elements on the diagonal.
5. Square matrix: This type of matrix has the same number of rows and columns.
6. Identity matrix: It is also known as a unit matrix. A matrix with all the diagonal elements equal to 1.
7. Zero matrix: All the elements of this matrix are zero. It is also called a null matrix.
8. Triangular matrix: In this matrix, all the elements above or below the matrix leading diagonal are zero. There are two types of triangular matrix: upper triangular matrix and lower triangular matrix.
9. Symmetric matrix: A square matrix [aᵢⱼ] is a symmetric matrix when $a_{ij} = a_{ji}$.
10. Skew symmetric matrix: A skew-symmetric matrix is the kind of square matrix [aᵢⱼ] when $a_{ij} = \;-\;a_{ji}$. The elements of the leading diagonal of this matrix are 0.

Facts about Row Matrices

Conclusion

In this article, we learned about row matrices, their properties and also discussed operations on row matrices. Let’s use the concepts we learned to solve a few examples and practice problems.  

Solved Examples on Row Matrix

1. Find the sum of the row matrices $A = \left[4 \; 10 \; 11\right]$ and B $= \left[6\;  5 \; 20\right]$.

Solution: The given matrices are

$A = \left[4  \;10\;  11\right]$ 

$B = \left[6 \; 5 \; 20\right]$

$A + B = \left[4\;  10  \;11] + [6  \;5  \;20\right]$

$A + B = \left[4 + 6 \;  10 + 5 \;  11 + 20\right]$

$A + B = \left[10\;  15  \;31\right]$

Therefore, the resultant matrix $A + B = \left[10 \; 15\;  31\right]$.

2. Subtract matrix $B = \left[31 \; 25\;  16\right]$ from matrix $A = \left[47 \; 25 \; 34\right]$. 

Solution: The given matrices are: 

$B = \left[31 \; 25 \; 16\right]$

$A = \left[47 \; 25 \; 34\right]$

$A \;-\; B = \left[47  25 \; 34\right] \;-\; \left[31  \;25 \; 16\right]$

$A \;-\; B = \left[47\;-\;31 \; 25\;-\;25 \; 31\;-\;16\right]$

$A \;-; B = \left[16\;  0 \; 15\right]$

Therefore, the resultant matrix would be $A \;-\; B = \left[16\;  0  \;15\right]$

3. Find the product of the following matrices $A = \left[2 \; 6  \;7  \;-\;5\right]$ and B =

Solution: The given matrices are

$A = \left[2 \; 6  \;7  \;-\;5\right]$ 

B =

$A \times B =  \left[(2 \times 3) + (\;-\;5 \times 6) + (7 \times 4) + (\;-\;5 \times \;-\;1)\right]$ 

$A \times B =  \left[6 \;-\; 30 + 28 + 5\right]$ 

$A \times B = \left[39 \;-\; 30\right]$

$A \times B = \left[9\right]$

Therefore, the product of the matrices is $A \times B = \left[9\right]$.

Practice Problems on Row Matrix

Frequently Asked Questions about Row Matrix