Volume of a Rectangular Prism – Definition with Examples

You see it in boxes as you grab a tissue or pop open your box of cereal. You see it in books as you remove your bookmarks to begin reading. You see it in laptops as you finish typing your latest assignment. 

Yes, we are talking about the rectangular prism.

What Is a Rectangular Prism?

A rectangular prism is a three-dimensional shape with six faces. All the faces (top, bottom, and lateral faces) of the prism are rectangular so that all the pairs of opposite faces are congruent. It is also known as a cuboid. In short, a rectangular prism has four rectangular faces and two parallel rectangular bases. 

How is a rectangular prism different from a rectangle? 

To begin with, why is it important to know the difference between different types of shapes? 

Every shape has distinct properties and these properties help to know quantities such as volume, surface area, etc. Remember, you would not know to not put a rectangle on top of a triangle if you don’t know how they are different. 

Difference Between Rectangle & Rectangular Prism

Rectangle	Rectangular Prism
It is a 2D shape.	It is a 3D shape.
It has four sides.	It has six faces, eight verticals & twelve edges.
It is made of four sides with the opposite sides having equal lengths.	It is made up of six rectangles put together.
It has width and length.	It has width, height and length.
It is made of two pairs of lines.	It is made of three pairs of rectangles.

Now that we know what rectangular prisms are, let’s look at how we can calculate its volume.

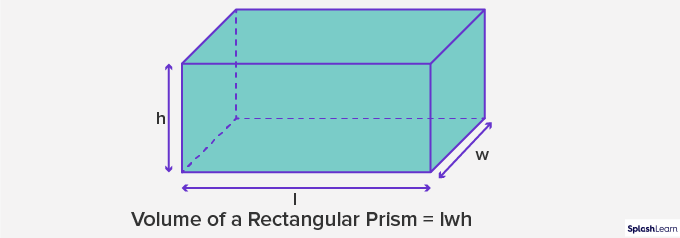
The Formula for Volume of a Rectangular Prism

By multiplying the base area of a prism by its height, you will get the volume of a prism. That is to say, the volume of a prism = base area × height.

Since a rectangular prism’s base is a rectangle itself, the volume of a rectangular prism, by applying the formula given above, will be:

Volume of a rectangular prism (V) = l × w × h

Where,

“l” means the base length, and

“w” means the base width,

“h” means the height

Solved Examples

Example 1: Find out the volume of a rectangular prism with base length 9 inches, base width 6 inches, and height 18 inches, respectively.

Solution:

Here,

Length (l) = 9 inches

Width (b) = 6 inches

Height (h) = 18 inches

So, the volume of the given rectangular prism = l × w × h = 9 × 6 × 18 = 972 cubic inches.

Example 2: Find out the height of a rectangular prism whose base area is 20 sq. units and a volume is 60 cubic units.

Solution:

Given is the base area of the rectangular prism = 20 sq. units

And the volume of the rectangular prism = 60 cubic units

Now, applying the volume of the rectangular prism formula, 

base area × height = 60 cubic units.

⇒ 20 × height = 60

⇒ height = 60 ÷ 20 units

⇒ height = 3 units 

Example 3: Find out the base area of a rectangular prism with the help of the given measurements: length = 12 inches, height = 20 inches, and volume = 2,160 cubic inches. 

Solution:

Here,

Length (l) = 12 inches

Height (h) = 20 inches

Volume (V) = 2,160 cubic inches

The volume of the rectangular prism = l × w × h  

⇒ 2,160 = 12 × w × 20 

⇒ 2,160 ÷ (12 × 20) = w

⇒ 9 = w

Therefore, width (w) = 9 inches.

Area = l × w = 12 × 9 = 108 sq. inches.

Conclusion

The volume of a rectangular prism is an important concept for 5th graders to learn. As we have already discussed, the volume of a rectangular prism is the product of its dimensions, i.e., length, width, and height. This can be better understood with practical examples. Using SplashLearn, students can practice each example with online interactive worksheets. This game-based learning app makes learning fun and keeps your child engaged.

Every game on SplashLearn is curriculum-based and scientifically designed. To boost your kid’s knowledge in mathematics and allow them to practice mathematics fearlessly, you can sign up to SplashLearn for free!

Practice Problems

Frequently Asked Questions